力扣34在排序数组中查找元素的第一个和最后一个位置、二分法及相关扩展

二分法是算法中的基础，今天用Python语言来总结一下，有错误的地方希望能被指出。

1、在一个有序数组中，查找某个数是否存在

####二分法查找某数是否存在
def BSExsit(arr,num):     ###arr为数组，num为目标数
    if len(arr) <= 0:
        return False
    l = 0
    r = len(arr) - 1
    m = 0
    while l < r:
        m = l+((r-l)>>1)
        if arr[m] == num:
            return True
        elif arr[m] > num:
            r = m-1       ###大于目标数往左边砍一半
        else:
            l = m+1      ####小于目标数往右边砍一半
    return arr[l] == num  ####判断左位置上的数与目标数是否相同

时间复杂度O(logN)
注：关于中点下标的写法：

2、在一个有序数组中，找>=某个数最左侧的位置

###在一个有序数组中，找>=某个数最左侧的位置
def BSNearLeft(arr,num):
    if len(arr) <= 0:
        return None
    l = 0
    r = len(arr)-1
    m = 0
    while l<r:
        m = l+((r-l)>>1)
        if arr[m] >= num:     ###满足条件往左边砍一半
            index = m         ###记下此时的中间位置
            r = m-1
        else:
            l = m+1          ###不满足条件往右边砍一半
    return index             ###中间位置即为所要找的位置

3、局部最小值

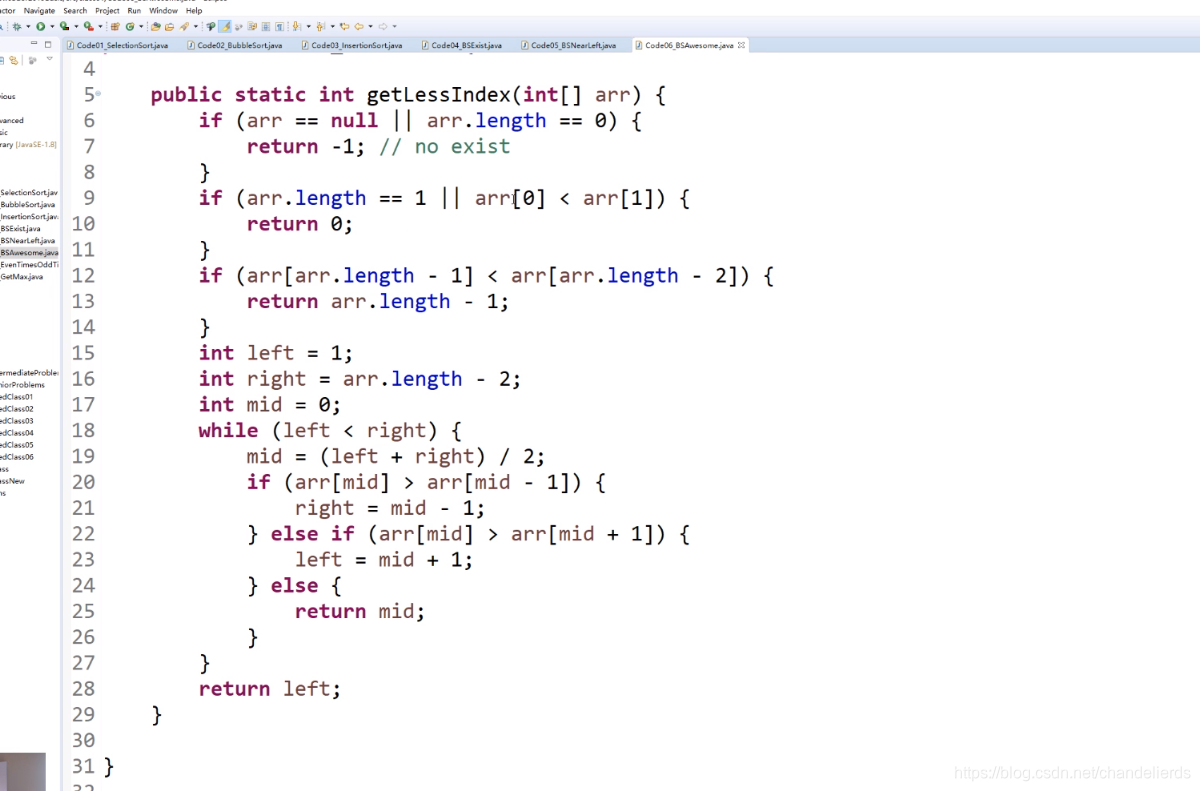
注意：有序不是二分法的必要条件

力扣34

class Solution:
    def searchRange(self, nums: List[int], target: int) -> List[int]:
        res = [-1,-1]
        res[0] = self.binarySearch(nums, target, True)
        res[1] = self.binarySearch(nums, target, False)
        return res
    
    # 二分法寻找左/右边界
    def binarySearch(self, nums, target, search_left):
        n = len(nums)
        l, r = 0, n - 1
        res = -1
        while (l <= r):
            m = l + ((r - l) >>1)
            if target < nums[m]:
                r = m - 1
            elif target > nums[m]:
                l = m + 1
            else:
                res = m
                # 寻找左边界，从右边逼近
                if search_left:
                    r = m - 1
                else:
                    # 寻找右边界，从左边逼近
                    l = m + 1
        return res