机器学习-逻辑回归（LR）

最新推荐文章于 2025-02-13 16:48:16 发布

原创最新推荐文章于 2025-02-13 16:48:16 发布 · 399 阅读

0 ·

CC 4.0 BY-SA版权

本文深入介绍了逻辑回归模型，包括模型定义、权值系数的极大似然估计方法以及使用梯度上升算法进行参数优化的过程。此外，还提供了Python代码示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

逻辑回归模型是一种分类模型，用条件概率分布的形式表示 P(Y|X)P(Y|X)，这里随机变量 X 取值为 n 维实数向量，例如 x=( $x^{\(1)},x^{\(2)}....,x^{\(n)}$ )，Y 取值为0或1。于是就有如下模型定义：

logistic分类器是由一组权值系数组成的，最关键的问题就是如何获取这组权值，通过极大似然函数估计获得，并且 Y~f(x;w)

似然函数是统计模型中参数的函数。给定输出x时，关于参数θ的似然函数L(θ|x)（在数值上）等于给定参数θ后变量X 的概率：L(θ|x)=P(X=x|θ)

那么对于上述m个观测事件，设

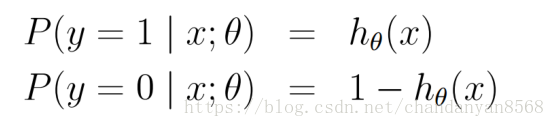
其联合概率密度函数，即似然函数为：

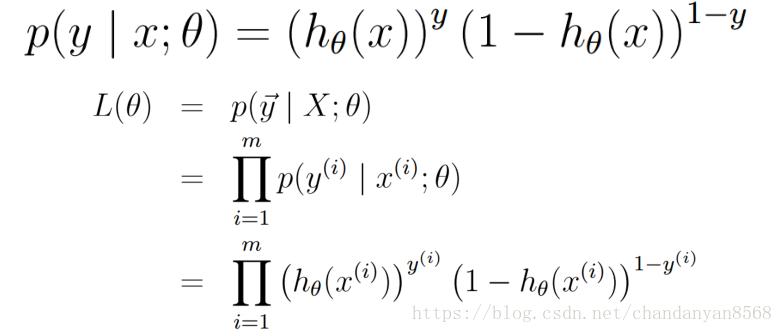
目标：求出使这一似然函数的值最大的参数估，w1,w2,…,wn，使得L(θ)取得最大值。

对L(θ)取对数：

因此优化的目标就是使得l(θ)取极大值，对l(θ)求导有：

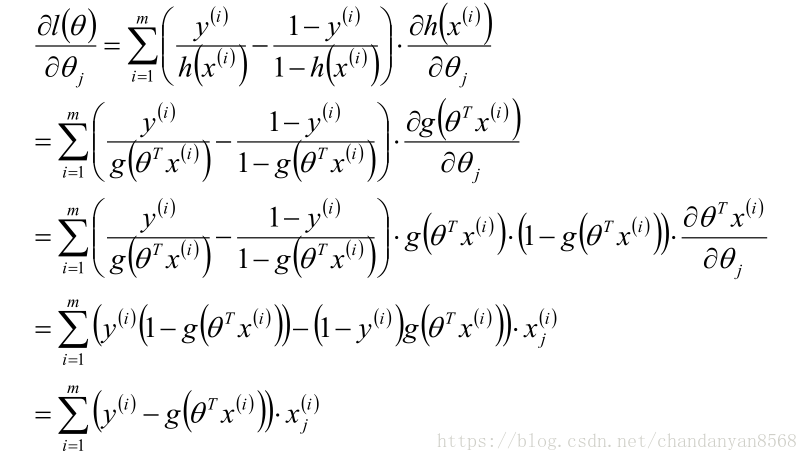
所以学习规则为：

代码实现：

import numpy as np

def sigmoid(inX):
    return 1.0/(1+exp(-inX))

def gradAscent(dataMatIn, classLabels):
    dataMatrix = np.mat(dataMatIn)             #convert to NumPy matrix
    labelMat = np.mat(classLabels).transpose() #convert to NumPy matrix
    m,n = np.shape(dataMatrix)
    alpha = 0.001
    maxCycles = 500
    weights = np.ones((n,1))
    for k in range(maxCycles):              #heavy on matrix operations
        h = sigmoid(dataMatrix*weights)     #matrix mult
        error = (labelMat - h)              #vector subtraction
        weights = weights + alpha * dataMatrix.transpose()* error #matrix mult
    return weights