数据结构学习日志之二十二--普里姆算法

假设在n个城市之间建立通信联络网，则联通n个城市最少需要n-1条线路，最多需要n(n-1)/2条线路，连接两个城市必然需要付出一定的代价，假设有一个连通网，代表n个城市和n个城市间可能设置的通信线路，网的顶点代表n个城市，边代表线路，边上的权值代表需要连接这两个城市付出的代价。对于n个顶点的连通网可以建立许多不同的生成树，那么有一棵树必然是耗费最小代价的，那么这棵树就是最小生成树。

生成最小生成树有两种算法，一种是普里姆（prim）算法，一种是克鲁斯卡尔（kruskal）算法

我们来介绍普里姆算法

此算法可以叫做“加点法”，每次迭代选择代价最小的边的点，加入到最小的生成树种。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

以上图为例: 

1.以a点开始，最小权值为1，另一顶点是c，将c加入到最小生成树中。此时树 a-c

2.在最小生成树的顶点找到一个权值最小且另一顶点不在树中的，最小权值是4，另一顶点是f，将f加入到树里面。此时树为a-c-f

3.重复上一个步骤，a-c-f-d；  a-c-f-d-b;  a-c-f-d-b-e;

实现：

以上图为例，假设初始点为a，把连接A点的线标记为紫线

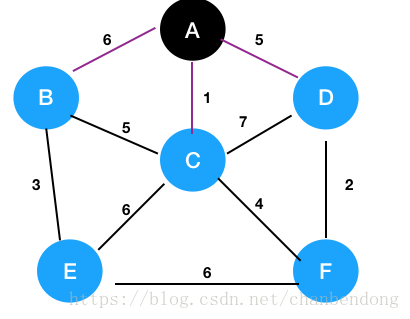
选择权值最小的线涂成红线，相邻顶点涂黑

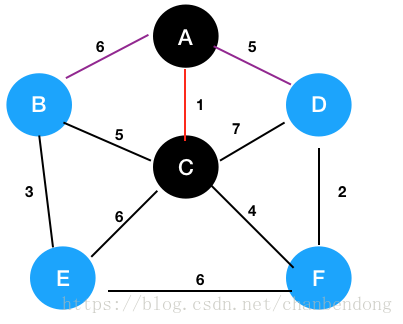
接下来，把黑点与蓝点相连的线都涂成紫色，与两个黑点相连的蓝点取权值小的作为紫线