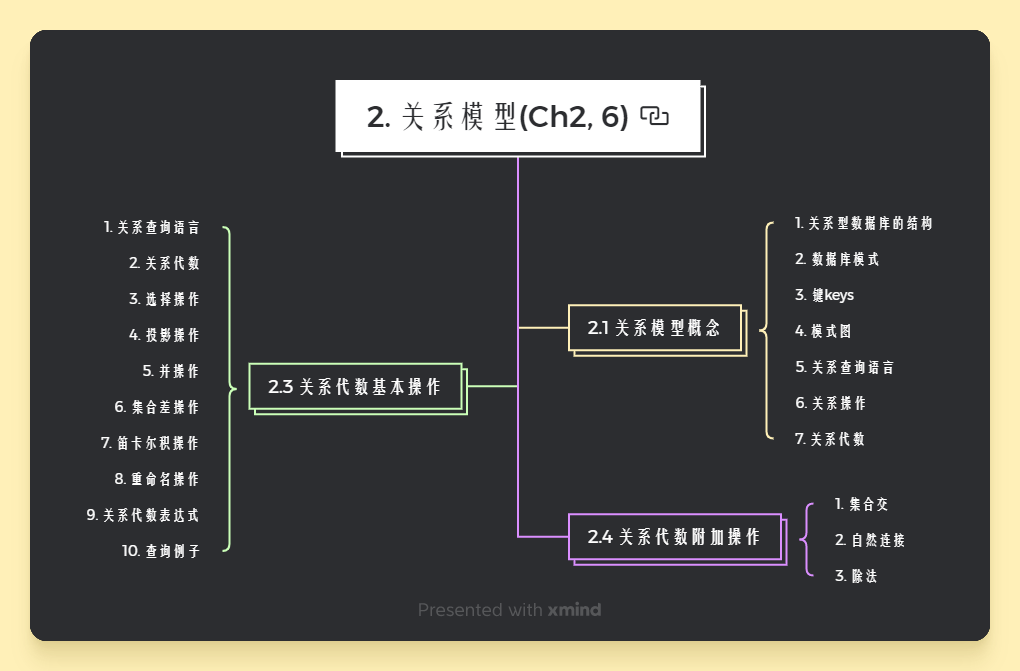
2. 关系模型(Ch2, 6)
这里的一些md语法和语雀不一样,原文来自我的语雀
点击阅读原文,阅读更丝滑:《数据库复习-2. 关系模型(Ch2, 6)》
文章目录
1.关系模型概念
1.1.关系型数据库的结构
- **表:**关系型数据库由一系列表组成,每个表都有一个唯一的名称。表格中的一行代表一组值之间的关系。
- 元组:元组简单来说就是一系列(或列表)的值。$ n 个值之间的关系在数学上由一个 个值之间的关系在数学上由一个 个值之间的关系在数学上由一个 n_tuple 的值来表示,即一个包含 的值来表示,即一个包含 的值来表示,即一个包含 n $个值的元组,它对应于表格中的一行。
- 属性:“属性”指的是表中的一列。
- 关系实例:用于指代关系的一个具体实例,即包含一组特定行的关系。
- 域:属性允许的值,称为该属性的域。
- **原子性:**如果域的元素被视为不可分割的单元,则该域是原子的。要求对于所有关系$ r , , , r $的所有属性的域都必须是原子的。
**null****:**空值是一个特殊的值,表示该值未知或不存在。
1.2.数据库模式
- **数据库模式schema:**数据库的逻辑设计
- **数据库实例instance:**在特定时刻数据库中数据的快照
- 关系模式:关系对应于编程语言中的变量概念,而关系模式对应于编程语言中的类型定义概念。总的来说,关系模式由属性列表及其对应的域组成。
1.3.键keys
- **键:**一种指定如何区分给定关系中元组的方法。这是通过它们的属性来表达的。也就是说,元组的属性值必须是能够唯一识别该元组的值。
- **超键superkey:**超键是由一个或多个属性组成的集合,这些属性共同允许我们唯一地识别关系中的一个元组。
- **候选键candidate keys:**如果$ K 是一个超键,那么 是一个超键,那么 是一个超键,那么 K $的任何超集也是一个超键。没有任何真子集是最小超键,被称为候选键。
- **主键primary key:**指代被选为区分关系中元组的候选键,唯一。
- 外键foreign key:一个关系$ r_1 ,可能在其属性中包括另一个关系 ,可能在其属性中包括另一个关系 ,可能在其属性中包括另一个关系 r_2 的主键。这个属性被称为 的主键。这个属性被称为 的主键。这个属性被称为 r_1 的 ∗ ∗ 外键 ∗ ∗ ,引用 的**外键**,引用 的∗∗外键∗∗,引用 r_2 。关系 。关系 。关系 r_1 也被称为 ∗ ∗ 外键依赖的引用关系 ∗ ∗ ,而 也被称为**外键依赖的引用关系**,而 也被称为∗∗外键依赖的引用关系∗∗,而 r_2 $被称为外键的被引用关系。
- 引用完整性约束:引用完整性约束要求在引用关系中的任何元组的指定属性中出现的值,也必须出现在被引用关系中的至少一个元组的指定属性中。
1.4.模式图
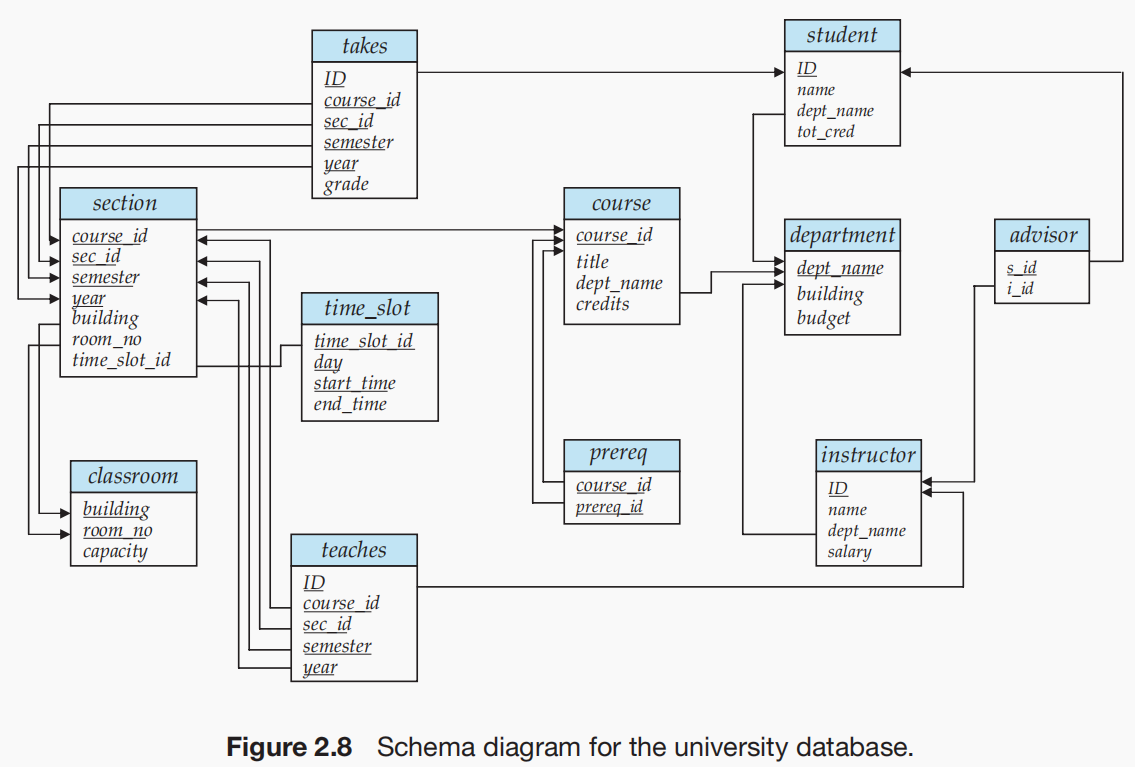
- **模式图:**数据库模式,连同主键和外键依赖关系,可以通过模式图来表示。
- 每个关系都显示为一个框,顶部以蓝色显示关系名称,框内列出了属性。
- 主键属性以下划线表示。
- 外键依赖关系显示为从引用关系的外键属性指向被引用关系的主键的箭头。
1.5.关系查询语言
- **查询语言:**是一种用户从数据库中请求信息的语言。
- 过程式语言:用户指导系统对数据库执行一系列操作来计算所需的结果。
- 非过程式语言:用户描述所需的信息,而不提供获取该信息的具体程序。
1.6.关系操作
- **关系操作:**一组可以应用于单个关系或一对关系的操作,操作的结果是一个单一的关系。具体来说,关系查询的结果本身就是一个关系,所以关系操作可以应用于查询的结果,也可以应用于给定的关系集。
1.7.关系代数
- 关系代数定义了一组在关系上的操作,与通常的代数操作如加法、减法或乘法类似。
- 关系代数运算通常接受一个或两个关系作为输入,并返回一个关系作为输出。
2. 关系代数基本操作
2.1.关系代数
| 符号 (名称) | 定义 | 描述 | 使用示例 | 图示 |
|---|---|---|---|---|
| $ σ_p® $ (选择Select) | $ σ p ( r ) = { t ∈ r and p ( t ) } σ_p(r) = \{t ∈ r \ \text{and} \ p(t)\} σp(r)={t∈r and p(t)} , , , p 为选择谓词: < b r / > ‘ < a t t r i b u t e > o p < a t t r i b u t e > o r < c o n s t a n t > ‘ , < b r / > ‘ o p ‘ 为 为选择谓词:<br/>`<attribute> op <attribute> or <constant>`,<br/>`op`为 为选择谓词:<br/>‘<attribute>op<attribute>or<constant>‘,<br/>‘op‘为 = , ≠ , > , > . < . ≤ =, ≠, >, >. <. ≤ =,=,>,>.<.≤ , < b r / > ,<br/> ,<br/> p 可以用 可以用 可以用 n o t ¬ a n d ∧ o r ∨ not\neg \ and\land \ or\vee not¬ and∧ or∨ $ 连接 | 返回满足谓词条件的输入关系的行。 | $ σ s a l a r y ≥ 85000 ( instructor ) σ_{salary \geq 85000}(\text{instructor}) σsalary≥85000(instructor) < b r / > <br/> <br/> KaTeX parse error: Expected 'EOF', got '_' at position 14: σ_{\text{dept_̲name="Physics"}… $ | 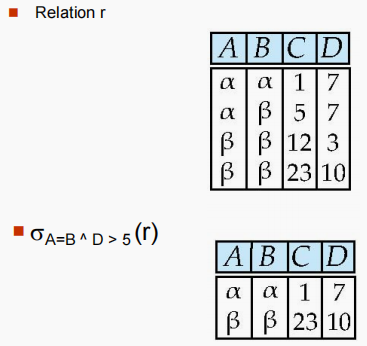 |
| $ Π $ (投影Project) | $ Π A 1 , A 2 , . . . , A k ( r ) Π_{A_1,A_2,...,A_k}(r) ΠA1,A2,...,Ak(r) $ | 输出输入关系中所有行的指定属性,并移除重复的元组。 | $ Π ID, salary ( instructor ) Π_{\text{ID, salary}}(\text{instructor}) ΠID, salary(instructor) $ | 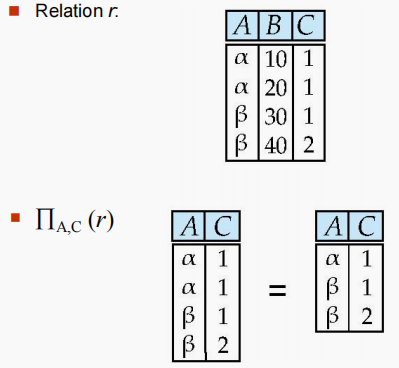 |
| $ ∪ $ (并集union) | $ $r ∪ s = {t | t ∈ r \ \text{or} \ t ∈ s}$ $ | 输出两个输入关系的元组并集。 | $ Π name ( instructor ) ∪ Π name ( student ) Π_{\text{name}}(\text{instructor}) ∪ Π_{\text{name}}(\text{student}) Πname(instructor)∪Πname(student) $ |
| $ - $ (集合差set difference) | $ $r - s = {t | t ∈ r \ \text{and} \ t ∉ s}$ $ | 输出属于第一个关系但不属于第二个关系的元组。 | $ Π name ( instructor ) − Π name ( student ) Π_{\text{name}}(\text{instructor}) - Π_{\text{name}}(\text{student}) Πname(instructor)−Πname(student) $ |
| $ × $ (笛卡尔积Cartesian product) | $ $r × s = {t \ q | t ∈ r \ \text{and} \ q ∈ s}$ $ | 输出两个输入关系的所有行对(无论是否具有相同的公共属性)。 | $ instructor × department \text{instructor} × \text{department} instructor×department $ |
| $ ρ_{x}E $(重命名rename) | $ ρ x ( A 1 , A 2 , . . . , A n ) ( E ) ρ_{x(A_1, A_2, ..., A_n)}(E) ρx(A1,A2,...,An)(E) $ | 重命名关系的名称(或属性名)。 | $ ρ s ( r ) ρ_s(r) ρs(r) $ | 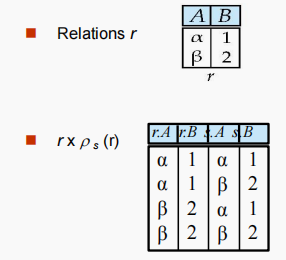 |
2.2. 关系代数表达式
设 E₁ 和 E₂ 是关系代数表达式。以下关系代数表达式均有效:
- E₁ ∪ E₂ (并集操作)
- E₁ − E₂ (集合差操作)
- E₁ × E₂ (笛卡尔积操作)
- σₚ(E₁),其中 p 是作用于 E₁ 中属性的谓词(选择操作)。
- Πₛ(E₁),其中 S 是由 E₁ 中某些属性组成的列表(投影操作)。
- ρₓ(E₁),其中 x 是 E₁ 结果的新名称(重命名操作)。
3. 关系代数附加操作
| 符号 (名称) | 定义 | 描述 | 使用示例 | 图示 |
|---|---|---|---|---|
| $ r ∩ s $ (集合交) | $ r \cap s = { t | t \in r \ \text{and} \ t \in s } $ | 返回两个集合中共同的元组。 | $ \Pi_{\text{customer_name}} (\text{borrower}) \cap \Pi_{\text{customer_name}} (\text{depositor}) $ |
| $ r \mathop{⋈} \limits _{A \theta B} s ( ( ( \theta\text{-}join $连接操作) | $ R \mathop\bowtie \limits {A\theta B}S={\overbrace{t{\mathrm{r}}t_{\mathrm{s}}} | t_{\mathrm{r}}\in R\wedge t_{\mathrm{s}}\in S\wedge t_{\mathrm{r}}[A] \ \theta \ t_{\mathrm{s}}[B] } $ | 满足$ \theta $条件的连接在一起 | $ R \mathop\bowtie \limits _{C < E}S < b r / > <br/> <br/> R \mathop\bowtie \limits _{A=B}S $ |
| $ r ⋈ s $ (自然连接) | $ \pi_{r.A, r.B, r.C, r.D, s.E}\left(\sigma_{r.B=s.B \ r.D=s.D}\left(r\times s\right)\right) $ | 将两个关系中所有属性名相同的列相匹配的元组连接起来。 | $ \text{r} \bowtie \text{s} $ | 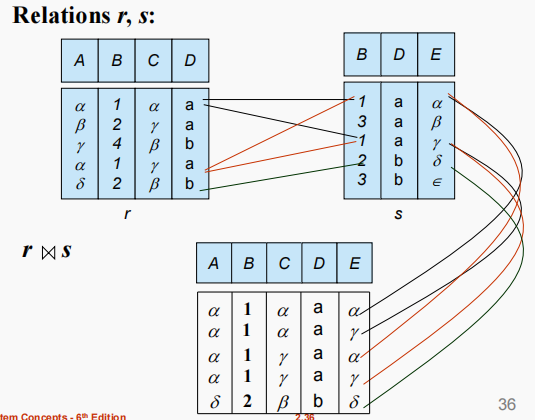 |
| $ r ÷ s $ (除法) | $ r\div s={t\mid t\in\pi_{R-S}®\wedge\forall u\in s\to t_u\in r ) } $ | 返回在 $ r $ 中但不在 $ s $ 中的元组,$ t 中的属性在 中的属性在 中的属性在 R 中但不在 中但不在 中但不在 S 中,用于在 中,用于在 中,用于在 r 中找出那些满足 中找出那些满足 中找出那些满足 s $中所有条件的元组集合。 | $ \text{course} \div \text{prereq} $ | 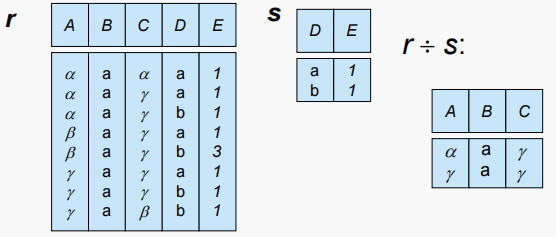 |
- $ join $操作的补充
- $ inner \ join $
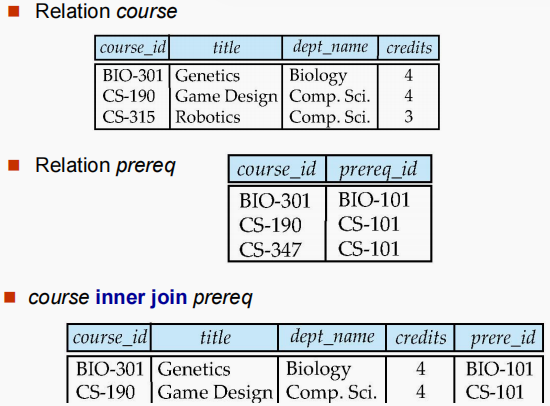
- $ natural \ left \ outer \ join $
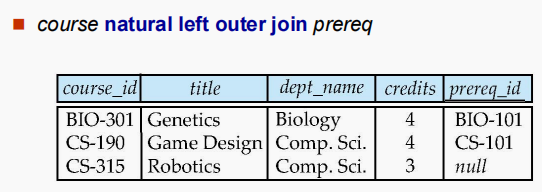
- $ natural \ right \ outer \ join $
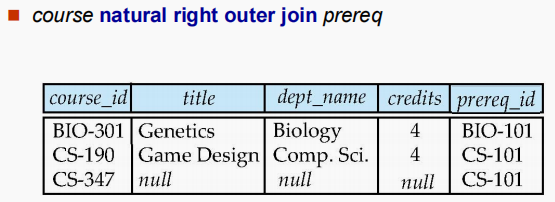
- $ full \ outer \ join $
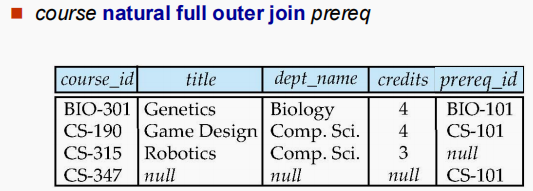





















 3167
3167

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








