pytorch学习2

1、过拟合和欠拟合

训练误差和泛化误差在解释上述现象之前，我们需要区分训练误差（training error）和泛化误差（generalization error）。通俗来讲，前者指模型在训练数据集上表现出的误差，后者指模型在任意一个测试数据样本上表现出的误差的期望，并常常通过测试数据集上的误差来近似。计算训练误差和泛化误差可以使用之前介绍过的损失函数，例如线性回归用到的平方损失函数和softmax回归用到的交叉熵损失函数。机器学习模型应关注降低泛化误差。K折交叉验证由于验证数据集不参与模型训练，当训练数据不够用时，预留大量的验证数据显得太奢侈。一种改善的方法是K折交叉验证（K-fold cross-validation）。在K折交叉验证中，我们把原始训练数据集分割成K个不重合的子数据集，然后我们做K次模型训练和验证。每一次，我们使用一个子数据集验证模型，并使用其他K-1个子数据集来训练模型。在这K次训练和验证中，每次用来验证模型的子数据集都不同。最后，我们对这K次训练误差和验证误差分别求平均。过拟合和欠拟合接下来，我们将探究模型训练中经常出现的两类典型问题：
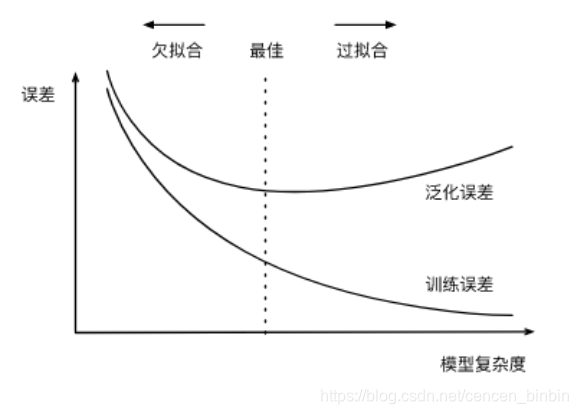
* 一类是模型无法得到较低的训练误差，我们将这一现象称作欠拟合（underfitting）；
* 另一类是模型的训练误差远小于它在测试数据集上的误差，我们称该现象为过拟合（overfitting）。 在实践中，我们要尽可能同时应对欠拟合和过拟合。虽然有很多因素可能导致这两种拟合问题，在这里我们重点讨论两个因素：模型复杂度和训练数据集大小。

给定训练数据集，模型复杂度和误差之间的关系：

训练数据集大小
影响欠拟合和过拟合的另一个重要因素是训练数据集的大小。一般来说，如果训练数据集中样本数过少，特别是比模型参数数量（按元素计）更少时，过拟合更容易发生。此外，泛化误差不会随训练数据集里样本数量增加而增大。因此，在计算资源允许的范围之内，我们通常希望训练数据集大一些，特别是在模型复杂度较高时，例如层数较多的深度学习模型。防止过拟合的方法：
（1）增加训练数据
（2）L2正则化

（3）丢弃法（dropout）

torch.cat(input1,,input2,1)  #按列合并并 
pow（input,exponent）#求张量input的exponent次值
torch.zeros_like(X)  #用于生成和输入tensor大小相同的全零tensor的。
model.train() #启用 BatchNormalization 和 Dropout
model.eval() #不启用 BatchNormalization 和 Dropout
pd.get_dummies(all_features, dummy_na=True)  #将离散数值改为特征

*2、梯度消失、梯度爆炸

随机初始化模型参数假设输出层只保留一个输出单元o1,且隐藏层使用相同的激活函数。如果将每个隐藏单元的参数都初始化为相等的值，那么在正向传播时每个隐藏单元将根据相同的输入计算出相同的值，并传递至输出层。在反向传播中，每个隐藏单元的参数梯度值相等。因此，这些参数在使用基于梯度的优化算法迭代后值依然相等。之后的迭代也是如此。在这种情况下，无论隐藏单元有多少，隐藏层本质上只有1个隐藏单元在发挥作用。因此，我们通常将神经网络的模型参数，特别是权重参数，进行随机初始化。

环境因素变化
1）协变量偏移
这里我们假设，虽然输入的分布可能随时间而改变，但是标记函数，即条件分布P（y∣x）不会改变。虽然这个问题容易理解，但在实践中也容易忽视。想想区分猫和狗的一个例子。我们的训练数据使用的是猫和狗的真实的照片，但是在测试时，我们被要求对猫和狗的卡通图片进行分类。统计学家称这种协变量变化是因为问题的根源在于特征分布的变化（即协变量的变化）。数学上，我们可以说P（x）改变了，但P（y∣x）保持不变。尽管它的有用性并不局限于此，当我们认为x导致y时，协变量移位通常是正确的假设。
2）标签偏移
当我们认为导致偏移的是标签P（y）上的边缘分布的变化，但类条件分布是不变的P（x∣y）时，就会出现相反的问题。当我们认为y导致x时，标签偏移是一个合理的假设。例如，通常我们希望根据其表现来预测诊断结果。在这种情况下，我们认为诊断引起的表现，即疾病引起的症状。有时标签偏移和协变量移位假设可以同时成立。例如，当真正的标签函数是确定的和不变的，那么协变量偏移将始终保持，包括如果标签偏移也保持。有趣的是，当我们期望标签偏移和协变量偏移保持时，使用来自标签偏移假设的方法通常是有利的。这是因为这些方法倾向于操作看起来像标签的对象，这（在深度学习中）与处理看起来像输入的对象（在深度学习中）相比相对容易一些。病因（要预测的诊断结果）导致 症状（观察到的结果）。训练数据集，数据很少只包含流感p(y)的样本。而测试数据集有流感p(y)和流感q(y)，其中不变的是流感症状p(x|y)。
3)概念偏移
另一个相关的问题出现在概念转换中，即标签本身的定义发生变化的情况。如果我们要建立一个机器翻译系统，分布P（y∣x）可能因我们的位置而异。这个问题很难发现。另一个可取之处是P（y∣x）通常只是逐渐变化。

**

**

3、 卷积神经网络

**
二维互相关运算
二维互相关（cross-correlation）运算的输入是一个二维输入数组和一个二维核（kernel）数组，输出也是一个二维数组，其中核数组通常称为卷积核或过滤器（filter）。卷积核的尺寸通常小于输入数组，卷积核在输入数组上滑动，在每个位置上，卷积核与该位置处的输入子数组按元素相乘并求和，得到输出数组中相应位置的元素。图1展示了一个互相关运算的例子，阴影部分分别是输入的第一个计算区域、核数组以及对应的输出。

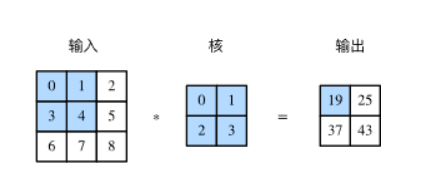
互相关运算与卷积运算
卷积层得名于卷积运算，但卷积层中用到的并非卷积运算而是互相关运算。我们将核数组上下翻转、左右翻转，再与输入数组做互相关运算，这一过程就是卷积运算。由于卷积层的核数组是可学习的，所以使用互相关运算与使用卷积运算并无本质区别。
特征图与感受野
二维卷积层输出的二维数组可以看作是输入在空间维度（宽和高）上某一级的表征，也叫特征图（feature map）。影响元素x 的前向计算的所有可能输入区域（可能大于输入的实际尺寸）叫做x的感受野。
填充
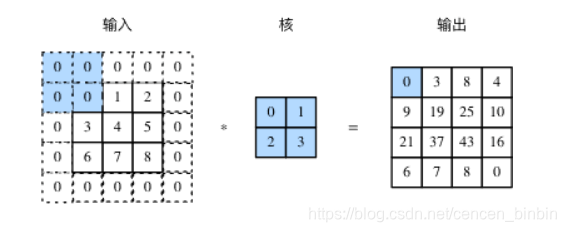
填充（padding）是指在输入高和宽的两侧填充元素（通常是0元素），图2里我们在原输入高和宽的两侧分别添加了值为0的元素。

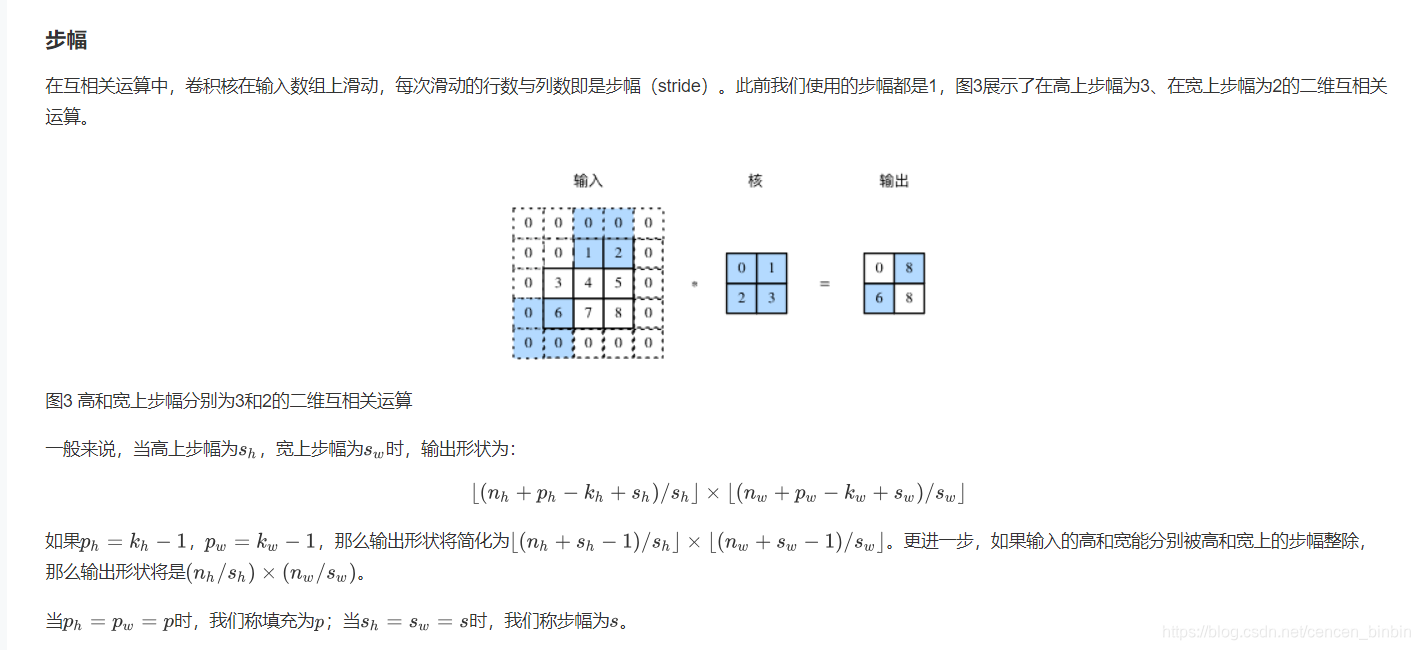
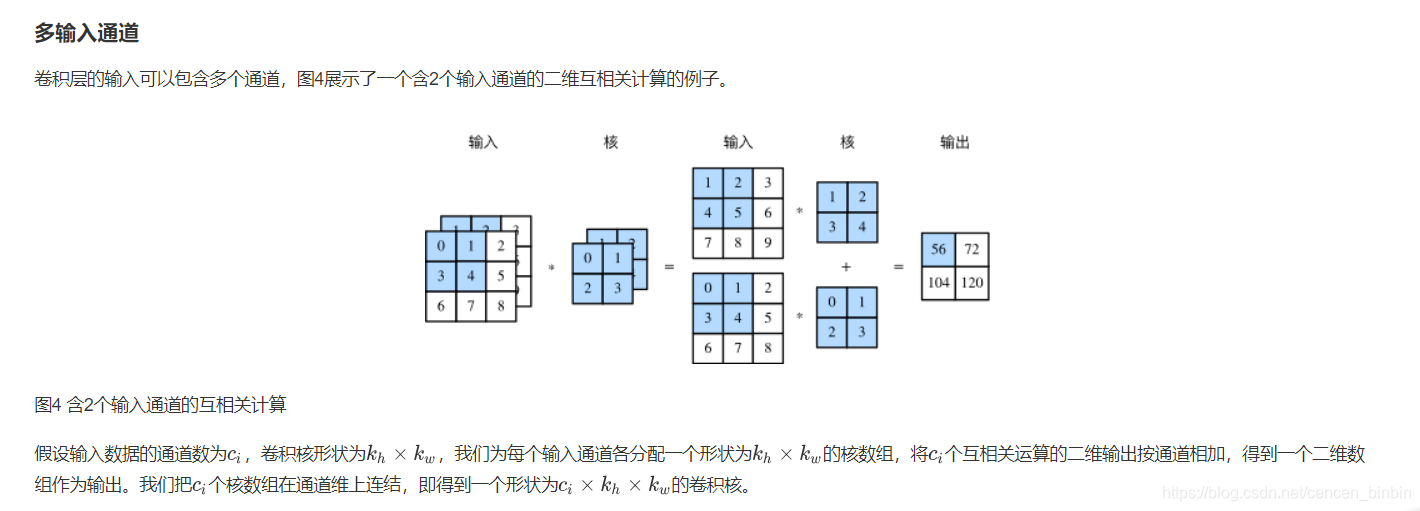
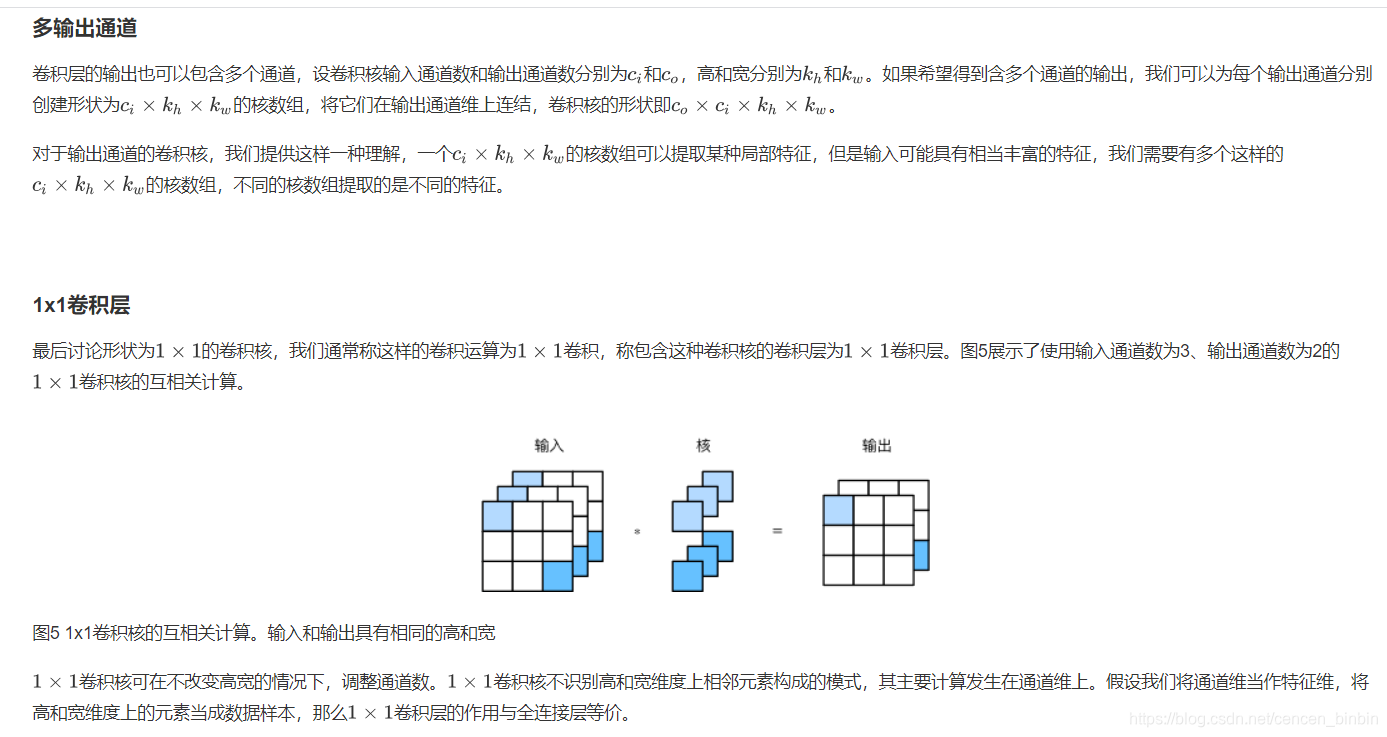
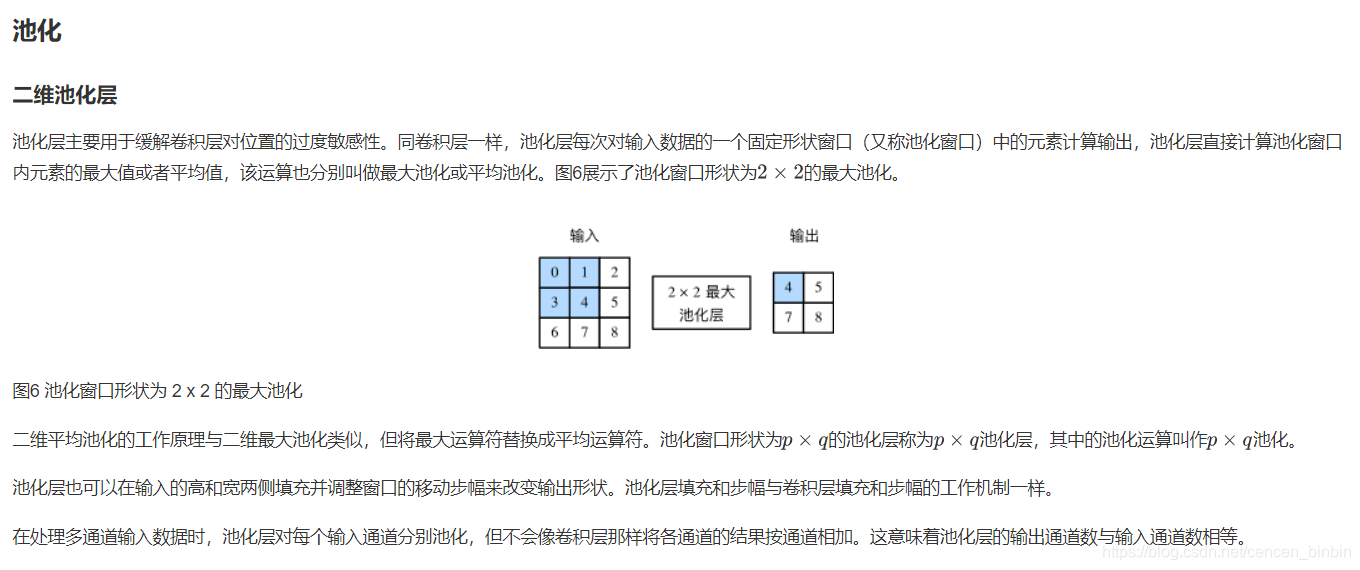
我们使用Pytorch中的nn.Conv2d类来实现二维卷积层，主要关注以下几个构造函数参数：

in_channels (python:int) – Number of channels in the input imag
out_channels (python:int) – Number of channels produced by the convolution
kernel_size (python:int or tuple) – Size of the convolving kernel
stride (python:int or tuple, optional) – Stride of the convolution. Default: 1
padding (python:int or tuple, optional) – Zero-padding added to both sides of the input. Default: 0
bias (bool, optional) – If True, adds a learnable bias to the output. Default: True