单链表中环的检测（JAVA）

单链表主类

参考单链表反转中的主类代码

检测思路

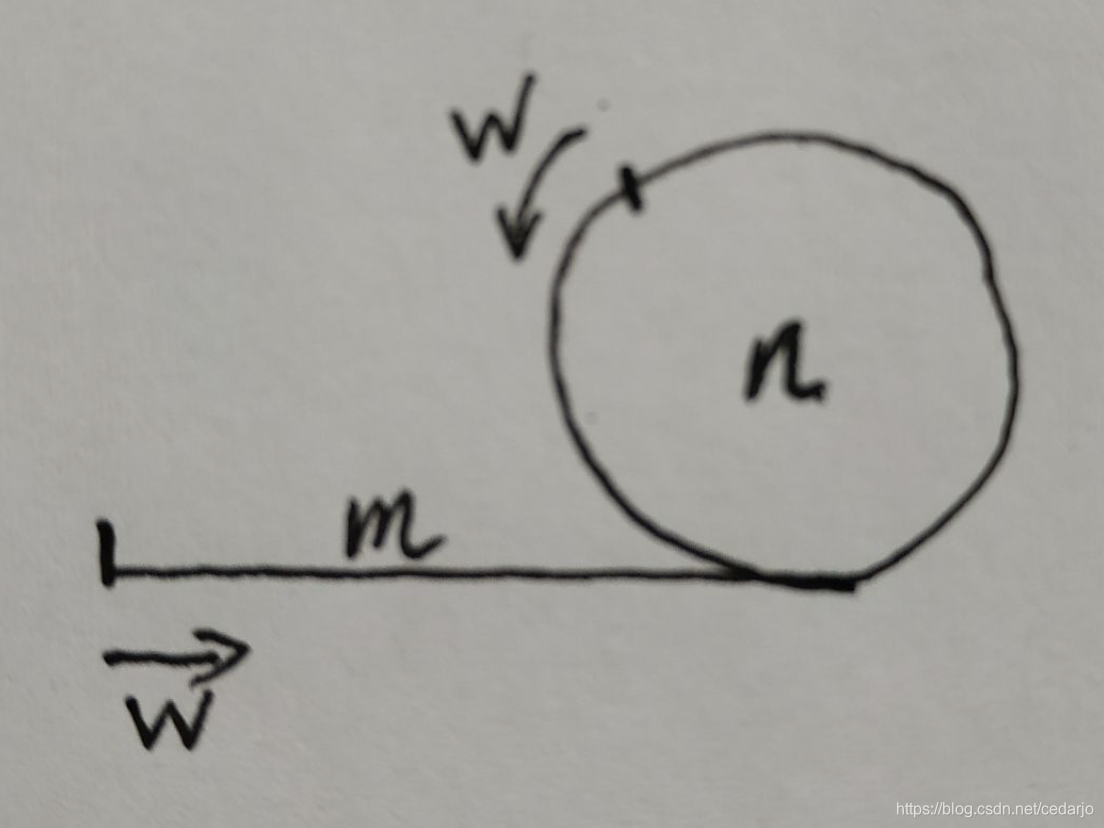
假设一个单链表是环形链表，那么该链表的元素总数可分为两部分
size = m + n
其中m是直线部分，n是环形部分
假想这是一个跑道，从直线跑道为起点，之后进入环形跑道，然后一直绕着环形跑道跑
现在有两个人一起从起点出发，速度不一致，快的速度为v，慢的速度为w，有v>w>0
假设两人足够有力量跑下去，那么这两人会不会在环形跑道的某点相遇呢？

经过时间t之后，如果满足如下公式，则两人可再次相遇
vt - wt = kn
其中k为整数
另一种说法就是：足够时间后，跑快的人是否一定可以超跑慢的人正好整数圈呢？
答案是肯定的，n就算再大，也经不起足够长的时间t，v-w就算再小，只要是个正数，就一定能在某个时间t后正好甩另一个人正好整数圈
单链表中环的检测就是利用了这个思想

代码

public boolean isCircle() {
	// 边界
    if (header == null) {
        return false;
    }
    // 相同的起跑线
    SinglyLinkedNode<T> faster = header, lower = header;
    // 如果跑快的人到达了终点，说明这条跑道没有环形部分
    while (faster != null && faster.getNext() != null) {
    	// 跑慢的人一次跑一步
        lower = lower.getNext();
        // 跑快的人一次跑两步
        faster = faster.getNext().getNext();
        // 如果两人相遇，表示有环形部分
        if (lower == faster) {
            return true;
        }
        // 两人未相遇则继续跑（根据前边的简单说明，有环形部分则一定会在某时某刻相遇，没有环形部分，则跑快的人肯定会先跑完，所以不会死循环）
    }
    return false;
}

环形入口定位思路

假定单链表确实存在环，接下来看怎么定位环的入口位置
在实现代码中可以看到，假定跑快的人速度为2，跑慢的人速度为1。
即v=2, w=1
带入上述公式vt - wt = kn得
t = kn
现在来看下跑快的人和跑慢的人各跑了多远
跑快的人：2kn
跑慢的人：kn
因为是在环上相遇，可计算出两人刚才各在环上跑了多远
跑快的人：2kn - m
跑慢的人：kn - m
现在暂时只考虑环上部分，他二人进入环形跑道的入口就是要定位的点，只要跑了整数圈就肯定还会回到改点。从二人已经在环上跑的路程来看，他们现在距离入口的距离相同，都是m，正好是直线跑道的距离。
而如果现在让刚才跑快的人休息，跑慢的人继续按原速度w=1跑，另外有一个人从直线的起点也按w=1开始跑，那么他二人一定会在环的入口相遇

代码

public SinglyLinkedNode<T> circleStartNode() {
	// 这里修改了isCircle方法的返回值为第一次相遇的节点位置
    SinglyLinkedNode<T> one = isCircle();
    if (one == null) {
        return null;
    }
    SinglyLinkedNode<T> another = header;
    while (one != another) {
        one = one.getNext();
        another = another.getNext();
    }
    return one;
}

环的长度思路

回到刚才快慢二人在环上相遇，因为二人的速度差是1，所以同一起点出发，不会出现某时刻快的人超过慢的人的问题
v=2, w=1
这是个追及问题，经过时间t后，快的人会正好超过慢的人一圈，即n
vt - wt = n带入求解t = n
所以t就等于环的长度值

代码

public int circleLength() {
    SinglyLinkedNode<T> start = isCircle();
    if (start == null) {
        return 0;
    }
    SinglyLinkedNode<T> faster = start, lower = start;
    int length = 0;
    while (length == 0 || faster != lower) {
        lower = lower.getNext();
        faster = faster.getNext().getNext();
        length++;
    }
    return length;
}

测试结果

a -> b -> c -> d -> e -> f -> g
index[0] : A;  index[1] : B;  index[2] : C;  index[3] : D;  index[4] : E;  index[5] : F;  index[6] : G;  
isCircle ? false
a -> b -> c -> d -> e -> f -> g -> a
index[0] : A;  index[1] : B;  index[2] : C;  index[3] : D;  index[4] : E;  index[5] : F;  index[6] : G;  index[7] : A;  index[8] : B;  index[9] : C;  
isCircle ? true
circle start node : A
circle length : 7
a -> b -> c -> d -> e -> f -> g -> b
index[0] : A;  index[1] : B;  index[2] : C;  index[3] : D;  index[4] : E;  index[5] : F;  index[6] : G;  index[7] : B;  index[8] : C;  index[9] : D;  
isCircle ? true
circle start node : B
circle length : 6
a -> b -> c -> d -> e -> f -> g -> c
index[0] : A;  index[1] : B;  index[2] : C;  index[3] : D;  index[4] : E;  index[5] : F;  index[6] : G;  index[7] : C;  index[8] : D;  index[9] : E;  
isCircle ? true
circle start node : C
circle length : 5
a -> b -> c -> d -> e -> f -> g - > d
index[0] : A;  index[1] : B;  index[2] : C;  index[3] : D;  index[4] : E;  index[5] : F;  index[6] : G;  index[7] : D;  index[8] : E;  index[9] : F;  
isCircle ? true
circle start node : D
circle length : 4
a -> b -> c -> d -> e -> f -> g -> e
index[0] : A;  index[1] : B;  index[2] : C;  index[3] : D;  index[4] : E;  index[5] : F;  index[6] : G;  index[7] : E;  index[8] : F;  index[9] : G;  
isCircle ? true
circle start node : E
circle length : 3
a -> b -> c -> d -> e -> f -> g -> f
index[0] : A;  index[1] : B;  index[2] : C;  index[3] : D;  index[4] : E;  index[5] : F;  index[6] : G;  index[7] : F;  index[8] : G;  index[9] : F;  
isCircle ? true
circle start node : F
circle length : 2
a -> b -> c -> d -> e -> f -> g -> g
index[0] : A;  index[1] : B;  index[2] : C;  index[3] : D;  index[4] : E;  index[5] : F;  index[6] : G;  index[7] : G;  index[8] : G;  index[9] : G;  
isCircle ? true
circle start node : G
circle length : 1