快速幂（矩阵快速幂）

最新推荐文章于 2025-05-03 13:20:41 发布

Only you, only you!

最新推荐文章于 2025-05-03 13:20:41 发布

阅读量418

点赞数

分类专栏：紫书算法学习记

本文链接：https://blog.youkuaiyun.com/ccnuacmhdu/article/details/76982640

版权

紫书算法学习记专栏收录该内容

64 篇文章

订阅专栏

一、快速幂【51nod1013】

求：3^0 + 3^1 +…+ 3^(N) mod 1000000007
Input
输入一个数N(0 <= N <= 10^9)
Output
输出：计算结果
Sample Input
3
Sample Output
40

【分析】
利用等比数列的求和公式得所求和是(3^{(n+1)-1)/2，如果暴力求3}(n+1)会超时，这里引入快速幂来加速。
思想类似这样，比如求3^{8，直接求的话就是8个3相乘，可以转换成4个9相乘，继续转换成2个81相乘，这样大大缩短了计算时间。而快速幂的思想，则是把幂当成二进制数，依次进行右移位运算，大大减少了运算次数，比如求3}10，此时幂是10=1010（2），规定幂模2等于1即幂&1等于1时，右移1位运算，并乘进结果，计算3^{10其实就是拆成了3}8和3^2这两个数相乘，快速幂代码具体实现结合本题如下示范：

【乘法逆元问题】
满足ak=1(mod p)的k值就是a关于p的乘法逆元。
(a/b)mod p=(ak)mod p

关于逆元的求法后续博客会补充，本题中的k=(1e9+7+1)/2

#include<iostream>

using namespace std;
const int mod=1e9+7;

long long mul(long long x,long long n)
{
    long long result=1,s=x;
    for(;n>0;n>>=1)
    {
        if(n&1)result=result*s%mod;
        s=s*s%mod;
    }
    return result;
}

int main()
{
    long long n;
    while(cin>>n)
    {
        cout<<((mul(3,n+1)-1%mod)%mod)*((mod+1)/2)%mod<<endl;
    }
    return 0;
}

二、矩阵快速幂Fibonacci POJ - 3070

In the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

An alternative formula for the Fibonacci sequence is

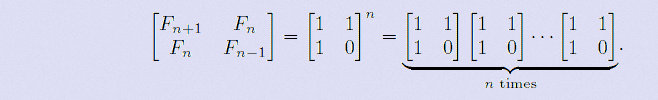
. 这里写图片描述

Given an integer n, your goal is to compute the last 4 digits of Fn.

Input
The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.

Output
For each test case, print the last four digits of Fn. If the last four digits of Fn are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print Fn mod 10000).

Sample Input
0
9
999999999
1000000000
-1
Sample Output
0
34
626
6875

AC代码：

矩阵快速幂和数的快速幂很类似，具体实现代码如下。【注意其中如果大数相乘可以使用俄罗斯农民乘法加速】

#include<iostream>
#include<cstring>

using namespace std;
const int mod=10000;
//俄罗斯农民乘法
long long pro(long long a,long long b)
{
    long long ret=0;
    for(;b>0;b>>=1)
    {
        if(b&1)ret=(ret+a)%mod;
        a=(a+a)%mod;
    }
    return ret;
}

class matrix
{
public:
    int n,m;
    int d[3][3];
    matrix(int a=0,int b=0)
    {
        n=a,m=b;
        memset(d,0,sizeof(d));
    }
    void _copy(int*t)
    {
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
                d[i][j]=*t++;
    }
    friend matrix operator * (const matrix &a,const matrix &b)
    {
        matrix c(a.n,b.m);
        for(int i=0;i<a.n;i++)
            for(int j=0;j<b.m;j++)
            {
                long long tmp=0;
                for(int k=0;k<a.m;k++)
                {
                    //tmp+=(long long)a.d[i][k]*b.d[k][j]%mod;
                    tmp+=pro((long long)a.d[i][k],(long long)b.d[k][j])%mod;
                    tmp%=mod;
                }
                c.d[i][j]=tmp;
            }
        return c;
    }
};

int solve(int n)
{
    if(n==0)return 0;
    matrix a,b;
    a.n=a.m=b.n=b.m=2;
    int aa[2*2]={
    1,1,
    1,0
    };
    int bb[2*2]={
    1,1,
    1,0
    };
    a._copy(aa);
    b._copy(bb);
    for(int i=n;i>0;i>>=1)
    {
        if(i&1)a=a*b;
        b=b*b;
    }
    return a.d[1][1];
}

int main()
{
    int n;
    while(cin>>n)
    {
        if(n==-1)break;
        cout<<solve(n)<<endl;
    }
    return 0;
}

三、矩阵快速幂Matrix Power Series POJ - 3233

Given a n × n matrix A and a positive integer k, find the sum S = A + A2 + A3 + … + Ak.

Input
The input contains exactly one test case. The first line of input contains three positive integers n (n ≤ 30), k (k ≤ 109) and m (m < 104). Then follow n lines each containing n nonnegative integers below 32,768, giving A’s elements in row-major order.

Output
Output the elements of S modulo m in the same way as A is given.

Sample Input
2 2 4
0 1
1 1
Sample Output
1 2
2 3

【提示】
本题如下直接求解为TLE
超时代码1：
for(int i=1;i<=k;i++)
{
result=add(mul(result,m),m);
}
超时代码2：
for(int i=1;i<=k;i++)
{
matrix tmp;
tmp=fast_pow(m,i);
result=add(tmp,result);
}
优化方法是利用递归的方式解决，列举其中两个和，比如(E是单位阵):
S(6)=A+A^2+…+A6=(A+A^2+A3)(E+A^3)=S(3)*(E+A3)
S(7)=A+A^2+…+A7=A+(A^2+A3+A^4)(E+A3)=A+S(3)(A+A^4)
通过观察这两个有代表性的前6、7项和，可以很快写出递归求解前k项和的函数，可以有效解决TLE

另外，注意本题用于运算的二维数组矩阵，如果定义成long long会TLE，要定义成int

AC代码：

#include<iostream>
#include<cstring>

using namespace std;
int mod;

typedef struct
{
    int n,m;
    int d[50][50];
}matrix;

matrix mul(matrix a,matrix b)
{
    matrix c;
    c.n=a.n,c.m=b.m;
    for(int i=0;i<a.n;i++)
        for(int j=0;j<b.m;j++)
        {
            int tmp=0;
            for(int k=0;k<a.m;k++)
            {
                tmp+=a.d[i][k]*b.d[k][j]%mod;
                tmp%=mod;
            }
            c.d[i][j]=tmp;
        }
    return c;
}

matrix fast_pow(matrix a,int n)
{
    matrix c;
    memset(c.d,0,sizeof(c.d));
    c.n=a.n,c.m=a.m;
    for(int i=0;i<a.n;i++)
        c.d[i][i]=1;
    for(;n>0;n>>=1)
    {
        if(n&1)c=mul(a,c);
        a=mul(a,a);
    }
    return c;
}

matrix add(matrix a,matrix b)
{
    matrix c;
    c.n=a.n,c.m=a.m;
    for(int i=0;i<a.n;i++)
        for(int j=0;j<a.m;j++)
        {
            c.d[i][j]=(a.d[i][j]+b.d[i][j])%mod;
        }
    return c;
}

matrix solve(matrix m,int k)//递归求解前k项和
{
    if(k==1)return m;
    matrix a=fast_pow(m,(k+1)/2);
    matrix b=solve(m,k/2);
    if(k&1)
    {
        return add(m,mul(b,add(m,a)));
    }
    else
    {
        return mul(b,add(a,fast_pow(a,0)));
    }
}

int main()
{
    int n,k;
    matrix m;
    matrix result;
    cin>>n>>k>>mod;
    m.m=m.n=n;
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
        {
            cin>>m.d[i][j];
        }
    result=solve(m,k);
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            cout<<result.d[i][j]<<" ";
        }
        cout<<endl;
    }
    return 0;
}