codeforces 552C Vanya and Scales_codeforces 552.c-优快云博客

本文链接：https://blog.youkuaiyun.com/cccccwb/article/details/86573116

题解：正解据说是进制转换……然鹅

实际上分析一下就会发现，可能参与配重的砝码的个数实际上只有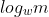 $log_{w}m$ 个，所以如果暴力计算的话，时间复杂度实际上是 $O(2^{log_{w}m})$ ，因为m虽然有1e9那么大，但是在w大于等于3的时候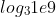， $log_{3}1e9$ 实际上也就只有19，是可以通过的，而w等于2的时候，答案一定是YES——因为任何一个数一定可以用二进制表示……

所以只要特判一下2的情况然后暴力枚举就可以通过这道题了。

代码如下：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string> 
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;

int cnt;
long long w,m;
long long ww[1010],s[1010];
int ansv;

void baoli(int n,long long nsum)
{
	if(nsum==m){ansv=1;return ;}
	if(n==0){if(abs(m-nsum)<=1) ansv=1;return ;}
	if(abs(m-nsum)>s[n]) return ;
	if(nsum<m)
	{
	  baoli(n-1,nsum+ww[n]);
	  if(ansv) return ;
	  baoli(n-1,nsum);
	}
	else
	{
	  baoli(n-1,nsum-ww[n]);
	  if(ansv) return ;
	  baoli(n-1,nsum);
	}
}

int main()
{
	cin>>w>>m;
	ww[0]=1;s[0]=1;
	while(ww[cnt]<m){cnt++;ww[cnt]=ww[cnt-1]*w;s[cnt]=s[cnt-1]+ww[cnt];}
	baoli(cnt,0);
	if(ansv) puts("YES");else puts("NO");
	return 0;
}