数据结构-树的基础部分

package com.chb.tree;

public class BinaryTreeDemo {
	public static void main(String[] args) {
		//需要创建一颗二叉树
		BinaryTree binaryTree=new BinaryTree();
		//创建需要的节点
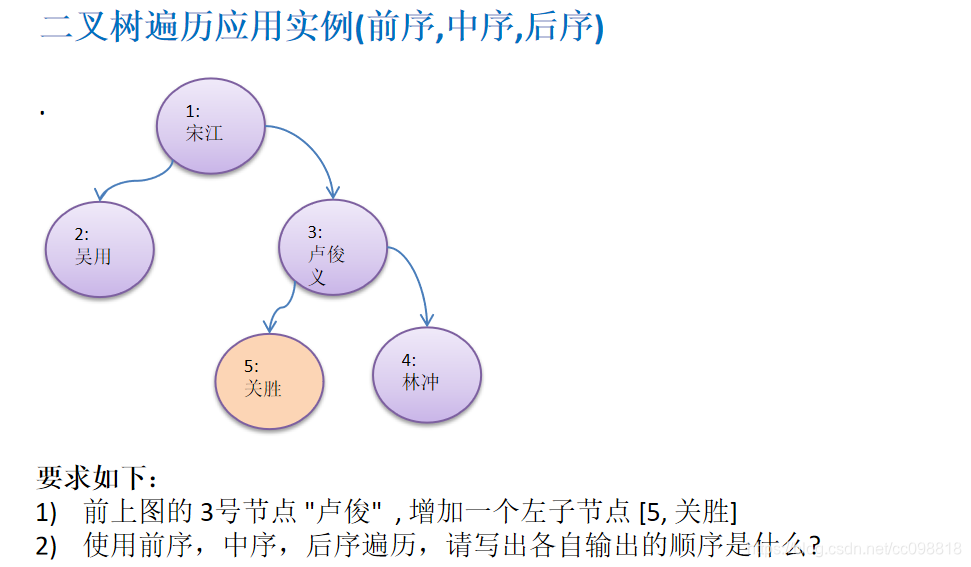
		HeroNode root = new HeroNode(1,"宋江");
		HeroNode node2=new HeroNode(2,"吴用");
		HeroNode node3=new HeroNode(3,"卢俊义");
		HeroNode node4=new HeroNode(4,"林冲");
		HeroNode node5 = new HeroNode(5,"关胜");
		//说明，我们先手动创建该二叉树，后面我们学习递归的方式创建二叉树
		root.setLeft(node2);
		root.setRight(node3);
		node3.setRight(node4);
		node3.setLeft(node5);
		binaryTree.setRoot(root);
		
		//测试
//		System.out.println("前序遍历"); // 1,2,3,5,4
//		binaryTree.preOrder();
		
//		System.out.println("中序遍历"); // 2,1,5,3,4
//		binaryTree.midOrder();
		
		System.out.println("后序遍历");  // 2,5,4,3,1
		binaryTree.endOrder();
	}
}

//定义BinaryTree二叉树
class BinaryTree {
	private HeroNode root;

	public void setRoot(HeroNode root) {
		this.root = root;
	}

	// 前序遍历
	public void preOrder() {
		if (this.root != null) {
			this.root.preOrder();
		} else {
			System.out.println("二叉树为空，无法遍历");
		}
	}

	// 中序遍历
	public void midOrder() {
		if (this.root != null) {
			this.root.midOrder();
		} else {
			System.out.println("二叉树为空，无法遍历");
		}
	}

	// 中序遍历
	public void endOrder() {
		if (this.root != null) {
			this.root.endOrder();
		} else {
			System.out.println("二叉树为空，无法遍历");
		}
	}
}

//先创建HeroNode节点
class HeroNode {
	private int no;
	private String name;
	private HeroNode left;
	private HeroNode right;

	public HeroNode(int no, String name) {
		super();
		this.no = no;
		this.name = name;
	}

	public int getNo() {
		return no;
	}

	public void setNo(int no) {
		this.no = no;
	}

	public String getName() {
		return name;
	}

	public void setName(String name) {
		this.name = name;
	}

	public HeroNode getLeft() {
		return left;
	}

	public void setLeft(HeroNode left) {
		this.left = left;
	}

	public HeroNode getRight() {
		return right;
	}

	public void setRight(HeroNode right) {
		this.right = right;
	}

	@Override
	public String toString() {
		return "HeroNode [no=" + no + ", name=" + name + "]";
	}

	// 前序遍历
	public void preOrder() {
		System.out.println(this);// 输出父节点
		// 递归向左子树前序遍历
		if (this.left != null) {
			this.left.preOrder();
		}
		// 递归向右子树前序遍历
		if (this.right != null) {
			this.right.preOrder();
		}
	}

	// 中序遍历
	public void midOrder() {
		// 递归向左子树前序遍历
		if (this.left != null) {
			this.left.midOrder();
		}
		System.out.println(this);// 输出父节点
		// 递归向右子树前序遍历
		if (this.right != null) {
			this.right.midOrder();
		}
	}

	// 后序遍历
	public void endOrder() {
		// 递归向左子树前序遍历
		if (this.left != null) {
			this.left.endOrder();
		}
		// 递归向右子树前序遍历
		if (this.right != null) {
			this.right.endOrder();
		}
		System.out.println(this);// 输出父节点
	}
}

运行结果：

package com.chb.tree;

public class BinaryTreeDemo {
	public static void main(String[] args) {
		// 需要创建一颗二叉树
		BinaryTree binaryTree = new BinaryTree();
		// 创建需要的节点
		HeroNode root = new HeroNode(1, "宋江");
		HeroNode node2 = new HeroNode(2, "吴用");
		HeroNode node3 = new HeroNode(3, "卢俊义");
		HeroNode node4 = new HeroNode(4, "林冲");
		HeroNode node5 = new HeroNode(5, "关胜");
		// 说明，我们先手动创建该二叉树，后面我们学习递归的方式创建二叉树
		root.setLeft(node2);
		root.setRight(node3);
		node3.setRight(node4);
		node3.setLeft(node5);
		binaryTree.setRoot(root);

		// 测试
//		System.out.println("前序遍历"); // 1,2,3,5,4
//		binaryTree.preOrder();

//		System.out.println("中序遍历"); // 2,1,5,3,4
//		binaryTree.midOrder();

//		System.out.println("后序遍历"); // 2,5,4,3,1
//		binaryTree.endOrder();

		// 前序遍历
		// 前序遍历的次数 ：4
//		System.out.println("前序遍历方式~~~");
//		HeroNode resNode = binaryTree.preOrderSearch(5);
//		if (resNode != null) {
//			System.out.printf("找到了，信息为 no=%d name=%s", resNode.getNo(), resNode.getName());
//		} else {
//			System.out.printf("没有找到 no = %d 的英雄", 5);
//		}

		// 中序遍历查找
		// 中序遍历3次
//		System.out.println("中序遍历方式~~~");
//		HeroNode resNode = binaryTree.infixOrderSearch(5);
//		if (resNode != null) {
//			System.out.printf("找到了，信息为 no=%d name=%s", resNode.getNo(), resNode.getName());
//		} else {
//			System.out.printf("没有找到 no = %d 的英雄", 5);
//		}
		
		// 后序遍历查找
		// 后序遍历查找的次数 2次
		System.out.println("后序遍历方式~~~");
		HeroNode resNode = binaryTree.postOrderSearch(5);
		if (resNode != null) {
			System.out.printf("找到了，信息为 no=%d name=%s", resNode.getNo(), resNode.getName());
		} else {
			System.out.printf("没有找到 no = %d 的英雄", 5);
		}
	}
}

//定义BinaryTree二叉树
class BinaryTree {
	private HeroNode root;

	public void setRoot(HeroNode root) {
		this.root = root;
	}

	// 前序遍历
	public void preOrder() {
		if (this.root != null) {
			this.root.preOrder();
		} else {
			System.out.println("二叉树为空，无法遍历");
		}
	}

	// 中序遍历
	public void midOrder() {
		if (this.root != null) {
			this.root.midOrder();
		} else {
			System.out.println("二叉树为空，无法遍历");
		}
	}

	// 中序遍历
	public void endOrder() {
		if (this.root != null) {
			this.root.endOrder();
		} else {
			System.out.println("二叉树为空，无法遍历");
		}
	}

	// 前序遍历
	public HeroNode preOrderSearch(int no) {
		if (root != null) {
			return root.preOrderSearch(no);
		} else {
			return null;
		}
	}

	// 中序遍历
	public HeroNode infixOrderSearch(int no) {
		if (root != null) {
			return root.infixOrderSearch(no);
		} else {
			return null;
		}
	}

	// 后序遍历
	public HeroNode postOrderSearch(int no) {
		if (root != null) {
			return this.root.postOrderSearch(no);
		} else {
			return null;
		}
	}
}

//先创建HeroNode节点
class HeroNode {
	private int no;
	private String name;
	private HeroNode left;
	private HeroNode right;

	public HeroNode(int no, String name) {
		super();
		this.no = no;
		this.name = name;
	}

	public int getNo() {
		return no;
	}

	public void setNo(int no) {
		this.no = no;
	}

	public String getName() {
		return name;
	}

	public void setName(String name) {
		this.name = name;
	}

	public HeroNode getLeft() {
		return left;
	}

	public void setLeft(HeroNode left) {
		this.left = left;
	}

	public HeroNode getRight() {
		return right;
	}

	public void setRight(HeroNode right) {
		this.right = right;
	}

	@Override
	public String toString() {
		return "HeroNode [no=" + no + ", name=" + name + "]";
	}

	// 前序遍历
	public void preOrder() {
		System.out.println(this);// 输出父节点
		// 递归向左子树前序遍历
		if (this.left != null) {
			this.left.preOrder();
		}
		// 递归向右子树前序遍历
		if (this.right != null) {
			this.right.preOrder();
		}
	}

	// 中序遍历
	public void midOrder() {
		// 递归向左子树前序遍历
		if (this.left != null) {
			this.left.midOrder();
		}
		System.out.println(this);// 输出父节点
		// 递归向右子树前序遍历
		if (this.right != null) {
			this.right.midOrder();
		}
	}

	// 后序遍历
	public void endOrder() {
		// 递归向左子树前序遍历
		if (this.left != null) {
			this.left.endOrder();
		}
		// 递归向右子树前序遍历
		if (this.right != null) {
			this.right.endOrder();
		}
		System.out.println(this);// 输出父节点
	}

	// 前序遍历查找
	/**
	 * 
	 * @param no 查找no
	 * @return 如果找到就返回该Node ,如果没有找到返回 null
	 */
	public HeroNode preOrderSearch(int no) {
		System.out.println("进入前序遍历");
		// 比较当前结点是不是
		if (this.no == no) {
			return this;
		}
		// 1.则判断当前结点的左子节点是否为空，如果不为空，则递归前序查找
		// 2.如果左递归前序查找，找到结点，则返回
		HeroNode resNode = null;
		if (this.left != null) {
			resNode = this.left.preOrderSearch(no);
		}
		if (resNode != null) {// 说明我们左子树找到
			return resNode;
		}
		// 1.左递归前序查找，找到结点，则返回，否继续判断，
		// 2.当前的结点的右子节点是否为空，如果不空，则继续向右递归前序查找
		if (this.right != null) {
			resNode = this.right.preOrderSearch(no);
		}
		return resNode;
	}

	// 中序遍历查找
	public HeroNode infixOrderSearch(int no) {
		// 判断当前结点的左子节点是否为空，如果不为空，则递归中序查找
		HeroNode resNode = null;
		if (this.left != null) {
			resNode = this.left.infixOrderSearch(no);
		}
		if (resNode != null) {
			return resNode;
		}
		System.out.println("进入中序查找");
		// 如果找到，则返回，如果没有找到，就和当前结点比较，如果是则返回当前结点
		if (this.no == no) {
			return this;
		}
		// 否则继续进行右递归的中序查找
		if (this.right != null) {
			resNode = this.right.infixOrderSearch(no);
		}
		return resNode;

	}

	// 后序遍历查找
	public HeroNode postOrderSearch(int no) {

		// 判断当前结点的左子节点是否为空，如果不为空，则递归后序查找
		HeroNode resNode = null;
		if (this.left != null) {
			resNode = this.left.postOrderSearch(no);
		}
		if (resNode != null) {// 说明在左子树找到
			return resNode;
		}

		// 如果左子树没有找到，则向右子树递归进行后序遍历查找
		if (this.right != null) {
			resNode = this.right.postOrderSearch(no);
		}
		if (resNode != null) {
			return resNode;
		}
		System.out.println("进入后序查找");
		// 如果左右子树都没有找到，就比较当前结点是不是
		if (this.no == no) {
			return this;
		}
		return resNode;
	}

}

运行结果：

package com.chb.tree;

public class BinaryTreeDemo {
	public static void main(String[] args) {
		// 需要创建一颗二叉树
		BinaryTree binaryTree = new BinaryTree();
		// 创建需要的节点
		HeroNode root = new HeroNode(1, "宋江");
		HeroNode node2 = new HeroNode(2, "吴用");
		HeroNode node3 = new HeroNode(3, "卢俊义");
		HeroNode node4 = new HeroNode(4, "林冲");
		HeroNode node5 = new HeroNode(5, "关胜");
		// 说明，我们先手动创建该二叉树，后面我们学习递归的方式创建二叉树
		root.setLeft(node2);
		root.setRight(node3);
		node3.setRight(node4);
		node3.setLeft(node5);
		binaryTree.setRoot(root);

		// 测试
//		System.out.println("前序遍历"); // 1,2,3,5,4
//		binaryTree.preOrder();

//		System.out.println("中序遍历"); // 2,1,5,3,4
//		binaryTree.midOrder();

//		System.out.println("后序遍历"); // 2,5,4,3,1
//		binaryTree.endOrder();

		// 前序遍历
		// 前序遍历的次数 ：4
//		System.out.println("前序遍历方式~~~");
//		HeroNode resNode = binaryTree.preOrderSearch(5);
//		if (resNode != null) {
//			System.out.printf("找到了，信息为 no=%d name=%s", resNode.getNo(), resNode.getName());
//		} else {
//			System.out.printf("没有找到 no = %d 的英雄", 5);
//		}

		// 中序遍历查找
		// 中序遍历3次
//		System.out.println("中序遍历方式~~~");
//		HeroNode resNode = binaryTree.infixOrderSearch(5);
//		if (resNode != null) {
//			System.out.printf("找到了，信息为 no=%d name=%s", resNode.getNo(), resNode.getName());
//		} else {
//			System.out.printf("没有找到 no = %d 的英雄", 5);
//		}

		// 后序遍历查找
		// 后序遍历查找的次数 2次
//		System.out.println("后序遍历方式~~~");
//		HeroNode resNode = binaryTree.postOrderSearch(5);
//		if (resNode != null) {
//			System.out.printf("找到了，信息为 no=%d name=%s", resNode.getNo(), resNode.getName());
//		} else {
//			System.out.printf("没有找到 no = %d 的英雄", 5);
//		}

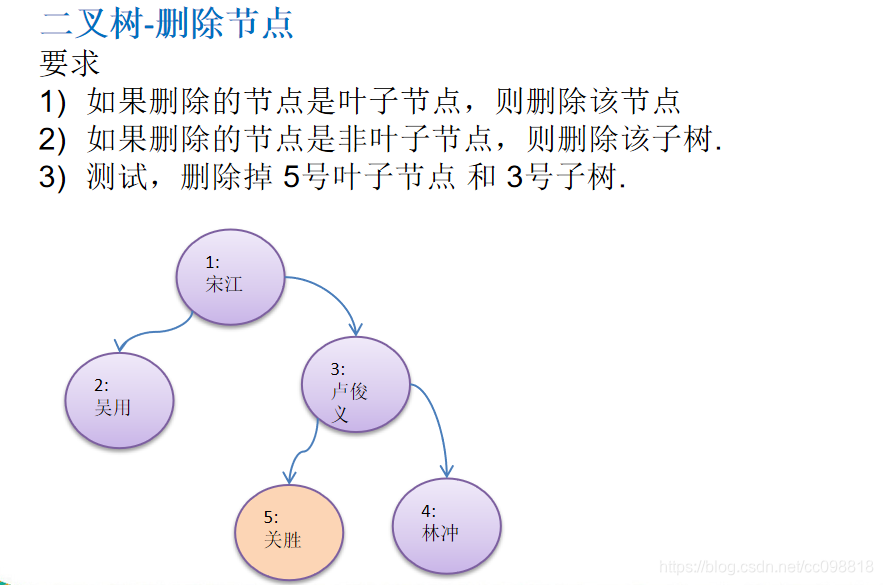
		// 测试一把删除结点

		System.out.println("删除前,前序遍历");
		binaryTree.preOrder(); // 1,2,3,5,4
		binaryTree.delNode(5);
		// binaryTree.delNode(3);
		System.out.println("删除后，前序遍历");
		binaryTree.preOrder(); // 1,2,3,4
	}
}

//定义BinaryTree二叉树
class BinaryTree {
	private HeroNode root;

	public void setRoot(HeroNode root) {
		this.root = root;
	}

	// 删除结点
	public void delNode(int no) {
		if (root != null) {
			// 如果只有一个root结点, 这里立即判断root是不是就是要删除结点
			if (root.getNo() == no) {
				root = null;
			} else {
				// 递归删除
				root.delNode(no);
			}
		} else {
			System.out.println("空树，不能删除~");
		}
	}

	// 前序遍历
	public void preOrder() {
		if (this.root != null) {
			this.root.preOrder();
		} else {
			System.out.println("二叉树为空，无法遍历");
		}
	}

	// 中序遍历
	public void midOrder() {
		if (this.root != null) {
			this.root.midOrder();
		} else {
			System.out.println("二叉树为空，无法遍历");
		}
	}

	// 中序遍历
	public void endOrder() {
		if (this.root != null) {
			this.root.endOrder();
		} else {
			System.out.println("二叉树为空，无法遍历");
		}
	}

	// 前序遍历
	public HeroNode preOrderSearch(int no) {
		if (root != null) {
			return root.preOrderSearch(no);
		} else {
			return null;
		}
	}

	// 中序遍历
	public HeroNode infixOrderSearch(int no) {
		if (root != null) {
			return root.infixOrderSearch(no);
		} else {
			return null;
		}
	}

	// 后序遍历
	public HeroNode postOrderSearch(int no) {
		if (root != null) {
			return this.root.postOrderSearch(no);
		} else {
			return null;
		}
	}
}

//先创建HeroNode节点
class HeroNode {
	private int no;
	private String name;
	private HeroNode left;
	private HeroNode right;

	public HeroNode(int no, String name) {
		super();
		this.no = no;
		this.name = name;
	}

	public int getNo() {
		return no;
	}

	public void setNo(int no) {
		this.no = no;
	}

	public String getName() {
		return name;
	}

	public void setName(String name) {
		this.name = name;
	}

	public HeroNode getLeft() {
		return left;
	}

	public void setLeft(HeroNode left) {
		this.left = left;
	}

	public HeroNode getRight() {
		return right;
	}

	public void setRight(HeroNode right) {
		this.right = right;
	}

	@Override
	public String toString() {
		return "HeroNode [no=" + no + ", name=" + name + "]";
	}

	// 前序遍历
	public void preOrder() {
		System.out.println(this);// 输出父节点
		// 递归向左子树前序遍历
		if (this.left != null) {
			this.left.preOrder();
		}
		// 递归向右子树前序遍历
		if (this.right != null) {
			this.right.preOrder();
		}
	}

	// 中序遍历
	public void midOrder() {
		// 递归向左子树前序遍历
		if (this.left != null) {
			this.left.midOrder();
		}
		System.out.println(this);// 输出父节点
		// 递归向右子树前序遍历
		if (this.right != null) {
			this.right.midOrder();
		}
	}

	// 后序遍历
	public void endOrder() {
		// 递归向左子树前序遍历
		if (this.left != null) {
			this.left.endOrder();
		}
		// 递归向右子树前序遍历
		if (this.right != null) {
			this.right.endOrder();
		}
		System.out.println(this);// 输出父节点
	}

	// 前序遍历查找
	/**
	 * 
	 * @param no 查找no
	 * @return 如果找到就返回该Node ,如果没有找到返回 null
	 */
	public HeroNode preOrderSearch(int no) {
		System.out.println("进入前序遍历");
		// 比较当前结点是不是
		if (this.no == no) {
			return this;
		}
		// 1.则判断当前结点的左子节点是否为空，如果不为空，则递归前序查找
		// 2.如果左递归前序查找，找到结点，则返回
		HeroNode resNode = null;
		if (this.left != null) {
			resNode = this.left.preOrderSearch(no);
		}
		if (resNode != null) {// 说明我们左子树找到
			return resNode;
		}
		// 1.左递归前序查找，找到结点，则返回，否继续判断，
		// 2.当前的结点的右子节点是否为空，如果不空，则继续向右递归前序查找
		if (this.right != null) {
			resNode = this.right.preOrderSearch(no);
		}
		return resNode;
	}

	// 中序遍历查找
	public HeroNode infixOrderSearch(int no) {
		// 判断当前结点的左子节点是否为空，如果不为空，则递归中序查找
		HeroNode resNode = null;
		if (this.left != null) {
			resNode = this.left.infixOrderSearch(no);
		}
		if (resNode != null) {
			return resNode;
		}
		System.out.println("进入中序查找");
		// 如果找到，则返回，如果没有找到，就和当前结点比较，如果是则返回当前结点
		if (this.no == no) {
			return this;
		}
		// 否则继续进行右递归的中序查找
		if (this.right != null) {
			resNode = this.right.infixOrderSearch(no);
		}
		return resNode;

	}

	// 后序遍历查找
	public HeroNode postOrderSearch(int no) {

		// 判断当前结点的左子节点是否为空，如果不为空，则递归后序查找
		HeroNode resNode = null;
		if (this.left != null) {
			resNode = this.left.postOrderSearch(no);
		}
		if (resNode != null) {// 说明在左子树找到
			return resNode;
		}

		// 如果左子树没有找到，则向右子树递归进行后序遍历查找
		if (this.right != null) {
			resNode = this.right.postOrderSearch(no);
		}
		if (resNode != null) {
			return resNode;
		}
		System.out.println("进入后序查找");
		// 如果左右子树都没有找到，就比较当前结点是不是
		if (this.no == no) {
			return this;
		}
		return resNode;
	}

	// 递归删除结点
	// 1.如果删除的节点是叶子节点，则删除该节点
	// 2.如果删除的节点是非叶子节点，则删除该子树
	public void delNode(int no) {
		// 思路
		/*
		 * 1. 因为我们的二叉树是单向的，所以我们是判断当前结点的子结点是否需要删除结点，而不能去判断当前这个结点是不是需要删除结点. 2.
		 * 如果当前结点的左子结点不为空，并且左子结点 就是要删除结点，就将this.left = null; 并且就返回(结束递归删除) 3.
		 * 如果当前结点的右子结点不为空，并且右子结点 就是要删除结点，就将this.right= null ;并且就返回(结束递归删除) 4.
		 * 如果第2和第3步没有删除结点，那么我们就需要向左子树进行递归删除 5. 如果第4步也没有删除结点，则应当向右子树进行递归删除.
		 * 
		 */
		// 2. 如果当前结点的左子结点不为空，并且左子结点 就是要删除结点，就将this.left = null; 并且就返回(结束递归删除)
		if (this.left != null && this.left.no == no) {
			this.left = null;
			return;
		}
		// 3.如果当前结点的右子结点不为空，并且右子结点 就是要删除结点，就将this.right= null ;并且就返回(结束递归删除)
		if (this.right != null && this.right.no == no) {
			this.right = null;
			return;
		}
		// 4.我们就需要向左子树进行递归删除
		if (this.left != null) {
			this.left.delNode(no);
		}
		// 5.则应当向右子树进行递归删除
		if (this.right != null) {
			this.right.delNode(no);
		}
	}
}

运行结果：

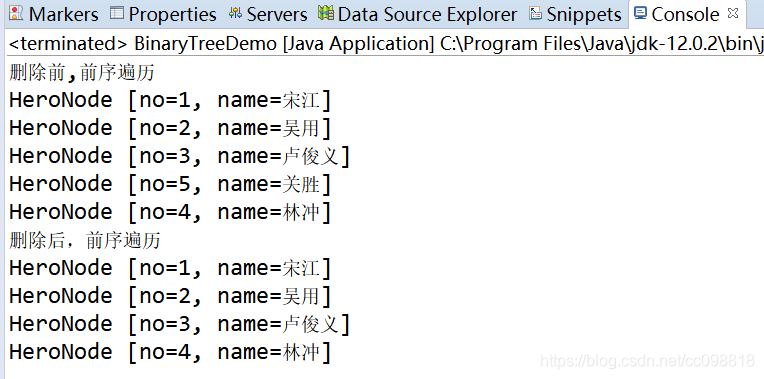
package com.chb.tree;

public class ArrBinaryTreeDemo {
	public static void main(String[] args) {
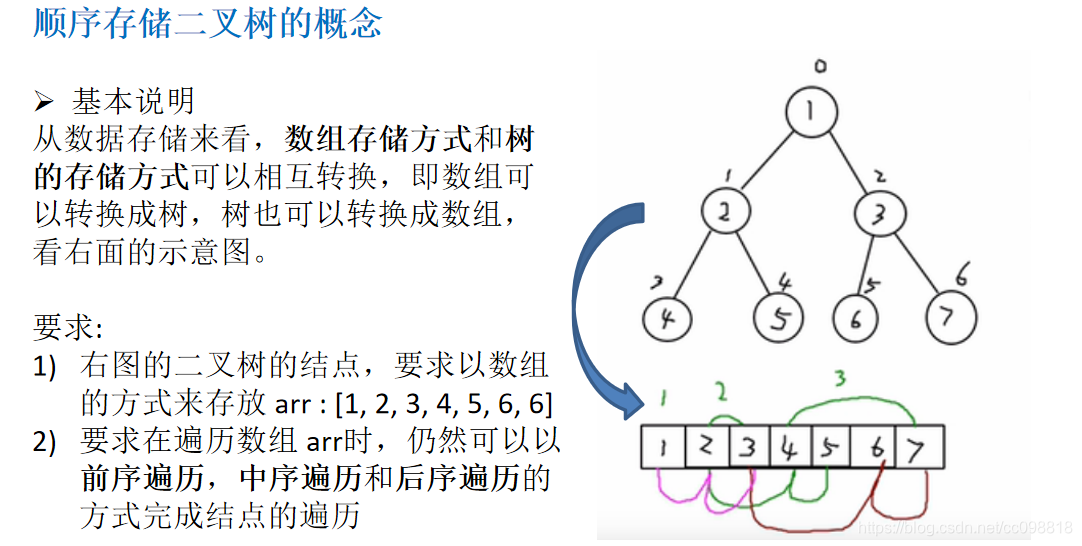
		int[] arr = { 1, 2, 3, 4, 5, 6, 7 };
		// 创建一个 ArrBinaryTree
		ArrBinaryTree arrBinaryTree = new ArrBinaryTree(arr);
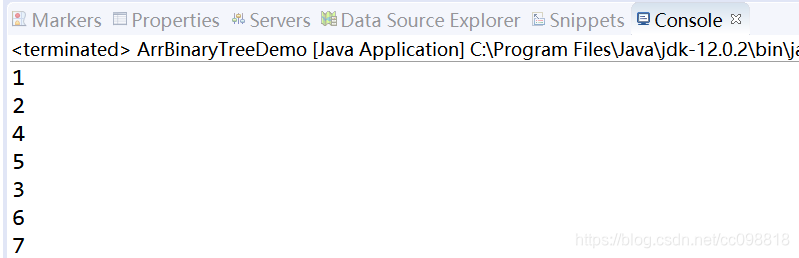
		arrBinaryTree.preOrder(0); // 1,2,4,5,3,6,7
	}
}

class ArrBinaryTree {
	private int[] arr;// 存储数据结点的数组

	public ArrBinaryTree(int[] arr) {
		super();
		this.arr = arr;
	}

	// 编写一个方法，完成顺序存储二叉树的前序遍历
	public void preOrder(int index) {// index 数组的下标
		// 如果数组为空，或者 arr.length = 0
		if (arr == null || arr.length == 0) {
			System.out.println("数组为空，不能按照二叉树的前序遍历");
		}
		// 输出当前这个元素
		System.out.println(arr[index]);
		// 向左递归遍历
		if ((index * 2 + 1) < arr.length) {
			preOrder(2 * index + 1);
		}
		// 向右递归遍历
		if ((index * 2 + 2) < arr.length) {
			preOrder(2 * index + 2);
		}
	}

}

运行结果：