毕设项目 常用的机器学习算法汇总

0 前言

Hi，这里是丹成学长。

不少同学的毕业设计是与机器学习算法相关的，很多同学这一块的基础比较薄弱，学长这里给大家分享一下毕设中常用的机器学习算法

毕设帮助，开题指导，资料分享，疑问解答(见文末)

🧿 选题指导, 项目分享：见文末

1 朴素贝叶斯算法及原理概述

1.1 朴素贝叶斯简介

• 朴素贝叶斯算法是基于贝叶斯定理和特征条件独立假设的一种分类方法

• 朴素贝叶斯算法是一种基于联合概率分布的统计学习方法

• 朴素贝叶斯算法实现简单,效果良好,是一种常用的机器学习方法

1.2 贝叶斯定理

朴素贝叶斯算法的一个基础是贝叶斯定理

贝叶斯定理（英语：Bayes’ theorem）是[概率论]中的一个[定理]，描述在已知一些条件下，某事件的发生概率。
比如，如果已知某癌症与寿命有关，使用贝叶斯定理则可以通过得知某人年龄，来更加准确地计算出他罹患癌症的概率。

通常，事件A在事件B已发生的条件下发生的概率，与事件B在事件A已发生的条件下发生的概率是不一样的。
然而，这两者是有确定的关系的，贝叶斯定理就是这种关系的陈述。
贝叶斯公式的一个用途，即通过已知的三个概率而推出第四个概率。贝叶斯定理跟[随机变量]的[条件概率]以及[边缘概率分布]有关。

作为一个普遍的原理，贝叶斯定理对于所有概率的解释是有效的。这一定理的主要应用为[贝叶斯推断]，是[推论统计学]中的一种推断法。这一定理名称来自于[托马斯·贝叶斯]。

1.3 算法原理

贝叶斯定理是关于随机事件A和B的条件概率的一则定理。

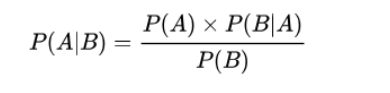
其中P(A|B)是指在事件B发生的情况下事件A发生的概率。

在贝叶斯定理中，每个名词都有约定俗成的名称：

• P(A|B)是已知B发生后A的条件概率，也由于得自B的取值而被称作A的后验概率。
• P(A)是A的先验概率（或边缘概率）。之所以称为"先验"是因为它不考虑任何B方面的因素。
• P(B|A)是已知A发生后B的条件概率，也由于得自A的取值而被称作B的后验概率。
• P(B)是B的先验概率或边缘概率。

按这些术语，贝叶斯定理可表述为：

后验概率 = (似然性*先验概率)/标准化常量
也就是说，后验概率与先验概率和相似度的乘积成正比。

另外，比例P(B|A)/P(B)也有时被称作标准似然度（standardised likelihood），贝叶斯定理可表述为：

后验概率 = 标准似然度*先验概率

1.4 朴素贝叶斯算法

• 朴素叶斯算法的基本假设是条件独立性,这是一一个较强的前提条件,因而朴素贝叶斯算法易于实现,但是分类性能可能不会很高

• 朴素贝叶斯算法要求输入变量是条件独立的,但是如果它们之间存在概率依存关系,就超出该算法范畴,属于贝叶斯网络

• 首先计算先验概率及条件概率

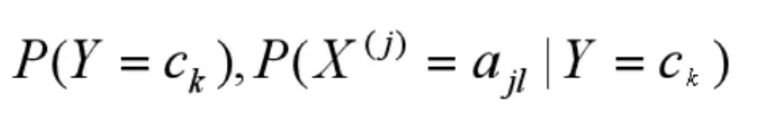
其中

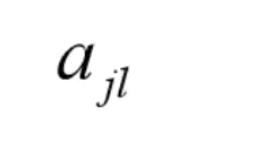
代表第j个特征可能取第I个值

◆ 对于每一个给定的特征向量X ,在不同类别中出现的概率为

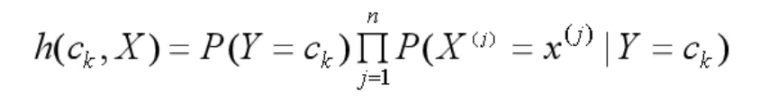
◆ 那么,最终预测结果y自然是其中概率最大的那个:

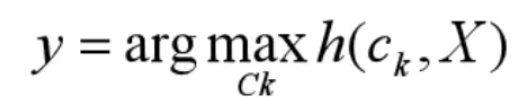
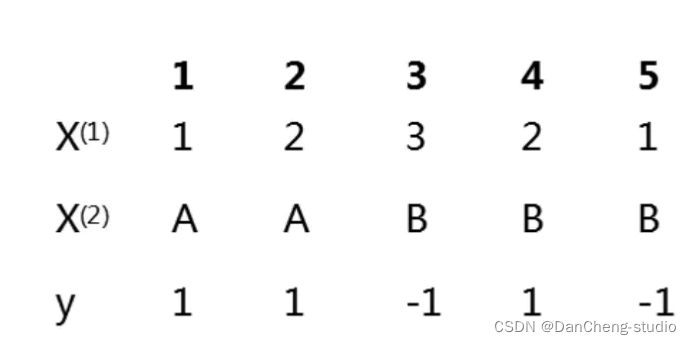
1.5 朴素贝叶斯算法示例

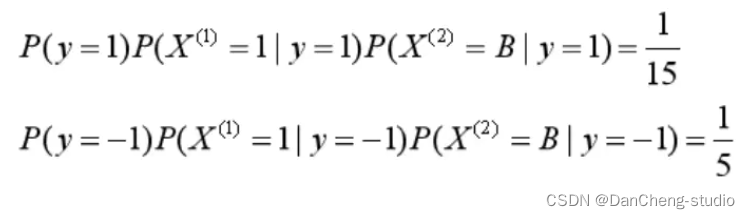
1.6 朴素贝叶斯分类使用

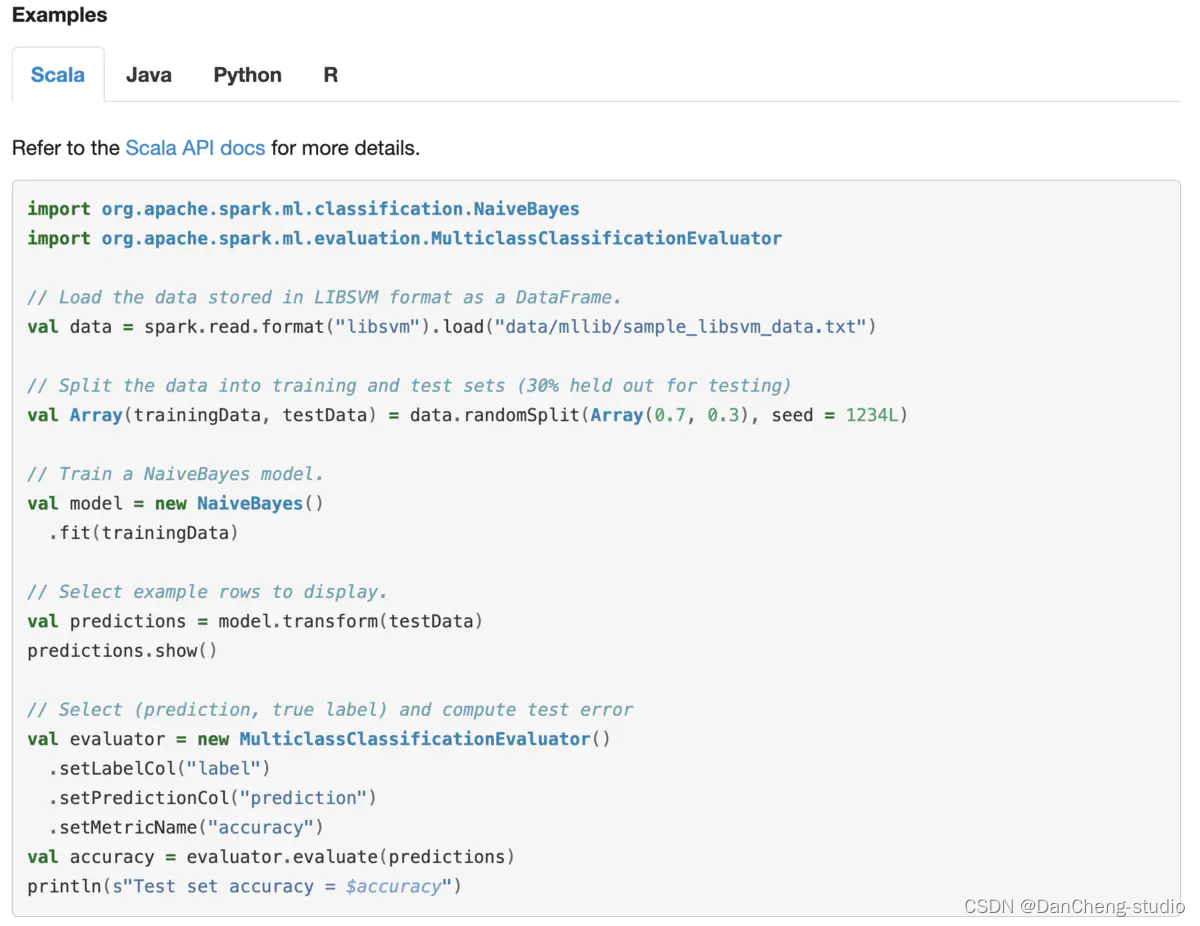
我们看看官方文档是怎么说的

翻译一下

朴素贝叶斯分类器是一类简单的概率多类分类器，它基于应用贝叶斯定理，在每对特征之间具有强（天真）独立假设。
朴素贝叶斯可以非常有效地训练。通过对训练数据的单次传递，它计算给定每个标签的每个特征的条件概率分布。
对于预测，它应用贝叶斯定理来计算给定观察的每个标签的条件概率分布。
MLlib支持多项式朴素贝叶斯和伯努利朴素贝叶斯。
输入数据：这些模型通常用于文档分类。在该上下文中，每个观察是一个文档，每个特征代表一个术语。特征值是术语的频率（在多项式朴素贝叶斯中）或零或一个，表示该术语是否在文档中找到（在伯努利朴素贝叶斯中）。要素值必须为非负值。使用可选参数“multinomial”或“bernoulli”选择模型类型，默认为“multinomial”。对于文档分类，输入特征向量通常应该是稀疏向量。由于训练数据仅使用一次，因此不必对其进行缓存。
通过设置参数λ（默认为1.0）可以使用加法平滑。

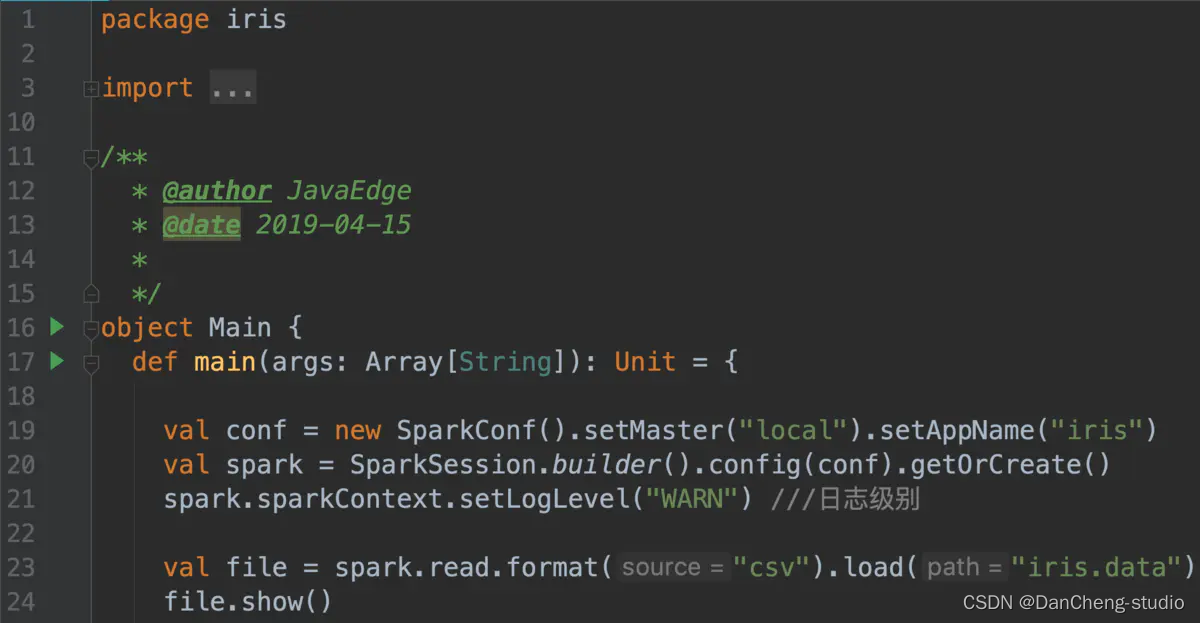
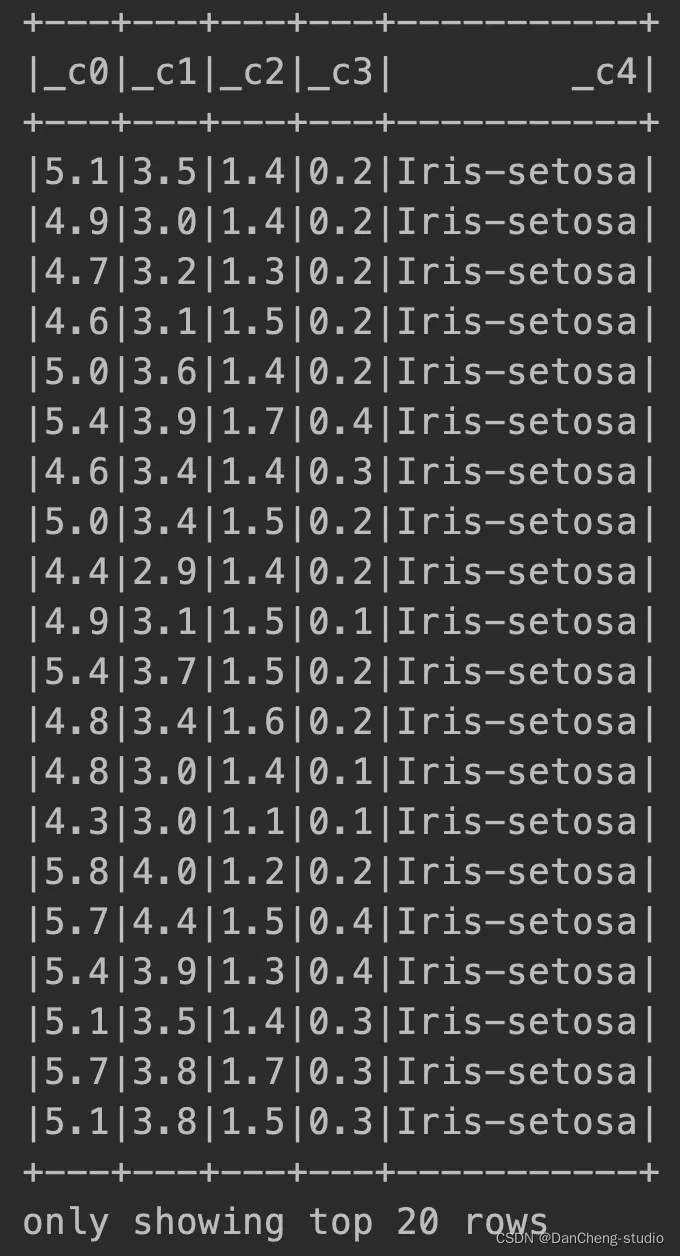
file.show

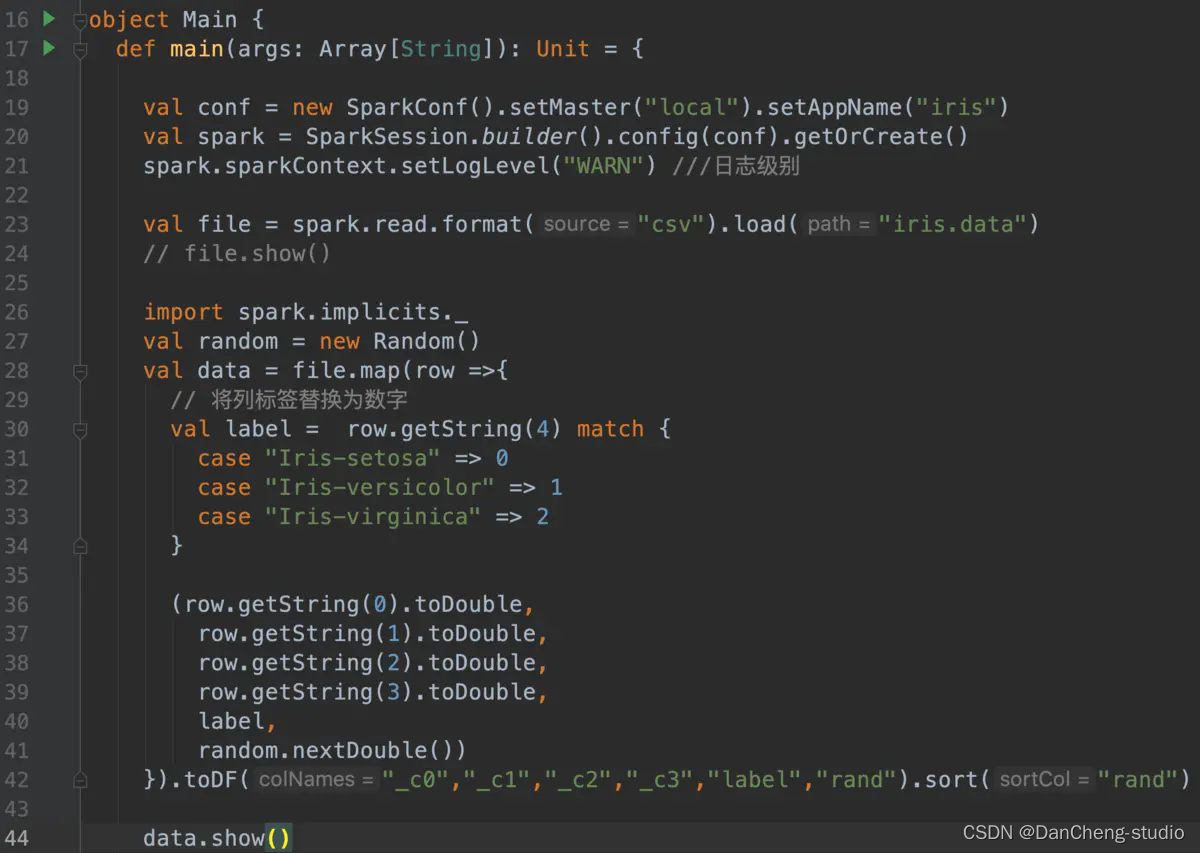
打乱顺序 - data.show

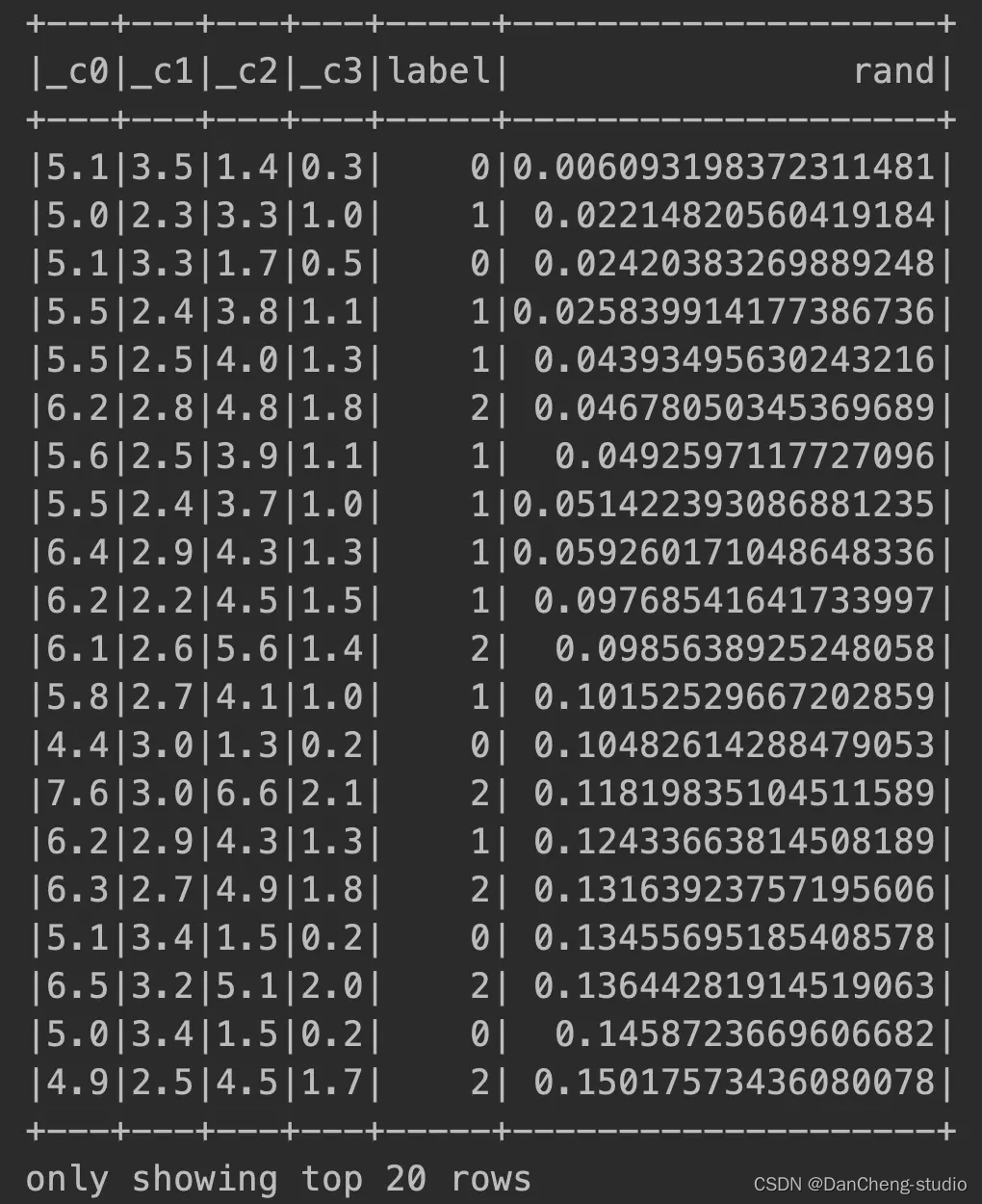
在特征标签形成vector数组

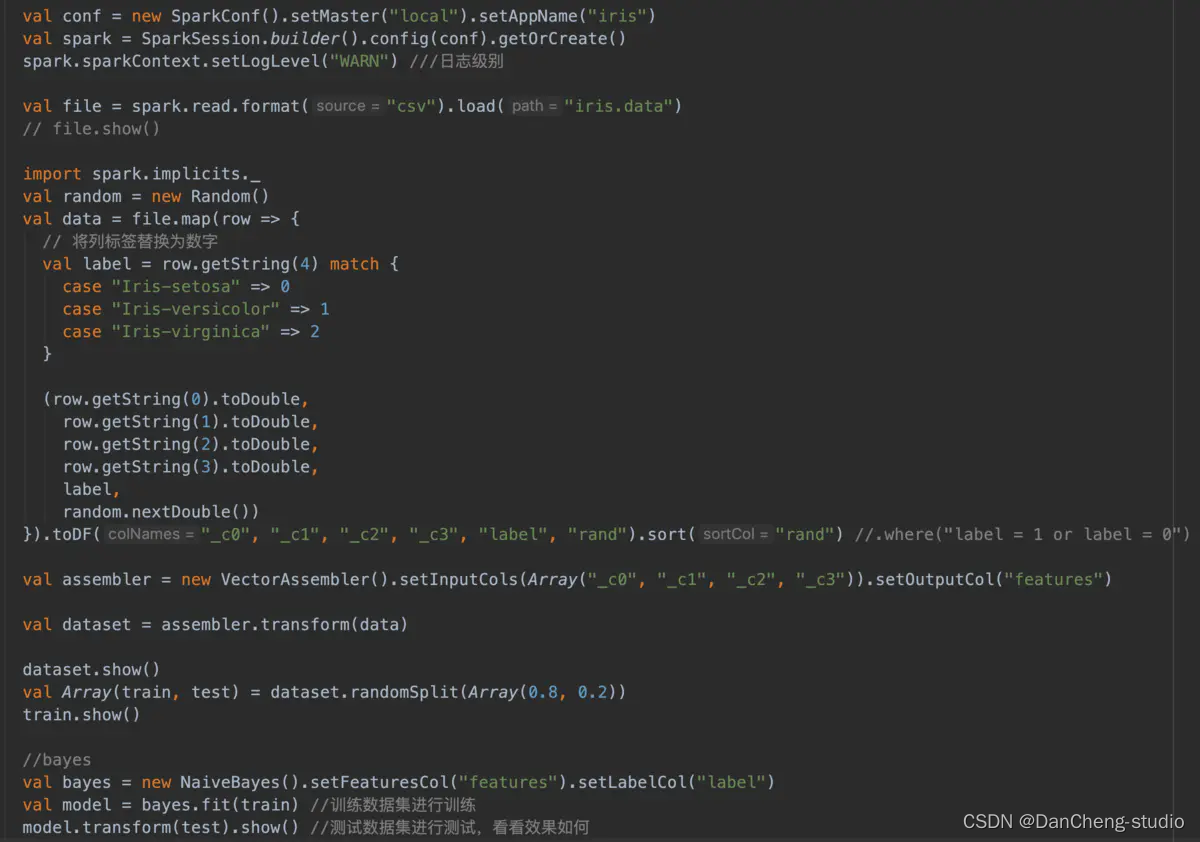
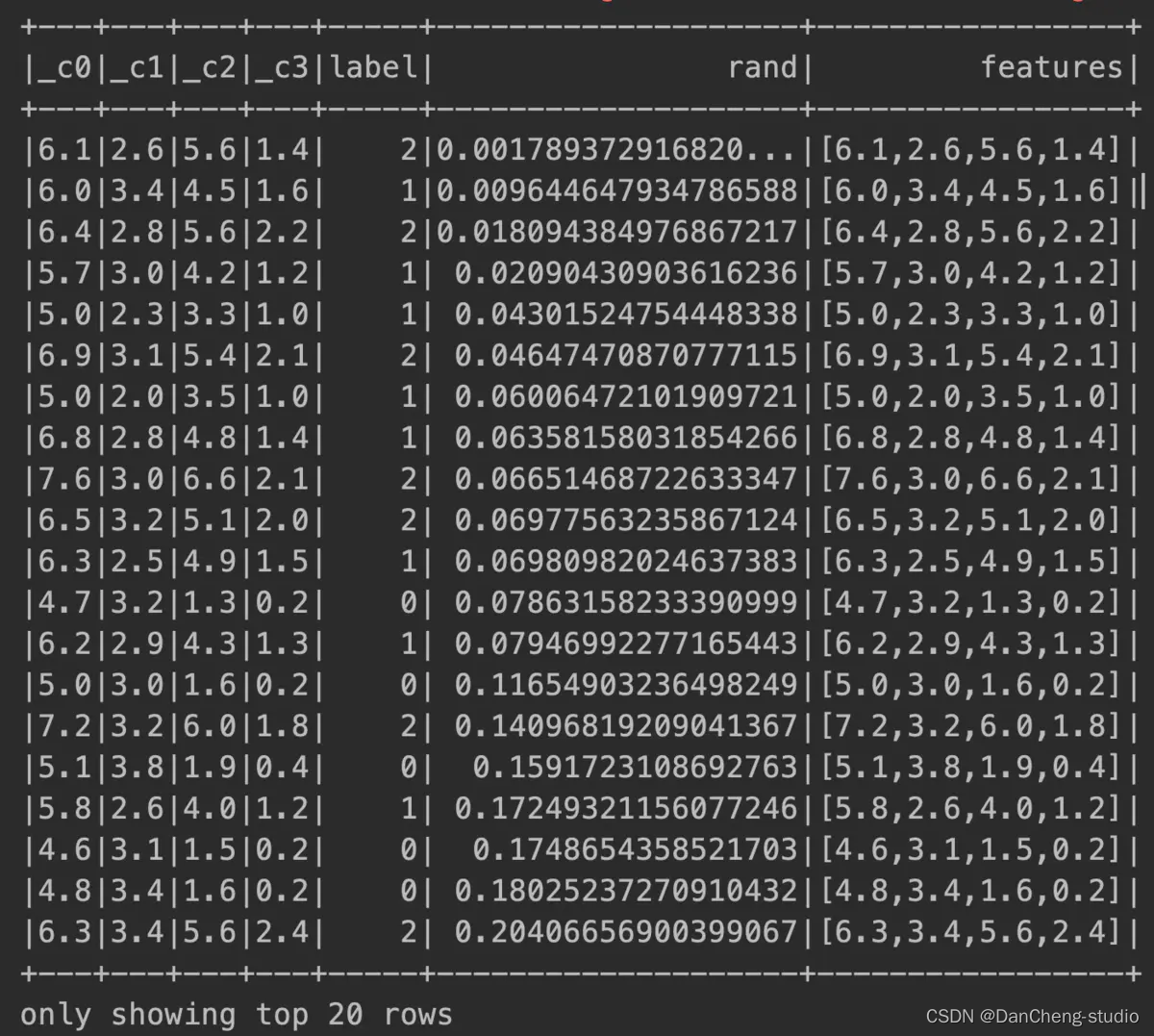
训练集预测

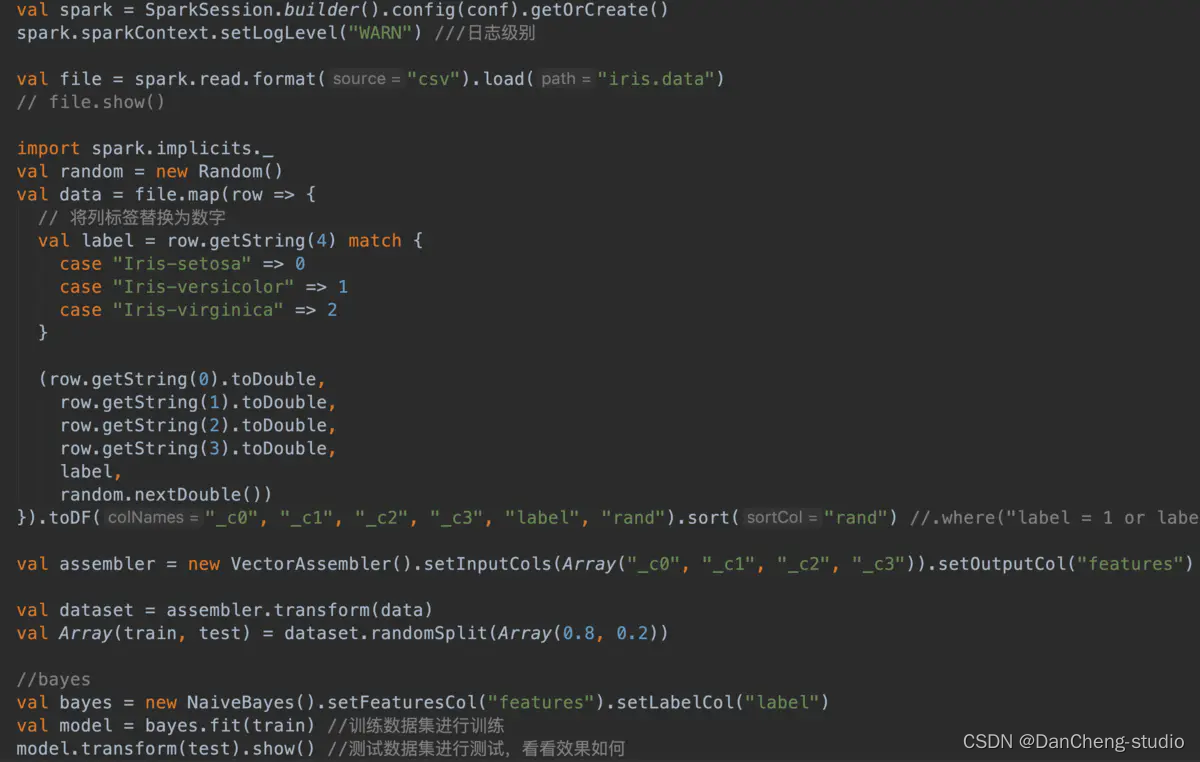
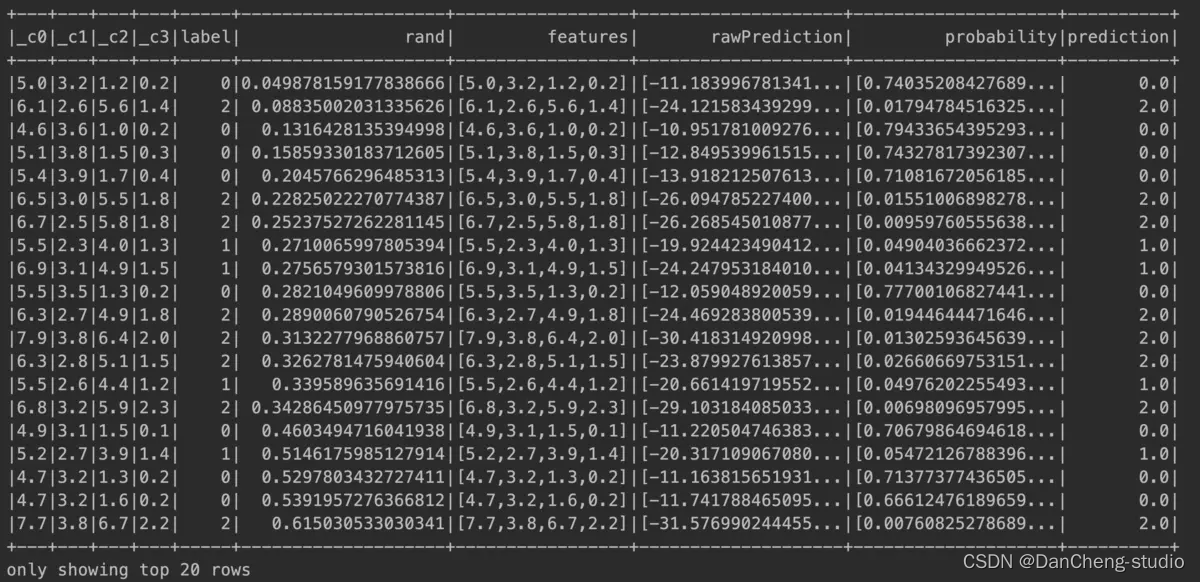
都是正确的,完美预测!

2 支持向量机算法

2.1 简介

• 支持向量机(SVM)是一种用来分类的算法,当然,在这基础上进行改进,也可以进行回归分析(SVR)

• SVM是最优秀的分类算法之一，即便是在如今深度学习盛行的时代,仍然具有很广泛的应用

• SVM被设计成一种二分类的算法， 当然,也有人提出了使用SVM进行多分类的方法,但是SVM依然主要被用在二分类中

在[机器学习]中，支持向量机（英语：support vector machine，常简称为SVM，又名支持向量网络）是在[分类]与[回归分析]中分析数据的监督式学习模型与相关的学习算法。

给定一组训练实例，每个训练实例被标记为属于两个类别中的一个或另一个，SVM训练算法创建一个将新的实例分配给两个类别之一的模型，使其成为非概率[二元][线性分类器]。

SVM模型是将实例表示为空间中的点，这样映射就使得单独类别的实例被尽可能宽的明显的间隔分开。然后，将新的实例映射到同一空间，并基于它们落在间隔的哪一侧来预测所属类别。

除了进行线性分类之外，SVM还可以使用所谓的[核技巧]有效地进行非线性分类，将其输入隐式映射到高维特征空间中。

当数据未被标记时，不能进行监督式学习，需要用[非监督式学习]，它会尝试找出数据到簇的自然聚类，并将新数据映射到这些已形成的簇。将支持向量机改进的聚类算法被称为支持向量聚类，当数据未被标记或者仅一些数据被标记时，支持向量聚类经常在工业应用中用作分类步骤的预处理。

2.2 简单的分类

• 可能大家认为最简单的一种分类方法大概就是划分"阈值"了

• 例如判断一一个人是否是秃头:头顶区域头发数量小于100根则是秃头

• 而SVM也是遵循这个道理,只不过它的"阈值”寻找过程更复杂,也更科学

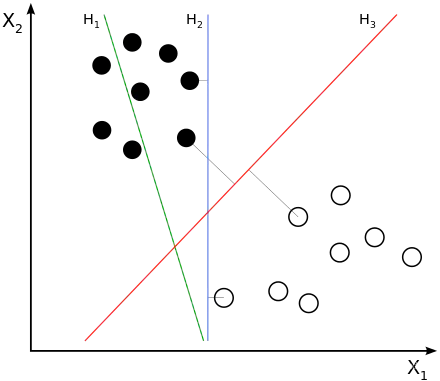
2.3 SVM的基本思想

• SVM的主要思想是寻找能够将数据进行分类的平面或超平面,在平面上的则是A类,在平面下的则是B类, 因此，SVM是一种二分类算法

• 因此，这个“阈值”更贴切地说应该称为“边界”, 而这个"边界"恰恰就是通过向量来表示的,故而这个"边界"我们就称为支持向量

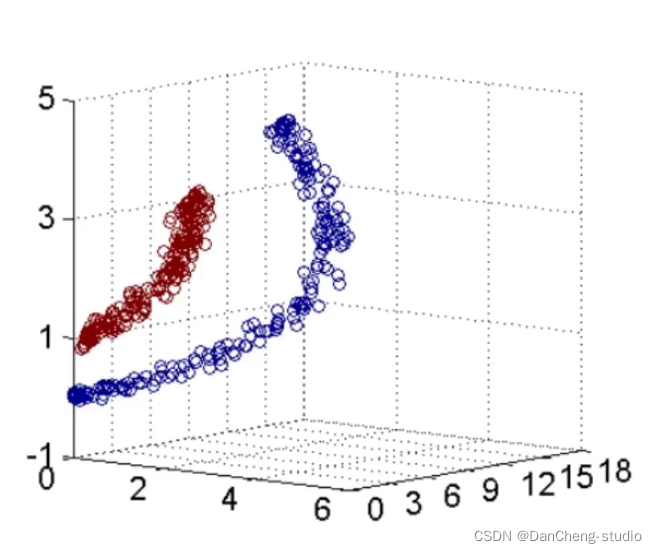
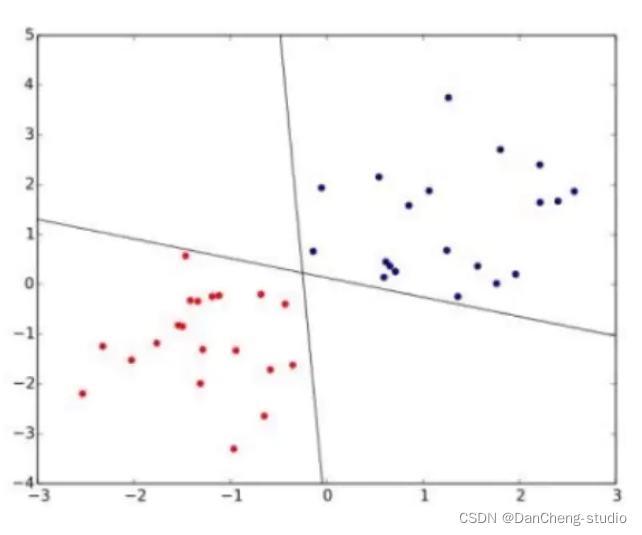
2.4 SVM处理非线性问题

• 在很多情况下,数据集并不是线性可分的,譬如:

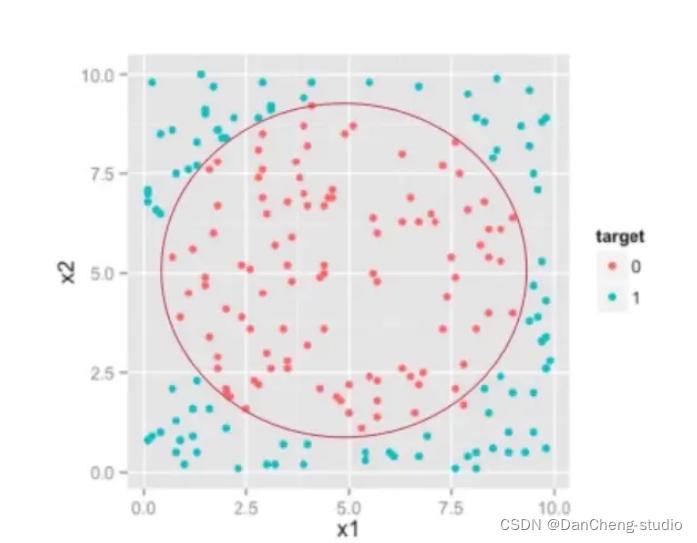
2.5 SVM的核函数

• SVM虽然只能进行线性分类, 但是,可以通过引入核函数,将非线性的数据,转化为另一个空间中的线性可分数据,这叫做支持向量机的核技巧,可以认为是支持向量机的精髓之一
  

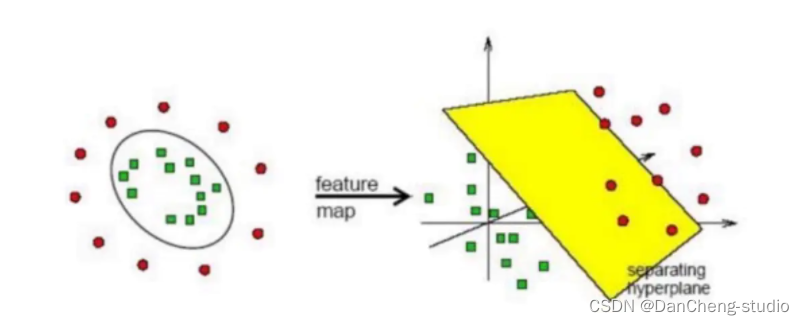
SVM的类别

• 基于硬间隔最大化的线性可分 支持向量机

• 基于软间隔最大化的线性支持向量机

• 使用核函数的非线性支持向量机

2.6 SVM分类实现

支持向量机在高维或无限维空间中构造超平面或超平面集，其可用于分类，回归或其他任务。 直观地，通过与任何类的最近的训练数据点具有最大距离的超平面（所谓的功能边界）实现良好的分离，因为通常边缘越大，分类器的泛化误差越低。
Spark ML中的LinearSVC支持使用线性SVM进行二进制分类。 在内部，它使用OWLQN优化器优化铰链损耗

代码

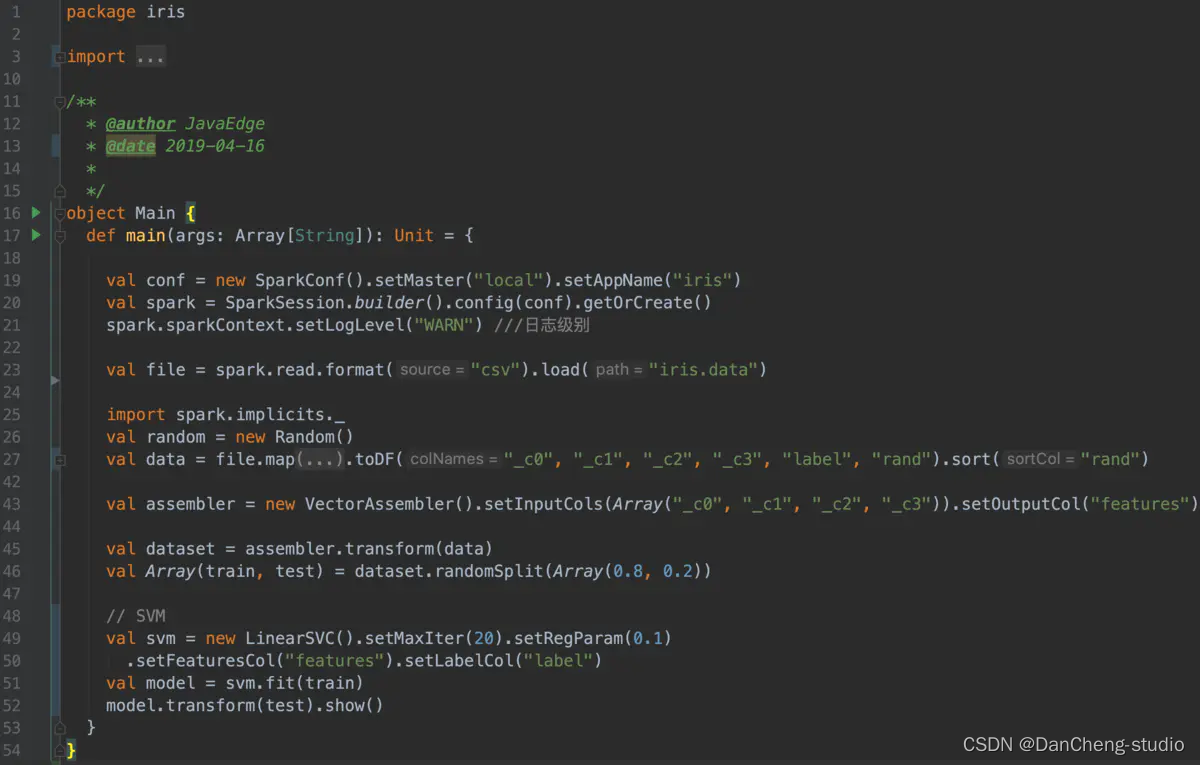
iris数据集特征三列,所以报错

只是用2列

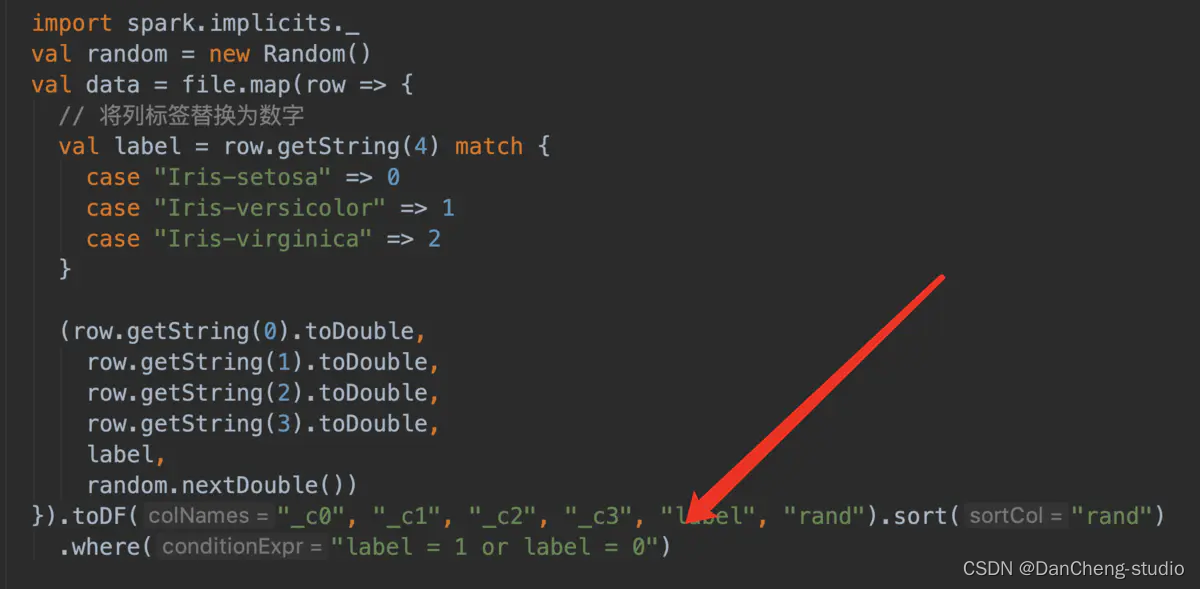
计算结果

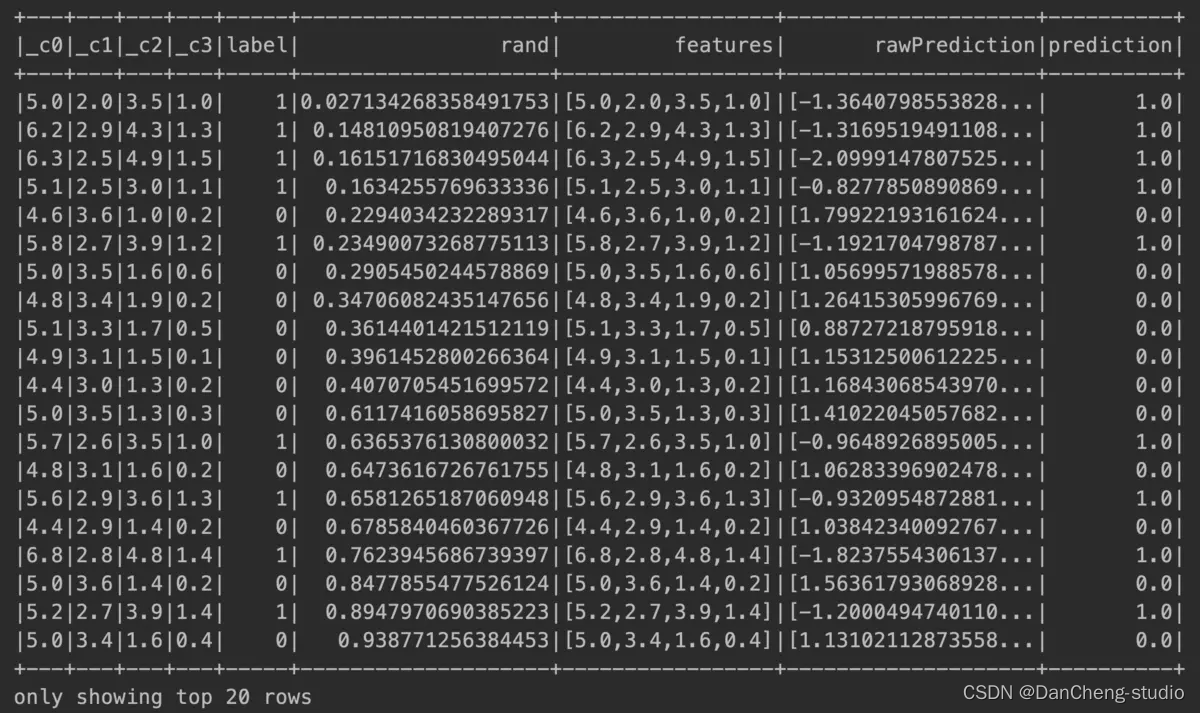
3 决策树算法

3.1 决策树介绍

• 决策树因其进行决策判断的结构与数据结构中的树相同,故而得名

• 决策树算法既可以实现分类,也可以实现回归, 一-般用作分类的比较多
  例如if-then就是一种简单的决策树

• 决策树的解法有很多
  例如ID3,C4.5等,其使用了信息论中熵的概念

3.2 决策树的缺点

• 对输入特征要求较高,很多情况下需要作预处理
• 识别类别过多时,发生错误的概率较大

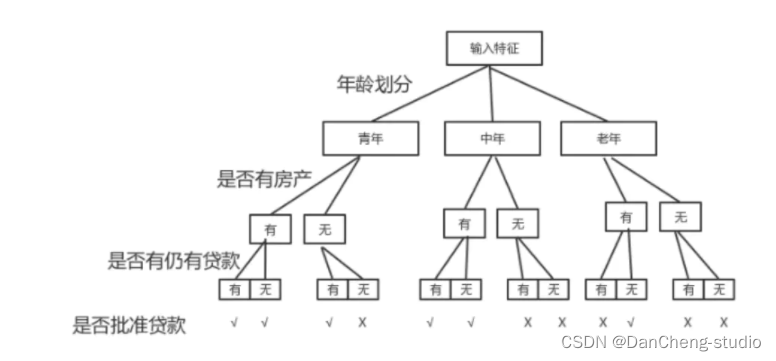
3.3 决策树示例

• 如图展示了一个能否批准贷款的决策树

3.4 决策树的特征选择

• 输入变量的特征有很多,选择特征作为分类判断的依据之一便是能够具有很好的区分度

• 那么也就是说,选择出的变量能够更具有代表性,以至于区分程度更高,作为决策树的判断节点

3.5 决策树的剪枝

• 决策树是针对训练集进行递归生成的,这样对于训练集效果自然非常好,但是对未知数据的预测结果可能并不会很好

• 即使用决策树生成算法生成的决策树模型过于复杂,对未知数据的泛化能力下降,即出现了过拟合现象

• 过拟合是因为树的结构过于复杂,将树的结构精简,就能够减轻过拟合现象,即决策树的剪枝

• 决策树从叶节点开始递归地向根节点剪枝

• 判断一个节点能否被减掉,只需比较修剪后与修剪前的损失函数值大小即可

• 如果在修剪之后,损失函数值小于等于原先的损失函数值,则将该父节点变为新的叶节点即可

3.6 CART算法

• CART即分类与回归决策树,其实是一棵二叉树,根据判断结果划分为”是否”二分类

决策树生成
基于训练集生成 一个尽可能大的决策树

决策树剪枝
使用验证集对生成的决策树进行剪枝,以便使损失函数最小化

3.7 决策树代码实战

决策树是一种流行的分类和回归方法。有关spark.ml实现的更多信息可以在决策树的部分中找到。

示例，以下示例以LibSVM格式加载数据集，将其拆分为训练和测试集，在第一个数据集上训练，然后评估保持测试集。我们使用两个特征变换器来准备数据;这些帮助标记和分类特征的索引类别，向决策树算法可识别的DataFrame添加元数据。

import org.apache.spark.ml.Pipeline
import org.apache.spark.ml.classification.DecisionTreeClassificationModel
import org.apache.spark.ml.classification.DecisionTreeClassifier
import org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator
import org.apache.spark.ml.feature.{IndexToString, StringIndexer, VectorIndexer}

// Load the data stored in LIBSVM format as a DataFrame.
val data = spark.read.format("libsvm").load("data/mllib/sample_libsvm_data.txt")

// Index labels, adding metadata to the label column.
// Fit on whole dataset to include all labels in index.
val labelIndexer = new StringIndexer()
  .setInputCol("label")
  .setOutputCol("indexedLabel")
  .fit(data)
// Automatically identify categorical features, and index them.
val featureIndexer = new VectorIndexer()
  .setInputCol("features")
  .setOutputCol("indexedFeatures")
  .setMaxCategories(4) // features with > 4 distinct values are treated as continuous.
  .fit(data)

// Split the data into training and test sets (30% held out for testing).
val Array(trainingData, testData) = data.randomSplit(Array(0.7, 0.3))

// Train a DecisionTree model.
val dt = new DecisionTreeClassifier()
  .setLabelCol("indexedLabel")
  .setFeaturesCol("indexedFeatures")

// Convert indexed labels back to original labels.
val labelConverter = new IndexToString()
  .setInputCol("prediction")
  .setOutputCol("predictedLabel")
  .setLabels(labelIndexer.labels)

// Chain indexers and tree in a Pipeline.
val pipeline = new Pipeline()
  .setStages(Array(labelIndexer, featureIndexer, dt, labelConverter))

// Train model. This also runs the indexers.
val model = pipeline.fit(trainingData)

// Make predictions.
val predictions = model.transform(testData)

// Select example rows to display.
predictions.select("predictedLabel", "label", "features").show(5)

// Select (prediction, true label) and compute test error.
val evaluator = new MulticlassClassificationEvaluator()
  .setLabelCol("indexedLabel")
  .setPredictionCol("prediction")
  .setMetricName("accuracy")
val accuracy = evaluator.evaluate(predictions)
println(s"Test Error = ${(1.0 - accuracy)}")

val treeModel = model.stages(2).asInstanceOf[DecisionTreeClassificationModel]
println(s"Learned classification tree model:\n ${treeModel.toDebugString}")

4 最后-毕设帮助