【手敲算法】树状数组[模板] 理解 到 裸敲

为什么学树状数组

每次修改一段区间，O(n) 根本不能满足我们对时间复杂度的需求

有需求就要有解决的办法

算法作用

维护一段线性区间的 O(logn) 的更新与查询

算法原理

为了理解，我们从目的 =>倒推 =>方法：

因为要 O(logn) 的查询长度，所以可以将一个线段分成最长为 logn 的很多段

每段为了计算长度，则会继续向下递归分解。

那么遵循一种分解规则，将线段分段，查一大段的时候，如果它切割的一小段已经有sum值，那么直接加上这个值，

然后跳过这段，这样就加快了查询的速度。

如此一来，修改一个点 也只需要逐层 将包含这一点的线段 都修改一遍即可

 

现在我们就来说说切割原理

一个int数字，转换为二进制的 0 1 串，

如：10101110000

它最多有 logn 个 sum(0 or 1) —————— 这正好符合我们对于切割线段的需求

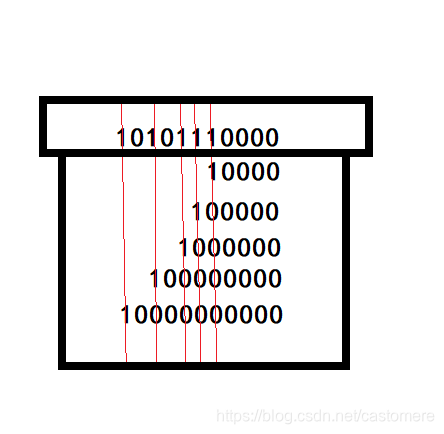
所以转换成二进制后，每次我们这样切割这个数字

发现下半部分的sum 等于上面的数字

这个操作就相当于 取最后一个1 + 后面全0后缀

代码内使用 lowbit 的操作可得。

修改操作：

一个 1000 二进制数字（线段）包含在后面 所有二进制第四位为1 的数字（线段）中，所以每次修改都要把这些数字代表的线段都修改

总结代码操作：

const int maxn = (int)1e5 + 5;
int n, a[maxn], c[maxn];
int lowbit(int x){
	return x & (-x);
}

int sum(int x){
	int res = 0;
	while(x){
		res += c[x];
		x -= lowbit(x);
	}
	return res;
}

void add(int x, int v){
	while(x < maxn){
		c[x] += v;
		x += lowbit(x);
	}
}

 这里的sum是求 [ 1，x ] 的和，既前缀和

add是单点x 加v

区间修改的树状数组：

需求：

修改的需求                              ——  区间 [ L , R ] 内 每个数字加上 v

区间查询需求                          ——  区间 [ L , R ] 内数字的 sum

原理：

对一段区间 [L, R] 加上 v 就是对 原数组 a ， a[L] + v , a[L+1] + v , --- a[R] + v

又陷入了逐个添加的窘境.

 

为了解决，引入一个增量数组 del[maxn]，

对 [L , R] 的操作 转化为:

1. del[L] 增量 + v , 代表 [L ~~ n] 区间 每个数字 + v

2. del[R+1] 增量  + (-v) ,代表 [R + 1 ~~ n] 区间 每个数组 + (-v)

预处理前缀和保存在a数组中 ，del[i] 对 sum[x] （增量前缀和）的贡献值为 del[i] * (x - i  + 1) ，那么

sum[x] = a[x] + del[1] * x + del[2] * (x-1) + del[3] * (x-2) + ... + del[x] * 1

           = a[x] + Σ( del[i] * (x - i + 1) )

           = a[x] + (x+1) * Σdel[i] - Σ(del[i] * i)      (1 <= i <= x)

由此得出更新 与 查询的操作

const int maxn = (int)1e5 + 5;
int n, a[maxn], del[maxn], c[maxn];
int lowbit(int x){
	return x & (-x);
}

// 前缀和
void PreSum(){
	for(int i = 1 ; i <= n ; i++)	a[i] += a[i-1];
}

int sum(int *arr, int x){
	int res = 0;
	while(x){
		res += arr[x];
		x -= lowbit(x);
	}
	return res;
}

void add(int *arr, int x, int v){
	while(x < maxn){
		arr[x] += v;
		x += lowbit(x);
	}
}

int query(int L, int R, int v){
	int ans = a[R] - a[L-1];
	ans += ( (R+1) * sum(del, R) - sum(c, R) );
	ans -= ( L *sum(del, L-1) - sum(c, L-1) );
	return ans;
}

int updata(int L, int R, int v){
	add(del, L, v);
	add(del, R+1, -v);
	add(c, L, L*v);
	add(c, R+1, -(R+1)*v);
}

线段树也能实现区间的增删改查，但是树状数组代码简单，代码量明显少于线段树

如果能数量掌握，对于仅需要对线段进行简单处理的题目，可以提高书写速度