搜索树之B-/B+树的特性与实现

现代计算机中，在内存与外存(磁盘)组成的二级存储系统中， 数据全集往往存放于外存中，计算过程中则可将内存作为外存的高速缓存，存放最常用数据项的复本。借助高效的调度算法，如此便可将内存的“高速度”与外存的“大容量”结合起来。
两个相邻存储级别之间的数据传输，统称I/O操作。各级存储器的访问速度相差悬殊，故应 尽可能地减少I/O操作。仍以内存与磁盘为例，其单次访问延迟大致分别在纳秒(ns)和毫秒(ms) 级别，相差5至6个数量级。也就是说，对内存而言的一秒/一天，相当于磁盘的一星期/两千年。 因此，为减少对外存的一次访问，我们宁愿访问内存百次、千次甚至万次。也正因为此，在衡量相关算法的性能时，基本可以忽略对内存的访问，转而更多地关注对外存的访问次数。

多路搜索树

当数据规模大到内存已不足以容纳时，常规平衡二叉搜索树的效率将大打折扣。其原因在于，查找过程对外存的访问次数过多。
例如，若将10^9个记录在外存中组织为AVL树，则每次查找大 致需做30次外存访问。那么，如何才能有效减少外存操作呢?
为此，需要充分利用磁盘之类外部存储器的另一特性: 就时间成本而言，读取物理地址连续 的一千个字节，与读取单个字节几乎没有区别。
既然外部存储器更适宜于批量式访问，不妨通过 时间成本相对极低的多次内存操作，来替代时间成本相对极高的单次外存操作。相应地，需要将 通常的二叉搜索树，改造为多路搜索树—在中序遍历的意义下，这也是一种等价变换。

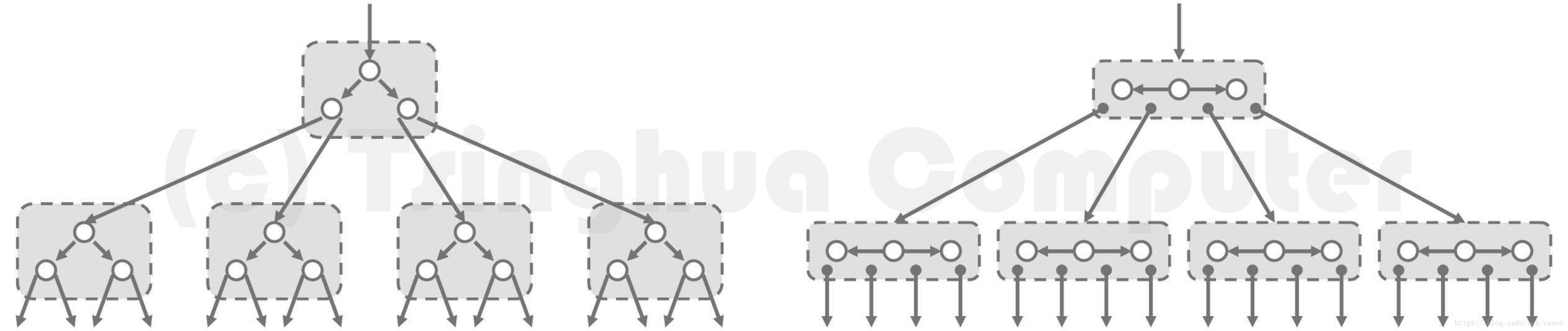
具体地如上图所示，比如可以两层为间隔，将各节点与其左、右孩子合并为“大节点”:

• 原节点及其孩子的共三个关键码予以保留;
• 孩子节点原有的四个分支也予以保留并按中序遍历次序排列;
• 节点到左、右孩子的分支转化为“大节点”内部的搜索，在图中表示为水平分支。

如此改造之后，每个“大节点”拥有四个分支，故称作四路搜索树。

这一策略还可进一步推广，比如以三层为间隔，将各节点及其两个孩子、四个孙子合并为含 有七个关键码、八个分支的“大节点”，进而得到八路搜索树。一般地，以k层为间隔如此重组， 可将二叉搜索树转化为等价的2^k路搜索树，统称多路搜索树(multi-way search tree)，亦趁为m（m>=2）路平衡搜索树。

多路搜索树同样支持查找等操作，且效果与原二叉搜索树完全等同;
然而重要的是，其对外存的访问方式已发生本质变化。实际上，在此时的搜索每下降一层，都以“大节点” 为单位从外存读取一组(而不再是单个)关键码。更为重要的是，这组关键码在逻辑上与物理上都彼此相邻，故可以批量方式从外存一次性读出，且所需时间与读取单个关键码几乎一样。