Java中关于单链表中环的入口与环的长度问题记录

最新推荐文章于 2022-10-24 20:33:51 发布

guopengxia0719_study

最新推荐文章于 2022-10-24 20:33:51 发布

阅读量487

点赞数

CC 4.0 BY-SA版权

分类专栏：数据结构学习笔记

本文链接：https://blog.youkuaiyun.com/cainiao_study/article/details/99982819

数据结构学习笔记专栏收录该内容

1 篇文章

订阅专栏

本文详细解析了链表中环的检测方法，利用快慢指针判断链表是否存在环，计算环的长度，并精确找到环的入口节点。通过具体示例和Java代码实现，展示了完整的环检测和入口定位过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

首先，需要明确的几个点（后面会有分析及代码）：

1.链表中是否有环，这个可以根据快慢指针

2.链表中环的长度，这个是慢指针走到相遇点的长度

3.确定环的入口点，这个是根据相遇点到环的入口和从头节点到环的入口处长度一致，计算出再次相遇的节点即为入口点

此次是看了众多博客后进行的总结记录，方便以后学习，不过不再进行证明，仅是说明和完整的Java代码实现部分

举例说明：

再进行跑步比赛时，A,B两个人，A的速度是x,B的速度是2x,则可以得出，A,B会在起点相遇，并且A跑1圈，B跑2圈

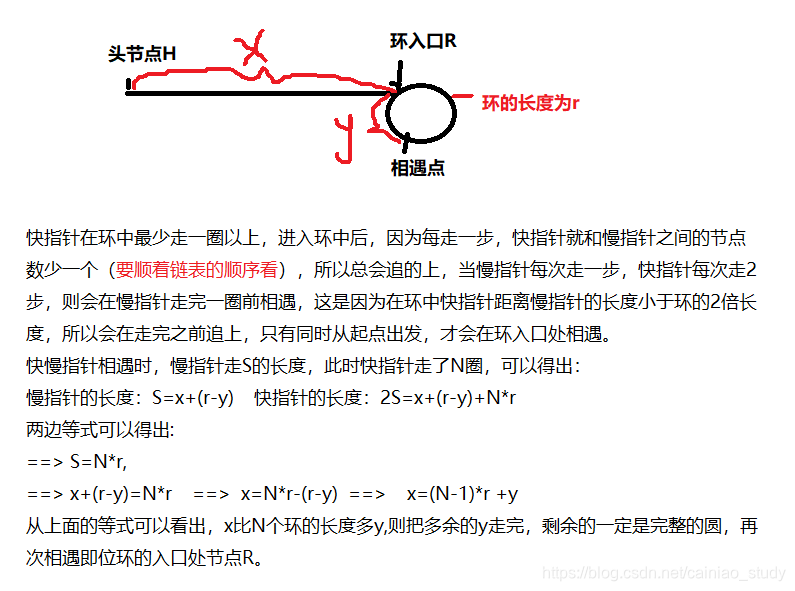
以上是针对图中x的长度小于环的长度的情况，基于此种情况进行假设证明，

对于链表中环的计算方式，B会在A没走完一圈时就会追赶上，追上的情况需满足的条件时：有环，快指针比慢指针快一个节点

快指针在环中追上的慢指针，以上条件是基于环的长度比头节点到环的入口节点长度要长的情况下进行处理的。

对于环的长度大于头节点到环入口节点的长度，即x的长度一定大于y的长度的情况，

代码实现如下所示：

实例所用数据为：

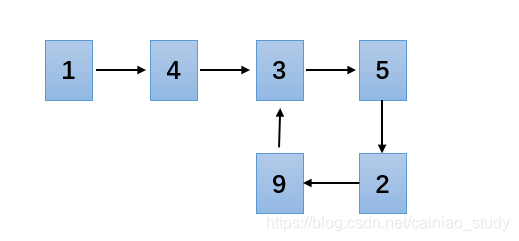
代码部分：

节点的类：

package com.gx.fifteen.class01;

class Node {
    Node next;
    int data;

    public Node(int data, Node next) {
        this.next = next;
        this.data = data;
    }
}

实现的类：

package com.gx.fifteen.class01;

public class CircleListTest {

    public Node getNodeList(){
        Node six=new Node(9,null);
        Node five=new Node(2,six);
        Node four=new Node(5,five);
        Node three=new Node(3,four);
        Node two=new Node(4,three);
        Node head=new Node(1,two);
        six.next=three;  //形成环
        return head;
    }

    public void showList(Node head){
        while(head!=null){
            System.out.print(head.data+"  ");
            head=head.next;
        }
    }

    //判断是否有环的操作
    public boolean isLoop(Node head){
        Node fast=head;
        Node slow=head;
        if(fast==null){
            return false;
        }
        while(fast !=null && fast.next !=null){
            fast=fast.next.next;
            slow=slow.next;
            if(fast == slow){
                System.out.println("该链表有环");
                System.out.println("相遇的数据是："+slow.data);
                return true;
            }
        }
        System.out.println("链表没有环");
        return !(fast == null || fast.next ==null);
    }

    //判断链表环的入口
    public Node findLoopPort(Node head){
        Node fast=head;
        Node slow=head;
        while(fast!=null && fast.next!=null){
            slow=slow.next;
            fast=fast.next.next;
            if(fast==slow)break;
        }
        if(fast ==null || fast.next ==null){
            return  null;
        }
        slow=head;
        while(slow !=fast){
            slow=slow.next;
            fast=fast.next;
        }
        return slow;
    }

    public static void main(String []args){
        CircleListTest clt=new CircleListTest();
        Node head=clt.getNodeList();
        //System.out.println("链表输出结果为：");
        //clt.showList(head);
        clt.isLoop(head);
        Node ring=clt.findLoopPort(head);
        System.out.println("环的入口是："+ring.data);
    }
}

运行结果为：

该链表有环
相遇的数据是：2
环的入口是：3