查找算法（线性，二分法，插值，黄金分割）

1.线性查找算法介绍：

        线性查找又称顺序查找，是一种最简单的查找方法，它的基本思想是从第一个记录开始，逐个比较记录的关键字，直到和给定的K值相等，则查找成功；

2.代码实现：

package select;

/**
 * @author WuChenGuang
 */
public class LinearSelect {
    public static void main(String[] args) {
        /*
          查询该数组下是否存在9这个元素，如果存在则返回索引值，否则返回-1
          1.线性查找
         */
        int[] array = new int[]{2, 4, 8, 6, 4, 9, 0};
        int i = show(array, 10);
        System.out.println(i);
    }

    public static int show(int[] array, int target) {
        for (int i = 0; i < array.length; i++) {
            if (array[i] == target) {
                return i;
            }
        }
        return -1;
    }
}

运行结果：

3.二分法查找算法介绍：

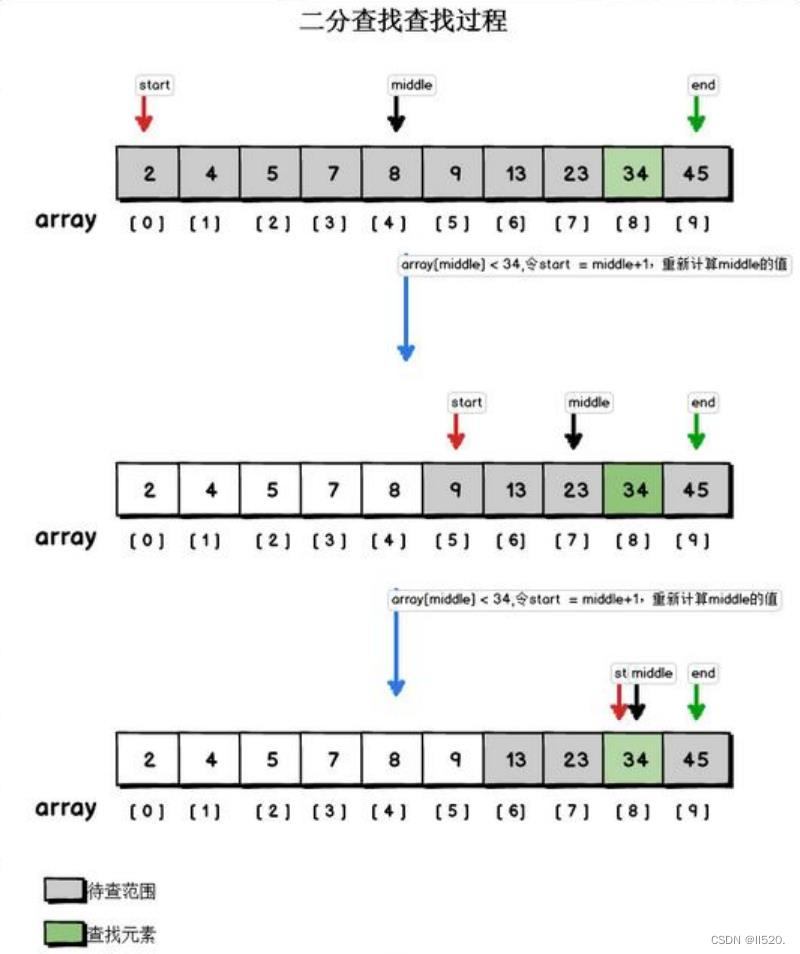
        二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。

示意图：

 4.代码实现：

package select;

/**
 * @author WuChenGuang
 */
public class BinarySearch {
    public static void main(String[] args) {

        int[] array = new int[]{10, 11, 12, 13, 14, 15, 16, 17};
        int target = 10;

        int index = search(array, target);
        System.out.println(index);
    }

    public static int search(int[] array, int target) {
        // 最小索引指针
        int min = 0;
        int max = array.length - 1;

        while (min <= max) {
            // 算出平均索引位置
            int mid = (min + max) / 2;
            if (array[mid] == target) {
                return mid;
            }
            if (array[mid] < target) {
                min = mid + 1;
            }
            if (array[mid] > target) {
                max = mid - 1;
            }
        }
        return -1;
    }
}

运行结果：

5.插值查找算法介绍：

        插值查找，有序表的一种查找方式。插值查找是根据查找关键字与查找表中最大最小记录关键字比较后的查找方法。插值查找基于二分查找，将查找点的选择改进为自适应选择，提高查找效率。

示意图：

 

解释：当我们从字典中查找 “algorithm” 这个单词的时候，我们肯定不会傻傻地像二分查找一样首先从中间开始。相反，我们会从首字母为 a 的地方开始查找，然后根据第二个字母在字母表中的位置，找到相应的位置再继续查找，这样重复这个过程，直到我们查找到这个单词。

6.代码实现：

package select;

/**
 * @author WuChenGuang
 */
public class InsertSelect {
    public static void main(String[] args) {

        int[] array = {1, 2, 3, 4, 5, 6};

        int left = 0;
        int right = array.length - 1;

        int searchVal = 1;
        System.out.println(select(array, left, right, searchVal));
    }

    public static int select(int[] array, int left, int right, int searchVal) {

        // 防止数组越界
        if (left > right || searchVal < array[0] || searchVal > array[array.length - 1]) {
            return -1;
        }

        int mid = left + (right - left) * (searchVal - array[left]) / (array[right] - array[left]);
        int midValue = array[mid];
        if (searchVal > midValue) {
            return select(array, mid + 1, right, searchVal);
        } else if (searchVal < midValue) {
            return select(array, left, mid - 1, searchVal);
        } else {
            return mid;
        }
    }
}

运行结果：

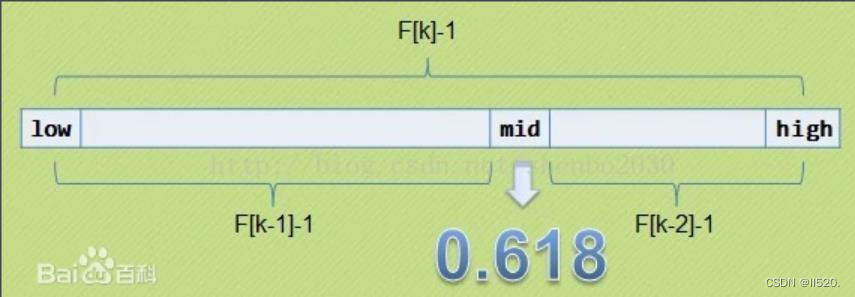
 7.黄金分割法算法（斐波那契算法）

        在介绍斐波那契查找算法之前，先介绍一下很它紧密相连的一个概念——黄金分割。黄金比例又称黄金分割，是指事物各部分间一定的数学比例关系，即将整体一分为二，较大部分与较小部分之比等于整体与较大部分之比，其比值约为1:0.618或1.618:1。因此被称为黄金分割。斐波那契数列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…….（从第三个数开始，后边每一个数都是前两个数的和）。然后我们会发现，随着斐波那契数列的递增，前后两个数的比值会越来越接近0.618，利用这个特性，我们就可以将黄金比例运用到查找技术中。

 8.代码实现：

package select;

import java.util.Arrays;

/**
 * @author WuChenGuang
 */
public class FibonacciSelect {
    public static void main(String[] args) {

        int[] array = {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89};
        System.out.println(select(array, 13));
    }

    /**
     * f[k] = (f[k-1])+ (f[k-2])
     */
    public static int[] f() {
        int[] f = new int[20];
        f[0] = 1;
        f[1] = 1;
        for (int i = 2; i < f.length; i++) {
            f[i] = f[i - 1] + f[i - 2];
        }
        return f;
    }


    /**
     * mid = low+F(k-1)-1
     */
    public static int select(int[] array, int key) {

        int low = 0;
        int high = array.length - 1;
        int k = 0;
        int mid;
        int[] f = f();

        // 找分割点
        while (high > f[k] - 1) {
            k++;
        }

        int[] temp = Arrays.copyOf(array, f[k]);

        // {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89} --> {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89，89,89,}
        for (int i = high + 1; i < temp.length; i++) {
            temp[i] = array[high];
        }

        while (low <= high) {
            mid = low + f[k - 1] - 1;

            // f[k-1]+f[k-2] = f[k];
            if (key < temp[mid]) {
                high = mid - 1;
                k--;
            } else if (key > temp[mid]) {
                low = mid + 1;
                k -= 2;
            } else {
                return Math.min(mid, high);
            }
        }
        return -1;
    }
}

运行结果：