机器学习中的分类问题和回归问题的性能评估指标

0、分类问题和回归问题的区别

  预测建模是使用已知数据的模型对没有标签或结果的新数据进行预测的过程。

  预测建模可以理解为找到一个最佳映射函数$f(x)$ 逼近于输入变量$X$的真实分布$y$的过程。所以，可以将所有的逼近任务分为分类任务和回归任务。

  分类问题和回归问题对真实世界的预测建模方法不同。

  分类预测建模是用映射函数$f(x)$对输入变量$X$近似地预测出离散输出变量$y$的任务。

  回归预测建模是用映射函数$f(x)$对输入变量$X$近似地预测出连续输出变量$y$的任务。

  通俗的说：

• 分类是对离散类样本的标签进行预测（例如，判断照片中人的性别、判断邮件是垃圾邮件还是有用的邮件、海中不同的船只的类别预测）。
• 回归问题是对连续类的数量进行预测（例如，预测明天下雨的概率、预测北京的房价、预测人体的身高范围等等）。

1、评估分类问题的性能指标（classification）

  分类问题是监督类学习（supervision learning）的一个重要问题。在机器学习中主要分两大类：

• 通过从已知标签的样本中学习到一个分类器（分类决策函数，分类超平面）。
• 用该分类器对新的样本的类别进行预测。

  评估一个分类器的好坏包括许多项指标。在实际应用中选择正确的评估方法是十分重要的。下面就一一列举一些评价分类问题好坏的性能指标。

1、混淆矩阵

  假设是二分类问题，计为正例（positive） 和 负例（negative） 分别是：

• $\text{True positives(TP)}$：真正，实际为正例且被分类器划分为正例的实例数（划分正确）。
• $\text{False positives(FP)}$：假正，实际为负例但被分类器划分为正例的实例数（划分错误）。
• $\text{False negatives(FN)}$：假负，实际为正例但被分类器划分为负例的实例数（划分错误）。
• $\text{True negatives(TN)}$：真负，实际为负例且被分类器划分为负例的实例数（划分正确）。

  所以，上述过程可以用混淆矩阵来表示：

  上面的表示方法和混淆矩阵中，$T$和$F$代表该判别是对的还是错的（true false），$P$和$N$代表这个样本是正的还是负的。

2、准确率（Accuracy）

  准确率是分类器分类正确的样本数量与样本总数的比：

$$\text{Accuracy}=\frac{TP+TN}{TP+TN+FP+FN},$$

该公式反映了分类器对整个样本的判定能力，即能够将正的判定为正，负的判定为负。

3、错误率（Error）

  错误率（Error）则正好与准确率的含义相反，计算公式如下：

$$\text{Error}=\frac{FP+FN}{TP+TN+FP+FN}.$$

4、精准率（Precision）

  精准率是指即被分类器判定为正类样本中真正的正类样本所占的比重，公式如下：

$$\text{Precision}=\frac{TP}{TP+FP},$$

该公式只针对于所有被分类器分类为正类的样本。

5、召回率（Recall）

  召回率（Recall）是指被分类器正确判定的正类样本占总的正类样本的比重。计算公式如下：

$$\text{Recall}=\frac{TP}{TP+FN}$$

6、F-score

  精确率和召回率反映了分类器性能的两个不同方向。一般情况下，精确率越高，召回率越低，而召回率越高，精确率越低。所以依靠单独某个指标并不能较为全面的评价一个分类器的性能。为了较为全面的评价一个分类器，平衡精确率和召回率的影响，引入了$\text{F-score}$这个综合指标。

  $\text{F-score}$是精确率和召回率的调和均值，计算公式如下：

$$\begin{array}{rl}{F}_{\beta }& =(1+{\beta }^2)\frac{\text{Precision}\times \text{Recall}}{{\beta }^2\times \text{Precision}+\text{Recall}}\\ & =(1+{\beta }^2)\frac{(1+{\beta }^2)\text{TP}}{{\beta }^2\times \text{TP}+{\beta }^2\text{FP}+\text{FN}}\end{array}$$

其中， $\beta (\beta >0)$的取值反映了精确率和召回率在性能评估中的相对重要性，通常情况下取值为$1$。

  当$\beta =1$时，就是常用的${\text{F}}_1$值，表明精确率和召回率的重要性是一样的。计算公式如下：

$$\frac{2}{{\text{F}}_1}=\frac{1}{\text{Precision}}+\frac{1}{\text{Recall}},$$

则有，

$$\begin{array}{rl}{\text{F}}_1& =\frac{2\times \text{Precison}\times \text{Recall}}{\text{Precison}+\text{Recall}}\\ & =\frac{2\times \text{TP}}{2\times \text{TP}+\text{FP}+\text{FN}}.\end{array}$$

  ${\text{F}}_1$又称为平衡$\text{F}$分数。精确率和召回率都高时， ${\text{F}}_1$也会高。

  当$\beta =2$时，$F_2$表明召回率的权重比精确率高。

  当$\beta =0.5$时，$F_{0.5}$表明精确率的权重比召回率高。

  以上讨论的评估指标仅适用于二分类问题，当问题属于多分类问题时，在不同类别下综合考察分类器的优劣就需要引入宏平均（$\text{Macro-averaging}$）、微平均（$\text{Micro-averaging}$）。

7、平均（Averaging）

1、宏平均（Macro-averaging）

  宏平均（Macro-averaging）是指所有类别的每一个统计指标值的算数平均值，也就是宏精确率（Macro-Precision），宏召回率（Macro-Recall），宏F值（Macro-F Score），其计算公式如下：

$${\text{Precision}}_{\text{macro}}=\frac{1}{n}\sum _{i=1}^n{\text{P}}_i$$

$${\text{Recall}}_{\text{macro}}=\frac{1}{n}\sum _{i=1}^n{\text{R}}_i$$

$${\text{F}}_{\text{macro}}=\frac{2\times {\text{P}}_{\text{macro}}\times {\text{R}}_{\text{macro}}}{{\text{P}}_{\text{macro}}+{\text{R}}_{\text{macro}}}$$

2、微平均（Micro-averaging）

  微平均（Micro-averaging）是对数据集中的每一个示例不分类别进行统计建立全局混淆矩阵，然后计算相应的指标。

  Macro-averaging与Micro-averaging的不同之处在于：Macro-averaging赋予每个类相同的权重，然而Micro-averaging赋予每个样本决策相同的权重。因为从$F_1$值的计算公式可以看出，它忽略了那些被分类器正确判定为负类的那些样本，它的大小主要由被分类器正确判定为正类的那些样本决定的，在微平均评估指标中，样本数多的类别主导着样本数少的类。

7、P-R曲线

  PR曲线是$\text{Precision Recall Curve}$的简称，描述的是precision和recall之间的关系，以recall为横坐标，precision为纵坐标绘制的曲线。

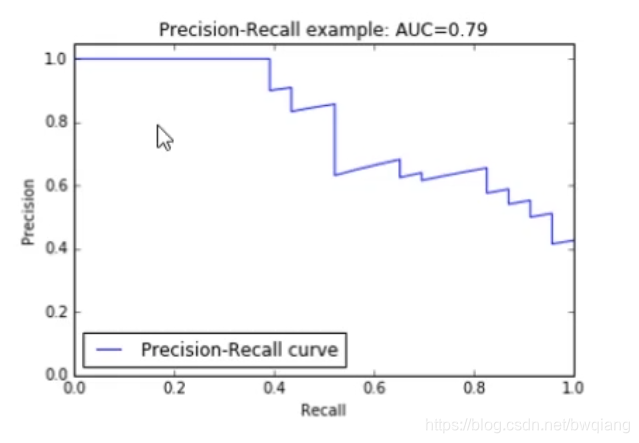
  由图可见，如果提高召回率，则精确率会受到影响而下降。

8、ROC曲线

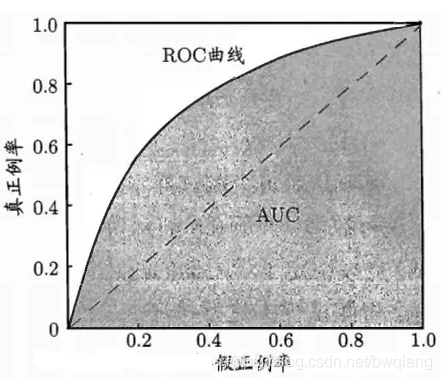
  ROC曲线全称为 受试者工作特征（Receiver Operating Characteristic）曲线。以灵敏度（真阳性率）为纵坐标，以1减去特异性（假阳性率）为横坐标绘制的性能评价曲线

  也可理解为：我们根据学习器的预测结果，把阈值从$0$变到最大，即刚开始是把每个样本作为正例进行预测，随着阈值的增大，学习器预测正样例数越来越少，直到最后没有一个样本是正样例。在这一过程中，每次计算出TP和FP，分别以它们为横、纵坐标作图，就得到了“ROC曲线”。

  ROC曲线的纵轴是“真正率”(True Positive Rate, 简称TPR)，真正正例占总正例的比例，反映命中概率。横轴是“假正率”(False Positive Rate,简称FPR)，错误的正例占负例的比例，反映误诊率、假阳性率、虚惊概率等等。

9、AUC（area under curve）

  AUC就是ROC曲线下的面积，即ROC的积分。衡量学习器优劣的一种性能指标。

  AUC的取值范围为$[0,1]$。

  AUC是衡量二分类模型优劣的一种评价指标，表示预测的正例排在负例前面的概率（反映分类器对样本的排序能力）。

  AUC提供了分类器的一个整体数值。通常AUC越大，分类器越好。

  三种AUC值示例：

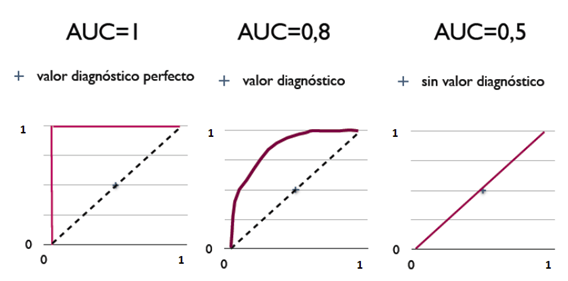
  从AUC判断分类器（预测模型）优劣的标准：

• AUC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器。
• 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
• AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
• AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

2、评估回归问题的性能指标（Regression）

  回归问题的典型性能指标是均方根误差（RMSE），它测量的是预测过程中预测错误的标准偏差（标准偏差是方差的算术平方根，而方差是离均平方差的平均数）。

  计算公式如下：

$$\text{RMSE}(X,h)=\sqrt{\frac{1}{m}\sum _{i=1}^m(h(X^{(i)})-y^{(i)}{)}^2}$$

其中：

• $m$是$\text{RMSE}$数据集中实例的个数。
• $X^{(i)}$是数据集第$i$个实例的所有特征值的向量，$y^{(i)}$是它的标签。
• $h$是系统的预测函数，也称为假设。当系统收到一个实例的特征向量X^{(i)}，就会输出这个实例的一个预测值$\tilde{y}=h(X^{(i)})$

  有关分类问题和其余的回归问题的损失函数的定义和其含义，见下篇博文《机器学习的分类问题和回归问题的损失函数》，to be continued…