51 序列模型_by《李沐：动手学深度学习v2》pytorch版

系列文章目录

---

---

一、理论知识

序列模型

想象一下有人正在看网飞（Netflix，一个国外的视频网站）上的电影。
一名忠实的用户会对每一部电影都给出评价，毕竟一部好电影需要更多的支持和认可。然而事实证明，事情并不那么简单。
随着时间的推移，人们对电影的看法会发生很大的变化。事实上，心理学家甚至对这些现象起了名字：

• 锚定（anchoring）效应：基于其他人的意见做出评价。
  例如，奥斯卡颁奖后，受到关注的电影的评分会上升，尽管它还是原来那部电影。
  这种影响将持续几个月，直到人们忘记了这部电影曾经获得的奖项。
  结果表明（ :cite:Wu.Ahmed.Beutel.ea.2017），这种效应会使评分提高半个百分点以上。
• 享乐适应（hedonic adaption）：人们迅速接受并且适应一种更好或者更坏的情况
  作为新的常态。
  例如，在看了很多好电影之后，人们会强烈期望下部电影会更好。
  因此，在许多精彩的电影被看过之后，即使是一部普通的也可能被认为是糟糕的。
• 季节性（seasonality）：少有观众喜欢在八月看圣诞老人的电影。
• 有时，电影会由于导演或演员在制作中的不当行为变得不受欢迎。
• 有些电影因为其极度糟糕只能成为小众电影。Plan9from Outer Space和Troll2就因为这个原因而臭名昭著的。

简而言之，电影评分决不是固定不变的。因此，使用时间动力学可以得到更准确的电影推荐 :cite:Koren.2009。
当然，序列数据不仅仅是关于电影评分的。下面给出了更多的场景。

• 在使用程序时，许多用户都有很强的特定习惯。
  例如，在学生放学后社交媒体应用更受欢迎。在市场开放时股市交易软件更常用。
• 预测明天的股价要比过去的股价更困难，尽管两者都只是估计一个数字。
  毕竟，先见之明比事后诸葛亮难得多。
  在统计学中，前者（对超出已知观测范围进行预测）称为外推法（extrapolation），
  而后者（在现有观测值之间进行估计）称为内插法（interpolation）。
• 在本质上，音乐、语音、文本和视频都是连续的。
  如果它们的序列被我们重排，那么就会失去原有的意义。
  比如，一个文本标题“狗咬人”远没有“人咬狗”那么令人惊讶，尽管组成两句话的字完全相同。
• 地震具有很强的相关性，即大地震发生后，很可能会有几次小余震，
  这些余震的强度比非大地震后的余震要大得多。
  事实上，地震是时空相关的，即余震通常发生在很短的时间跨度和很近的距离内。
• 人类之间的互动也是连续的，这可以从微博上的争吵和辩论中看出。

统计工具

由于存在时序信息，我算$x_2$是需要通过$x_1$来计算的，表现为有个箭头从$x_1$指向了$x_2$。

RNN有反向传播，有时候存在这种反序，知道未来的事情，推理前面的情况。物理上不一定可行是因为真实世界中，未来是根据过去产生的而不是反着。

我们一般是给定前面t-1个数据，然后计算$x_t$的概率。这里面的f可以当作是个模型，在过去的t-1个数据上训练一个模型，来推测下一个数据。之前我们在CNN中是通过一个图片来训练，得到一个标号label，label和图片不是一个东西，现在是给定前面t-1个数据，推理第t个数据，我们对这种模型叫自回归模型。（自回归：自回归模型的核心思想是使用时间序列过去的值来预测未来的值。"自回归"意味着模型使用自身的过去值作为预测未来值的依据。）我们先使用数据中的前一部分来不断推理后面的数据。核心是给定前面的t-1个数据怎么计算第t个数据。

自回归模型

为了实现这个预测，训练时可以使用回归模型，仅有一个主要问题：输入数据的数量，
输入$x_{t-1},\dots ,x_1$本身因$t$而异。也就是说，输入数据的数量这个数字将会随着我们遇到的数据量的增加而增加，因此需要一个近似方法来使这个计算变得容易处理。本章后面的大部分内容将围绕着如何有效估计$P(x_t\mid x_{t-1},\dots ,x_1)$展开。
简单地说，它归结为以下两种策略。
第一种策略，假设在现实情况下相当长的序列$x_{t-1},\dots ,x_1$可能是不必要的，因此我们只需要满足某个长度为$\tau$的时间跨度，即使用观测序列$x_{t-1},\dots ,x_{t-\tau }$。当下获得的最直接的好处就是参数的数量总是不变的，至少在$t>\tau$时如此，这就使我们能够训练一个上面提及的深度网络。这种模型被称为自回归模型（autoregressive models），因为它们是对自己执行回归。

第二种策略，是保留一些对过去观测的总结$h_t$，并且同时更新预测${\hat{x}}_t$和总结$h_t$。这就产生了基于${\hat{x}}_t=P(x_t\mid h_t)$估计$x_t$，以及公式$h_t=g(h_{t-1},x_{t-1})$更新的模型。由于$h_t$从未被观测到，这类模型也被称为隐变量自回归模型（latent autoregressive models）。

这两种情况都有一个显而易见的问题：如何生成训练数据？一个经典方法是使用历史观测来预测下一个未来观测。显然，我们并不指望时间会停滞不前。然而，一个常见的假设是虽然特定值$x_t$可能会改变，但是序列本身的动力学不会改变。这样的假设是合理的，因为新的动力学一定受新的数据影响，而我们不可能用目前所掌握的数据来预测新的动力学。统计学家称不变的动力学为静止的（stationary）。因此，整个序列的估计值都将通过以下的方式获得：

$$P(x_1,\dots ,x_T)=\prod _{t=1}^{T}P(x_t\mid x_{t-1},\dots ,x_1).$$

注意，如果我们处理的是离散的对象（如单词），而不是连续的数字，则上述的考虑仍然有效。唯一的差别是，对于离散的对象，我们需要使用分类器而不是回归模型来估计$P(x_t\mid x_{t-1},\dots ,x_1)$。

方案A-马尔科夫假设

回想一下，在自回归模型的近似法中，我们使用$x_{t-1},\dots ,x_{t-\tau }$而不是$x_{t-1},\dots ,x_1$来估计$x_t$。使得我们不用处理变长的数据，然后只需要处理定长的数据，最简单的我们使用MLP就可以建模。只要这种是近似精确的，我们就说序列满足马尔可夫条件（Markov condition）。特别是，如果$\tau =1$，得到一个一阶马尔可夫模型（first-order Markov model），$P(x)$由下式给出：

$$P(x_1,\dots ,x_T)=\prod _{t=1}^{T}P(x_t\mid x_{t-1})\text{ 当 }P(x_1\mid x_0)=P(x_1).$$

当假设$x_t$仅是离散值时，这样的模型特别棒，因为在这种情况下，使用动态规划可以沿着马尔可夫链精确地计算结果。例如，我们可以高效地计算$P(x_{t+1}\mid x_{t-1})$：
$$\begin{array}{rl}P(x_{t+1}\mid x_{t-1})& =\frac{{\sum }_{x_t}P(x_{t+1},x_t,x_{t-1})}{P(x_{t-1})}\\ & =\frac{{\sum }_{x_t}P(x_{t+1}\mid x_t,x_{t-1})P(x_t,x_{t-1})}{P(x_{t-1})}\\ & =\sum _{x_t}P(x_{t+1}\mid x_t)P(x_t\mid x_{t-1})\end{array}$$

利用这一事实，我们只需要考虑过去观察中的一个非常短的历史：$P(x_{t+1}\mid x_t,x_{t-1})=P(x_{t+1}\mid x_t)$。隐马尔可夫模型中的动态规划超出了本节的范围，而动态规划这些计算工具已经在控制算法和强化学习算法广泛使用。

因果关系

原则上，将$P(x_1,\dots ,x_T)$倒序展开也没什么问题。
毕竟，基于条件概率公式，我们总是可以写出：

$$P(x_1,\dots ,x_T)=\prod _{t=T}^{1}P(x_t\mid x_{t+1},\dots ,x_T).$$

事实上，如果基于一个马尔可夫模型，我们还可以得到一个反向的条件概率分布。
然而，在许多情况下，数据存在一个自然的方向，即在时间上是前进的。
很明显，未来的事件不能影响过去。
因此，如果我们改变$x_t$，可能会影响未来发生的事情$x_{t+1}$，但不能反过来。
也就是说，如果我们改变$x_t$，基于过去事件得到的分布不会改变。
因此，解释$P(x_{t+1}\mid x_t)$应该比解释$P(x_t\mid x_{t+1})$更容易。
例如，在某些情况下，对于某些可加性噪声$ϵ$，显然我们可以找到$x_{t+1}=f(x_t)+ϵ$，而反之则不行。
而这个向前推进的方向恰好也是我们通常感兴趣的方向。
彼得斯等人对该主题的更多内容做了详尽的解释，而我们的上述讨论只是其中的冰山一角。

方案B-潜变量模型

上图中一个紫色的小圈，表示一个(小)模型。

总结

1. 时序模型中，当前数据跟之前观察到的数据相关
2. 自回归模型使用自身过去数据来预测未来
3. 马尔科夫模型假设当前只跟最近少数数据相关，从而简化模型
4. 潜变量模型使用潜变量来概括历史信息

二、代码：利用马尔可夫

import torch
from torch import nn
from d2l import torch as d2l

T = 1000  # 总共产生1000个点

# 创建一个从1到T（1000）的张量，dtype为float32
time = torch.arange(1, T + 1, dtype=torch.float32)

# 生成一个正弦波，并添加高斯噪声（均值为0，标准差为0.2）
# 0.01是正弦波的频率，time是时间序列
x = torch.sin(0.01 * time) + torch.normal(0, 0.2, (T,))

# 绘制时间序列图，x轴为时间，y轴为x的值
# xlim设置x轴的范围为1到1000，figsize设置图像的大小为6x3英寸
d2l.plot(time, [x], 'time', 'x', xlim=[1, 1000], figsize=(6, 3))

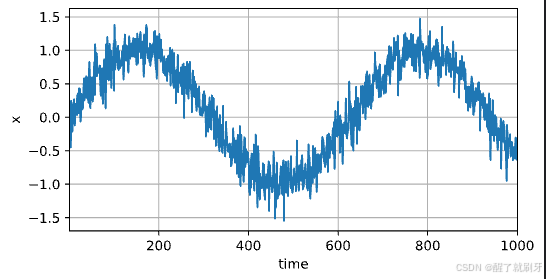
接下来，我们将这个序列转换为模型的特征－标签（feature-label）对。
基于嵌入维度$\tau$，我们[将数据映射为数据对$y_t=x_t$和${\mathbf{x}}_t=[x_{t-\tau },\dots ,x_{t-1}]$。]这比我们提供的数据样本少了$\tau$个，因为我们没有足够的历史记录来描述前$\tau$个数据样本。
一个简单的解决办法是：如果拥有足够长的序列就丢弃这几项；另一个方法是用零填充序列。在这里，我们仅使用前600个“特征－标签”对进行训练。

tau = 4  # 定义时间延迟（特征的数量），这里为4

# 创建一个形状为 (T - tau, tau) 的零张量，用于存储特征
features = torch.zeros((T - tau, tau))

# 填充特征张量
for i in range(tau):
    # 将信号 x 在时间延迟 i 处的切片存储到特征张量的第 i 列
    features[:, i] = x[i: T - tau + i]

# 创建标签张量，包含从第 tau 个元素开始到最后的信号值，并将其形状调整为 (N, 1)
labels = x[tau:].reshape((-1, 1))

batch_size, n_train = 16, 600  # 定义批量大小为16，训练样本数量为600

# 只使用前n_train个样本用于训练 使用 d2l.load_array 函数创建一个数据迭代器 train_iter，用于加载训练数据。
train_iter = d2l.load_array((features[:n_train], labels[:n_train]),
                             batch_size, is_train=True)

在这里，我们[使用一个相当简单的架构训练模型：一个拥有两个全连接层的多层感知机]，ReLU激活函数和平方损失。

# 初始化网络权重的函数
def init_weights(m):
    # 检查传入的模块是否为线性层
    if type(m) == nn.Linear:
        # 使用Xavier均匀分布初始化线性层的权重
        nn.init.xavier_uniform_(m.weight)

# 一个简单的多层感知机
def get_net():
    # 创建一个顺序模型，包括两个线性层和一个ReLU激活函数
    net = nn.Sequential(nn.Linear(4, 10),  # 输入层到隐藏层，4个输入，10个神经元
                        nn.ReLU(),       # 添加ReLU激活函数
                        nn.Linear(10, 1))  # 隐藏层到输出层，10个神经元，1个输出
    # 应用权重初始化函数
    net.apply(init_weights)
    return net  # 返回构建的网络

# 平方损失。注意：MSELoss计算平方误差时不带系数1/2
loss = nn.MSELoss(reduction='none')  # 创建均方误差损失函数，不进行任何聚合

# 定义训练函数
def train(net, train_iter, loss, epochs, lr):
    # 使用Adam优化器，设置学习率
    trainer = torch.optim.Adam(net.parameters(), lr)
    
    # 进行指定轮数的训练
    for epoch in range(epochs):
        # 遍历训练数据迭代器
        for X, y in train_iter:
            trainer.zero_grad()  # 清除之前的梯度
            # 计算当前批次的损失
            l = loss(net(X), y)
            l.sum().backward()  # 计算梯度
            trainer.step()  # 更新网络权重
            
        # 输出当前轮次的损失
        print(f'epoch {epoch + 1}, '
              f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}')

# 获取网络实例
net = get_net()

# 训练网络，指定训练轮数为50，学习率为0.01
train(net, train_iter, loss, 50, 0.01)

epoch 1, loss: 0.056556
epoch 2, loss: 0.054166
.....
epoch 49, loss: 0.050809
epoch 50, loss: 0.047008

主要看一下预测

由于训练损失很小，因此我们期望模型能有很好的工作效果。让我们看看这在实践中意味着什么。
首先是检查[模型预测下一个时间步]的能力，也就是单步预测（one-step-ahead prediction）。

# 使用训练好的网络对特征进行一次性预测 即给定四个数据，预测下面一个数据
onestep_preds = net(features)

# 绘制时间序列图
d2l.plot([time, time[tau:]],  # x轴为时间，包含原始时间和去掉前tau个点后的时间
         [x.detach().numpy(), onestep_preds.detach().numpy()],  # y轴为原始数据和一次性预测结果
         'time',  # x轴标签
         'x',  # y轴标签
         legend=['data', '1-step preds'],  # 图例，分别为原始数据和一次性预测
         xlim=[1, 1000],  # 设置x轴范围
         figsize=(6, 3))  # 设置图形大小为6x3英寸

正如我们所料，单步预测效果不错。
即使这些预测的时间步超过了$600+4$（n_train + tau），其结果看起来仍然是可信的。
然而有一个小问题：如果数据观察序列的时间步只到$604$，我们需要一步一步地向前迈进：
$$\begin{gathered} {\hat{x}}_{605}=f(x_{601},x_{602},x_{603},x_{604}), \\ {\hat{x}}_{606}=f(x_{602},x_{603},x_{604},{\hat{x}}_{605}), \\ {\hat{x}}_{607}=f(x_{603},x_{604},{\hat{x}}_{605},{\hat{x}}_{606}), \\ {\hat{x}}_{608}=f(x_{604},{\hat{x}}_{605},{\hat{x}}_{606},{\hat{x}}_{607}), \\ {\hat{x}}_{609}=f({\hat{x}}_{605},{\hat{x}}_{606},{\hat{x}}_{607},{\hat{x}}_{608}), \\ \dots \end{gathered}$$

通常，对于直到$x_t$的观测序列，其在时间步$t+k$处的预测输出${\hat{x}}_{t+k}$称为$k$步预测（$k$-step-ahead-prediction）。
由于我们的观察已经到了$x_{604}$，它的$k$步预测是${\hat{x}}_{604+k}$。
换句话说，我们必须使用我们自己的预测（而不是原始数据）来[进行多步预测]。
让我们看看效果如何。

# 初始化一个全零的张量，用于存储多步预测结果
multistep_preds = torch.zeros(T)

# 将原始数据的前 n_train + tau 个值复制到多步预测张量中
multistep_preds[: n_train + tau] = x[: n_train + tau]

# 从 n_train + tau 开始，进行多步预测
for i in range(n_train + tau, T):
    # 使用网络对前 tau 个预测值进行预测，并存储结果
    multistep_preds[i] = net(
        multistep_preds[i - tau:i].reshape((1, -1)))  # 将最近的 tau 个值重塑格式放入预测结果中，留作之后使用

# 绘制时间序列图
d2l.plot([time, time[tau:], time[n_train + tau:]],  # x轴为时间
         [x.detach().numpy(), onestep_preds.detach().numpy(),
          multistep_preds[n_train + tau:].detach().numpy()],  # y轴为原始数据、一次性预测和多步预测
         'time',  # x轴标签
         'x',  # y轴标签
         legend=['data', '1-step preds', 'multistep preds'],  # 图例
         xlim=[1, 1000],  # 设置x轴范围
         figsize=(6, 3))  # 设置图形大小为6x3英寸

如上面的例子所示，绿线的预测显然并不理想。
经过几个预测步骤之后，预测的结果很快就会衰减到一个常数。
为什么这个算法效果这么差呢？事实是由于错误的累积：
假设在步骤$1$之后，我们积累了一些错误${ϵ}_1=\overline{ϵ}$。
于是，步骤$2$的输入被扰动了${ϵ}_1$，
结果积累的误差是依照次序的${ϵ}_2=\overline{ϵ}+c{ϵ}_1$，
其中$c$为某个常数，后面的预测误差依此类推。
因此误差可能会相当快地偏离真实的观测结果。
例如，未来$24$小时的天气预报往往相当准确，
但超过这一点，精度就会迅速下降。
我们将在本章及后续章节中讨论如何改进这一点。

基于$k=1,4,16,64$，通过对整个序列预测的计算，
让我们[更仔细地看一下$k$步预测]的困难。

max_steps = 64
features = torch.zeros((T - tau - max_steps + 1, tau + max_steps))
# 列i（i<tau）是来自x的观测，其时间步从（i）到（i+T-tau-max_steps+1）
for i in range(tau):
    features[:, i] = x[i: i + T - tau - max_steps + 1]

# 列i（i>=tau）是来自（i-tau+1）步的预测，其时间步从（i）到（i+T-tau-max_steps+1）
for i in range(tau, tau + max_steps):
    features[:, i] = net(features[:, i - tau:i]).reshape(-1)
steps = (1, 4, 16, 64) #我们做了从1到64，这里只挑出这四个进行画图
d2l.plot([time[tau + i - 1: T - max_steps + i] for i in steps],
         [features[:, tau + i - 1].detach().numpy() for i in steps], 'time', 'x',
         legend=[f'{i}-step preds' for i in steps], xlim=[5, 1000],
         figsize=(6, 3))

以上例子清楚地说明了当我们试图预测更远的未来时，预测的质量是如何变化的。
虽然“$4$步预测”看起来仍然不错，但超过这个跨度的任何预测几乎都是无用的。

小结

• 内插法（在现有观测值之间进行估计）和外推法（对超出已知观测范围进行预测）在实践的难度上差别很大。因此，对于所拥有的序列数据，在训练时始终要尊重其时间顺序，即最好不要基于未来的数据进行训练。
• 序列模型的估计需要专门的统计工具，两种较流行的选择是自回归模型和隐变量自回归模型。
• 对于时间是向前推进的因果模型，正向估计通常比反向估计更容易。
• 对于直到时间步$t$的观测序列，其在时间步$t+k$的预测输出是“$k$步预测”。随着我们对预测时间$k$值的增加，会造成误差的快速累积和预测质量的极速下降。

练习

1. 改进本节实验中的模型。
   1. 是否包含了过去$4$个以上的观测结果？真实值需要是多少个？
   2. 如果没有噪音，需要多少个过去的观测结果？提示：把$\sin$和$\cos$写成微分方程。
   3. 可以在保持特征总数不变的情况下合并旧的观察结果吗？这能提高正确度吗？为什么？
   4. 改变神经网络架构并评估其性能。
2. 一位投资者想要找到一种好的证券来购买。他查看过去的回报，以决定哪一种可能是表现良好的。这一策略可能会出什么问题呢？
3. 时间是向前推进的因果模型在多大程度上适用于文本呢？
4. 举例说明什么时候可能需要隐变量自回归模型来捕捉数据的动力学模型。