13、整数、浮点数 在计算机中的存储形式

一、原码、反码、补码

---

• 关于整数的存储
  • 最高位是符号位。1 负数，0 整数，
  • 所有的数字在计算机里都是以补码的形式保存的。方便计算机的快速的计算。

1、正整数

• 正整数：源码 = 反码 = 补码 。

+11 的 32 位原码	00000000000000000000000000001011
+11 的 32 位反码	00000000000000000000000000001011
+11 的 32 位补码	00000000000000000000000000001011

2、负整数

• 负整数：
  • 源码：直接换算出来的二进制码。
  • 反码：除符号位不变之外，其它位取反。
  • 补码：
    • 负数的补码 = 反码 + 1。

-11 的 32 位原码	10000000000000000000000000001011
-11 的 32 位反码	11111111111111111111111111110100
-11 的 32 位补码	11111111111111111111111111110101

二、整数 的 存储形式

---

• 整数的存储较为简单，除第一位为符号位外，剩余所有位，存储该数的补码形式。

1、正整数

• 正整数存储：

//  4 的二进制补码是：00000000000000000000000000000100
System.out.println(" 4 的二进制补码是：" + Integer.toBinaryString(4));

2、负整数

• 负整数存储：

// -4 的二进制补码是：11111111111111111111111111111100
System.out.println("-4 的二进制补码是：" + Integer.toBinaryString(-4));

三、浮点数 IEEE 745 标准

---

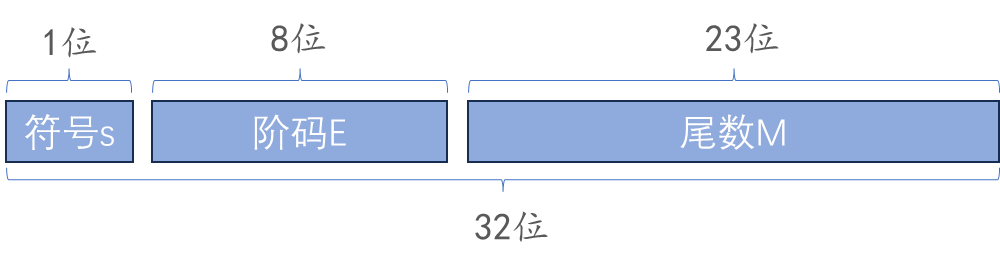
1、IEEE 754 标准下，浮点数的格式

---

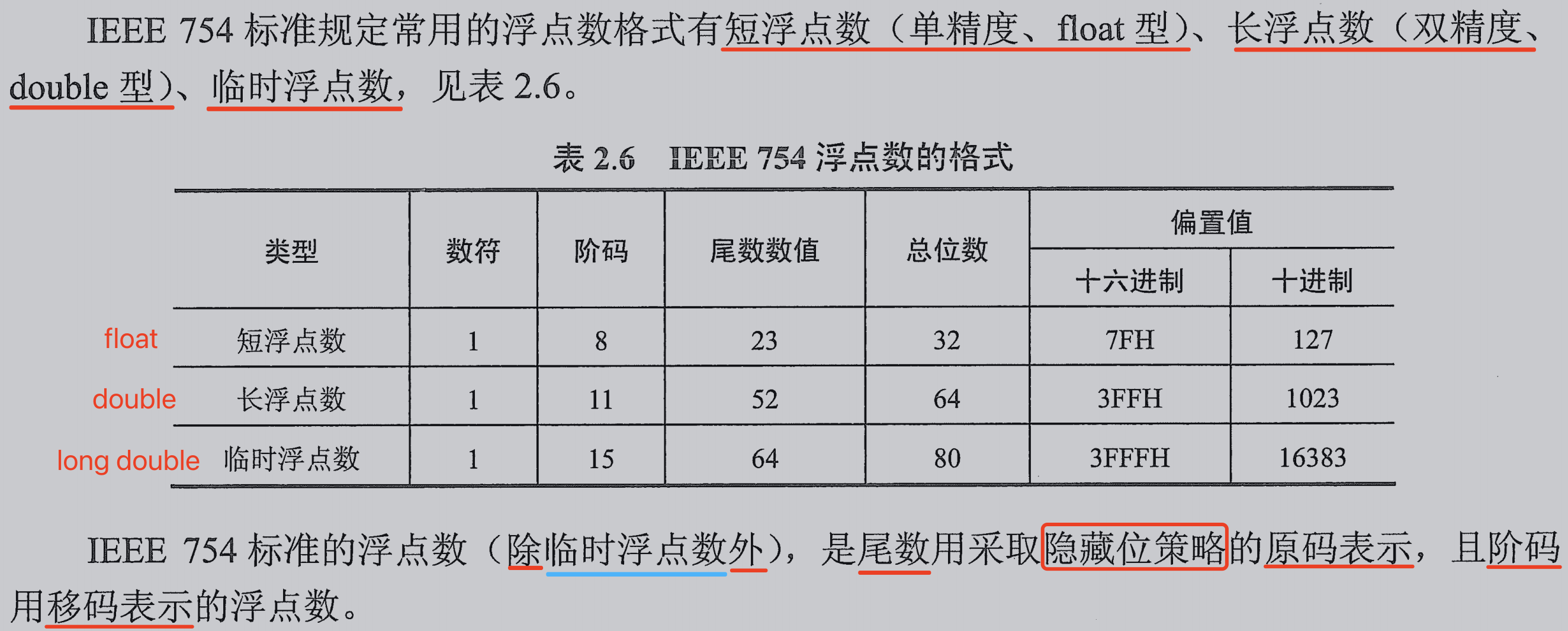
• 数符位 / 符号位（sign）：表示浮点数的正负，0 为正，1 为负。

• 指数位 / 阶码（exponent）：表示浮点数的数据大小。位数越多存储的浮点数的大小越大。
  • 为了保证阶码的存储始终为正数，用 移码 表示：
  • 移码 = 阶码真值 + 偏移量（偏置值）。
    • 单精度 - - 阶码位数是 8 ：偏移量（偏置值） = 2⁸ - 1 = 127
      
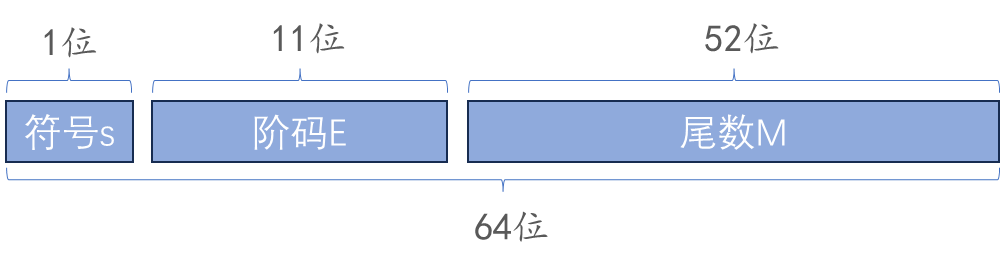
    • 双精度 – 阶码位数是 11 ：偏移量（偏置值） = 2¹¹ - 1 = 1023
      

• 尾数数值位（fraction）：表示浮点数的精度。位数越多存储的浮点数的精度越高。
  • 精度：一个数所含有效数值位的位数。用原码表示：
  • 对于规格化的二进制浮点数，数值的最高位总是 “1” 。
    • 即：将浮点数转成二进制浮点数后，将小数点左移或右移，来实现小数点前边的数为 1 **。
  • 为了使尾数多表示一位有效位，将 “1” 隐含 – 【短浮点数和长浮点数】隐含尾数最高位。

2、IEEE 754 标准下，浮点数的表示范围。

3、定点数、浮点数 表示的区别

四、37.675 作为 单精度浮点数（float）的存储计算过程

---

1、确定符号位

• 37.675 是正数，符号位为 0。

2、将十进制数转换为二进制 – 整数部分

• 十进制整数转二进制整数的方法：
  • 用十进制数除 2 取余，得到商之后继续除 2 取余，直到商为小于 1 为止。
  • 然后，将余数逆序排列。
• 将整数部分 37 转化成二进制：100101

37 ÷ 2 = 18 余 1 → 最低位		∧
18 ÷ 2 = 9  余 0						|
9 ÷ 2  = 4  余 1						|
4 ÷ 2  = 2  余 0						|
2 ÷ 2  = 1  余 0						|
1 ÷ 2  = 0  余 1 → 最高位		|                            

3、将十进制数转换为二进制 – 小数部分

• 十进制小数转成二进制小数的方法：
  • 十进制小数乘 2 ，取积中的整数部分。
  • 然后，将积中的小数部分继续乘 2 取积中的整数部分，直到积中的小数部分为 0 为止。
  • 将整数部分顺序排列。
• 将小数部分 0.675 转化成二进制：.10101100110011001100…（循环节 1100）。

0.675 × 2 = 1.35 → 取 1，剩余 0.35						|
0.35 × 2  = 0.7  → 取 0，剩余 0.7						|
0.7 × 2   = 1.4  → 取 1，剩余 0.4						|
0.4 × 2   = 0.8  → 取 0，剩余 0.8						|
0.8 × 2   = 1.6  → 取 1，剩余 0.6						|
0.6 × 2   = 1.2  → 取 1，剩余 0.2						|
0.2 × 2   = 0.4  → 取 0，剩余 0.4（开始循环）	∨

4、合并 整数 和 小数 部分 – 形成 二进制小数。

• 100101.10101100110011001100…

5、规格化 二进制小数 – 将小数点前边变成数字 1

• 将小数点左移 5 位，得到：1.0010110101100110011001100… × 2⁵ 。

6、计算 指数位

• 实际指数：5
• IEEE 754 中，单精度浮点型偏移量：127 = 2⁸ - 1
• 指数存储值：5 + 127（单精度浮点型偏移量） = 132
• 二进制指数：132 → 10000100（8 位）

7、计算 尾数位

• 规格化后的尾数：小数点后的部分，即 0010110101100110011001100
• 取前 23 位：00101101011001100110011。
  • 需检查第 24 位是否为 1 ，来决定是否进位，此处，第 24 位为 0 ，无需进位）。

8、组合各部分 – 形成（最终存储）。

• 32 位二进制表示：0 10000100 00101101011001100110011

符号位（1位）	指数位（8位）	尾数位（23位）
0	10000100	00101101011001100110011

五、根据 浮点数 的 32 位二进制表示，计算出 十进制数

• 32 位二进制表示：0 10000100 00101101011001100110011

1、确定 符号位

• 符号位：0 ，表示是个正数。

2、确定 尾数真值

• 尾数位：.00101101011001100110011 （隐含最高位 1）。
  • 因此，尾数真值 = (1.00101101011001100110011)₂ 。

3、确定 阶码真值

• 指数位（移码）：10000100 ，看做无符号数 132D 。
• 单精度浮点型偏移量：127D 。
• 阶码真值：移码 - 偏移量 = 132 - 127 = 5 。

4、确定 二进制 浮点数真值

• 浮点数真值 = (1.00101101011001100110011)₂ * 2⁵

= (100101.101011001100110011)₂

5、将二进制数转换为十进制 – 整数部分

• 整数部分为 100101₂ ，计算其十进制值：

6、将二进制数转换为十进制 – 小数部分

• 小数部分为 0.101011001100110011₂ ，计算其十进制值：

7、合并结果

• 整数部分与小数部分相加：
  • 37 + 0.674999237 ≈ 37.674999237 。