CERN ROOT 直方图

福舍

已于 2023-04-20 15:13:17 修改

阅读量2.2k

点赞数 2

文章标签： c++ 数据分析

于 2023-04-16 22:36:55 首次发布

本文链接：https://blog.youkuaiyun.com/bremss/article/details/129649218

版权

面向初学者讲解ROOT直方图基本功能

1.直方图的创建和数据导入

直方图的常用定义方法，参考ROOT:TH1 Class Reference

TH1::TH1	
(	
const char * 	name,//直方图的名字，很重要，不能重复
const char * 	title,//直方图的标题，直接体现在图像中
Int_t 	nbins,//bin的数目
Double_t 	xlow,//x轴的下限
Double_t 	xup 
)

画直方图的简单例子

TCanvas *c = new TCanvas();//创建画板

TH1 *h1 = new TH1F("h1","Gaus_10000",100,-5,5);
h1->FillRandom("gaus",10000);

h1->Draw();
c->Draw();

直方图数据的填充

几个常用的函数。

TH1::Fill	(	Double_t 	x	)	
//填入一个数据，值为x，计数为1

void TH1::FillRandom	
(	
const char * 	fname,//函数名
Int_t 	ntimes = 5000,//个数
TRandom * 	rng = nullptr//ROOT中的随机数（可以先不管） 
)
//fname可以是在ROOT中定义的基本函数，也可以是一个函数（TF1）

FillRandom的使用

TCanvas *c = new TCanvas();

TH1 *h1 = new TH1F("h1","Fill",100,-5,5);
TF1 *f  = new TF1("f","x*x");

h1->FillRandom("f",1000);

h1->Draw();
c->Draw();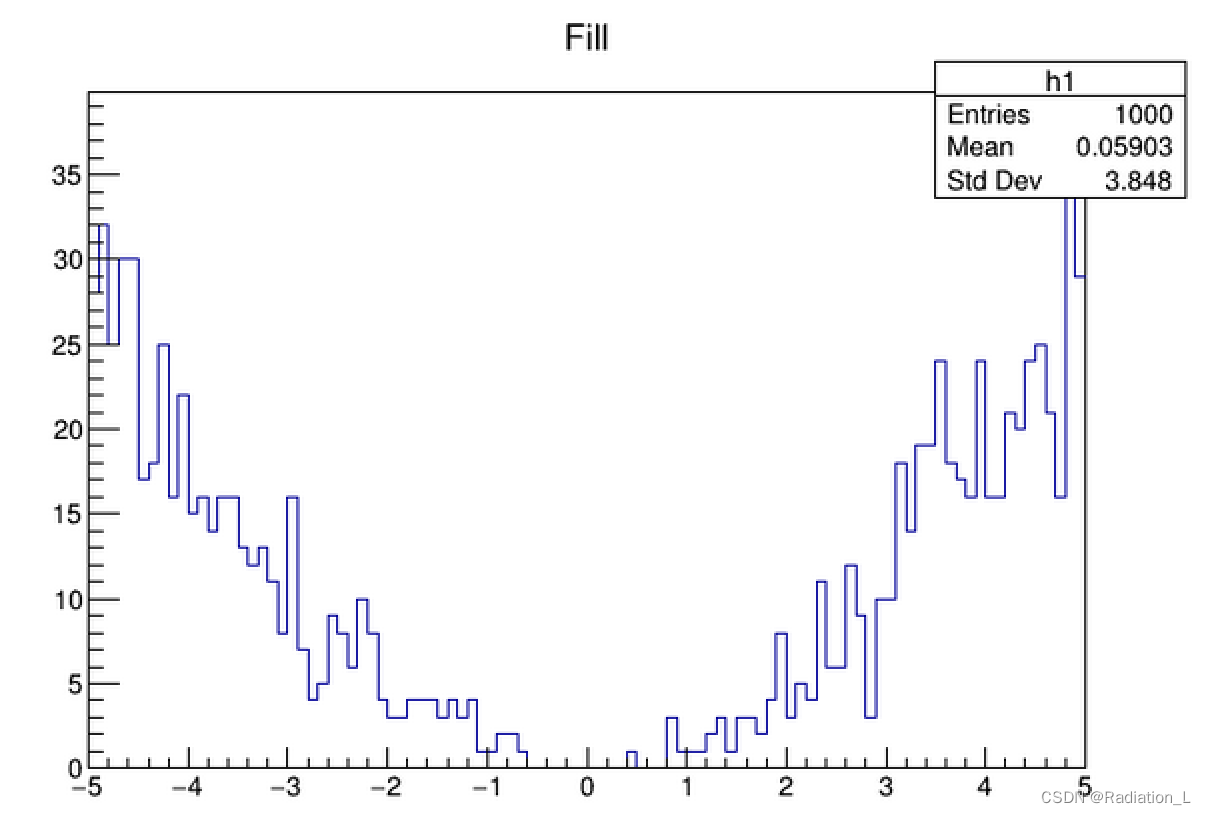

需要注意的是，在此处导入的fname首先被转化为pdf再进行抽样。也就意味着这个函数的积分必须不为0，意味着很多函数都不能进行抽样。所以需要在某函数中抽样时一般采用下面的方法——TF1::GetRandom()：

TCanvas *c = new TCanvas();

TH1 *h1 = new TH1F("h1","Fill",100,0,5);
TF1 *f = new TF1("f","2*x+5",0,5);
double x;

for (int i=0;i<10000;i++)
{
    x=f->GetRandom();
    h1->Fill(x);
}

h1->Draw();
c->Draw();

2.直方图的样式（画图）

以Gauss_10000（本篇文章第一个图）举例。

TCanvas *c = new TCanvas();

TH1 *h1 = new TH1F("h1","Gaus_10000",100,-5,5);
h1->FillRandom("gaus",10000);

h1->SetAxisRange(-2,2,"x");
h1->SetMinimum(50);

h1->SetXTitle("E");//坐标轴标题
h1->SetYTitle("N");

h1->SetLineColor(1);//线属性
h1->SetLineWidth(2);
h1->SetFillColor(23);//填充属性

h1->SetMarkerStyle(8);//Marker的样式

h1->Draw();
h1->Draw("E1 same");

c->Draw();

参考ROOT官网TH1，查看坐标轴和标题的操作，参考TAttLine，TAttFill，TAttMarker，查看颜色和数据点的样式。需要注意“same”命令的使用，可以在同一个画布上画出多张直方图。

Draw的选项参照THistPainter

图像的数据展示

使用gSytle，按照给定的选项（开关）展示直方图的数据，参考TPaveStats

gStyle->SetOptStat(mode);

mode = ksiourmen  (default = 000001111)
k = 1;  kurtosis printed
k = 2;  kurtosis and kurtosis error printed
s = 1;  skewness printed
s = 2;  skewness and skewness error printed
i = 1;  integral of bins printed
i = 2;  integral of bins with option "width" printed
o = 1;  number of overflows printed
u = 1;  number of underflows printed
r = 1;  standard deviation printed
r = 2;  standard deviation and standard deviation error printed
m = 1;  mean value printed
m = 2;  mean and mean error values printed
e = 1;  number of entries printed
n = 1;  name of histogram is printed

参考TLegend给出图例：

当不需要自定义Legend的时候，可以试试 c1->BuildLegend();

TCanvas *c1 = new TCanvas();

TH1 *h1 = new TH1F("h1","Gaus_10000",100,-5,5);
h1->FillRandom("gaus",10000);

TH1 *h2 = new TH1F("h2","Gaus_5000",100,-5,5);
h2->FillRandom("gaus",5000);

TH1 *h3 = new TH1F("h3","Gaus_10000+Gaus_5000",100,-5,5);
h3->Sumw2();
h3->Add(h1,h2,1,1);
h3->SetLineColor(6);

h1->SetLineColor(2);
h2->SetLineColor(4);

//Statistics box editing
//***************************
h3->Draw();
h1->Draw("sames");
h2->Draw("sames");
h3->Draw("sames");
c1->Update();

gStyle->SetOptStat(1110);

TPaveStats *ps = (TPaveStats*)h3->FindObject("stats");

ps->SetName("mystats");
TList *listOfLines = ps->GetListOfLines();

TLatex *myt = new TLatex(0,0,"Test = 10");
myt ->SetTextFont(42);
myt ->SetTextSize(0.03);
myt ->SetTextColor(kRed);
listOfLines->Add(myt);

//try:remove Mean
/*
TText *tconst = ps->GetLineWith("Mean");
listOfLines->Remove(tconst);
*/

h3->SetStats(0);
c1->Modified();
//***************************

auto legend = new TLegend(0.1,0.7,0.3,0.9);
legend->SetHeader("The Legend Title","C"); // option "C" allows to center the header
legend->AddEntry(h1,"Gauss 1","l");
legend->AddEntry(h2,"Gauss 2","l");
legend->AddEntry(h3,"Gauss 3","l");
legend->Draw();

c1->Draw();

！使用 %jsroot on 可以对图型做很多调整，学会利用，减少工作量

3.直方图数据获取

轴与Bin相关的数据获取，TAxis类。

查询某个Bin的上下边界（输入Bin数），查询某个数据在第几个Bin中（输入x）

//在Gauss_10000图中
TAxis * axis = h1->GetXaxis();

double n,n1,n2;

n = axis->GetNbins();

n1 = axis->GetBinLowEdge(50);//第50个Bin的左边界
n2 = axis->GetBinUpEdge(50);//第50个Bin的右边界
n3 = axis->FindBin(0.);//0所在的Bin是第几个

cout<<n1<<endl<<n2<<endl<<n3;

结果：
>>-0.1
>>0
>>51

计数和误差的数据获取，默认的误差为 $\sqrt{N}$ (由泊松分布决定)

//同样在Gauss_10000中
n1 = h1->GetBinContent(50);//得到Bin中的计数
n2 = h1->GetBinError(50);//得到Bin的误差
     
cout<<n1<<endl<<n2<<endl;

结果：
>>396
>>19.8997

4.直方图数据处理

直方图的相加和相减（Add），还可以使用THStack

直方图的相乘和相除（Multiply,Divide）

注意在归一化和加减乘除中，要正确得到统计误差，需要调用： TH1::SetDefaultSumw2()；或对每个直方图（如his）调用 his->Sumw2()；否则只会得到由计数绝对的默认误差。

TCanvas *c1 = new TCanvas();

TH1 *h1 = new TH1F("h1","Gaus_10000",100,-5,5);
h1->FillRandom("gaus",10000);

TH1 *h2 = new TH1F("h2","Gaus_1000",100,-5,5);
h2->FillRandom("gaus",1000);

h1->SetLineColor(1);
h2->SetLineColor(2);

TH1 *h3 = new TH1F("h3","h1+h2",100,-5,5);
h3->Sumw2();
h3->Add(h1,h2,1,1);
h3->SetLineColor(3);

TH1 *h4 = new TH1F("h4","h1*h2",100,-5,5); 
TH1 *h5 = new TH1F("h5","h1/h2",100,-5,5); 
h4->Sumw2();
h5->Sumw2();
h4->SetLineColor(4);
h5->SetLineColor(6);
h4->Multiply(h1,h2,1,1);
h5->Divide(h1,h2,1,1);

c1->Divide(2,2);

//original
c1->cd(1);
h1->Draw();
h2->Draw("same");

c1->cd(2);
h3->Draw();
h2->Draw("same");
h1->Draw("same");

c1->cd(3);
h4->Draw();
h2->Draw("same");
h1->Draw("same");

c1->cd(4);
h5->Draw();
h2->Draw("same");
h1->Draw("same");

c1->Draw();

直方图的归一化（normalization）

归一化到同一积分可直观比较两种分布之间的差别；可直观估计概率密度函数

TCanvas *c = new TCanvas();//创建画板

TH1 *h1 = new TH1F("h1","Gaus_10000",100,-5,5);
h1->FillRandom("gaus",10000);

h1->DrawNormalized("e", 1);

c->Draw();