毫米波雷达从入门到精通：原理、系统与相控阵天线全解析（下）

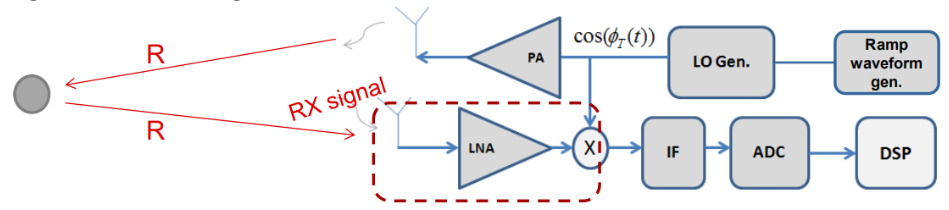
3.3 接收信号模型：目标反射与信号衰减

接收信号是发射信号经目标反射后的 “延迟版 + 衰减版 + 频移版”，需同时考虑时间延迟（对应距离）、信号衰减（对应探测范围）和多普勒频移（对应速度），三者共同构成接收信号的核心特征。

3.3.1 核心 1：时间延迟 —— 距离的 “直接映射”

延迟与距离的推导

电磁波在空气中传播速度近似为光速c=3×10^8 m/s，传播路程为 “雷达→目标→雷达” 的往返距离2R，因此：

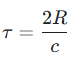
时间延迟关键参数表

参数符号	定义	单位	典型值（车载场景）	物理意义	关联公式
	信号往返时间延迟	s	0.1μs~10μs	电磁波往返目标的时间，越小表示目标越近
R	雷达与目标的直线距离	m	15m（近距）~150m（远距）	核心测量目标，决定雷达的探测范围
c	光速（电磁波传播速度）	m/s	\(3×10^8\)	恒定物理量，空气中近似等于真空中速度	-

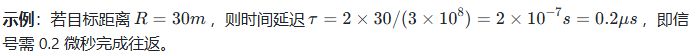
3.3.2 核心 2：信号衰减 —— 探测距离的 “天花板”

接收信号的幅度会比发射信号大幅衰减，衰减来源包括路径损耗（最主要）、目标反射损耗和雷达内部损耗，最终接收信号幅度需满足 “信噪比（SNR）≥检测阈值”，否则目标无法被识别。

雷达方程：量化衰减与接收功率

雷达方程是描述 “发射功率→接收功率” 关系的核心公式，完整表达式为：

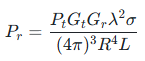
雷达方程参数拆解表

参数符号	定义	单位	典型值（车载 77GHz 雷达）	对接收功率的影响
	接收天线输出功率	W		核心输出量，需≥ADC 检测阈值（通常≥-100dBm）
	发射天线输入功率	W	0.01W（10mW，10dBm）	正相关：越大，越大，探测距离越远
	发射天线增益	无（dB 表述）	15dBi（线性值≈31.6）	正相关：增益越高，电磁波方向性越强，衰减越少
	接收天线增益	无（dB 表述）	15dBi（线性值≈31.6）	同\(G_t\)，接收端增益提升可增强信号
	毫米波波长	m	0.00389m（3.89mm）	正相关：波长越长，衰减越小（如 24GHz 比 77GHz 衰减小）
	目标雷达散射截面（RCS）	m²	汽车≈10m²，行人≈1m²，自行车≈0.5m²	正相关：目标越大，反射信号越强（如卡车 RCS 远大于摩托车）
R	雷达与目标距离	m	-	强负相关：\(R^4\)项！距离翻倍，\(P_r\)衰减 16 倍（24dB）
L	系统总损耗	无（dB 表述）	10dB（线性值≈10）	负相关：损耗包括天线损耗、电缆损耗等，需尽量降低

3.3.3 核心 3：多普勒频移 —— 速度的 “专属信号”

若雷达与目标存在径向相对运动（靠近或远离），接收信号的频率会发生偏移，这种偏移称为 “多普勒频移”，是测量目标速度的唯一依据。

多普勒频移参数表

参数符号	定义	单位	典型值（车载场景）	物理意义
	多普勒频移	Hz	-1000Hz~+1000Hz	正：目标靠近；负：目标远离；0：静止
	径向相对速度	m/s（km/h）	-30m/s（-108km/h）~+30m/s（+108km/h）	车载雷达主要测量范围（覆盖车辆行驶速度）
	毫米波波长	m	0.00389m（77GHz）	波长越短，相同速度下越大（测量越灵敏）

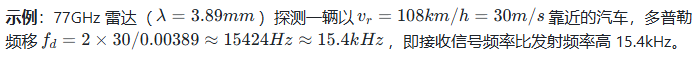
3.3.4 接收信号的完整数学模型

结合 “时间延迟 + 信号衰减 + 多普勒频移”，接收信号的时域表达式为：

接收信号与发射信号的对比表

信号类型	幅度项	频率项（载频 + 调制）	延迟项	核心差异
	1（归一化）		无	原始信号，无衰减、无延迟、无频移
	A（衰减后）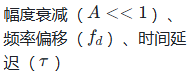

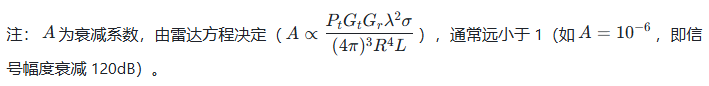
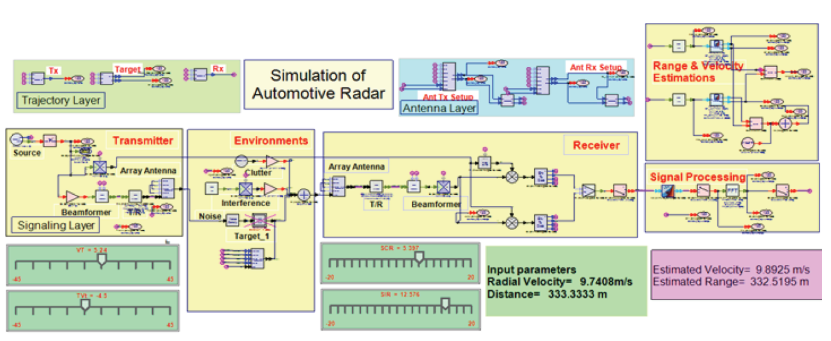
第 4 章 信号处理全流程：从模拟信号到目标信息

FMCW 雷达的核心任务是 “从接收信号中提取目标的距离、速度、角度”，这需要经过ADC 采样→1D FFT（距离）→2D FFT（速度）→CFAR 检测→角度估计→目标跟踪六大步骤，每个步骤都有明确的输入、输出和算法逻辑。

4.1 步骤 1：ADC 采样 —— 模拟信号 “数字化”

接收信号经混频器得到中频信号（IF 信号，模拟量），需通过 ADC（模数转换器）转为数字信号，才能进入后续的数字信号处理（DSP）。

ADC 采样核心参数表

参数名称	定义	单位	典型值（车载 77GHz 雷达）	对处理效果的影响
采样率\(f_s\)	每秒采样点数	Hz（SPS）	100MHz~200MHz	需满足奈奎斯特准则（\(f_s ≥ 2f_{IF,max}\)），否则信号混叠
采样位数\(N_{bit}\)	每个采样点的量化位数	bit	12bit~14bit	位数越高，量化噪声越小，SNR 越高（12bit 比 8bit SNR 高 24dB）
采样时长\(T_s\)	单 chirp 的采样时间	s	38μs（略小于\(T_c=40μs\)）	需覆盖 chirp 有效时间，避免信号截断
单 chirp 采样点数\(N_{1D}\)	单 chirp 的采样总数	点	256 点～512 点	决定 1D FFT 的点数，点数越多，距离分辨率越高
量化范围	ADC 可处理的电压范围	V	-1V~+1V（峰峰值 2V）	需匹配中频信号幅度，避免过载（削波）或欠量程

4.2 步骤 2：1D FFT（距离 FFT）—— 提取目标距离

1D FFT 的核心是 “将时域的中频信号转换为频域的距离谱”，利用 “中频频率f_IF与目标距离R的线性关系”，直接从频域峰值位置读取目标距离。

4.2.1 中频频率与距离的关系推导

混频器的作用是 “将发射信号与接收信号相乘，滤除高频分量后得到中频信号”，其输出的中频频率fIF由两部分组成：

4.2.2 1D FFT 核心参数与性能表

参数名称	定义	单位	典型值（车载场景）	计算逻辑 / 物理意义
1D FFT 点数\(N_{1D}\)	FFT 运算的输入点数	点	256 点 / 512 点	通常取 2 的整数次幂（如 256=2^8），便于 FFT 硬件加速
距离分辨率\(\delta R\)	能区分的最小距离差	m	0.075m（7.5cm）	\(\delta R = \frac{c}{2B}\)，带宽\(B\)越大，分辨率越高
最大探测距离\(R_{max}\)	能检测的最远距离	m	150m	\(R_{max} = \frac{c \cdot f_{IF,max}}{2S}\)，\(f_{IF,max}\)为最大中频频率（由 ADC 采样率限制）
距离谱峰值位置\(k_R\)	距离谱中峰值对应的频率点	点	第 50 点（示例）	目标距离\(R = k_R \cdot \delta R\)（忽略窗函数影响）
窗函数类型	降低 FFT 频谱泄漏的函数	-	汉宁窗 / 布莱克曼窗	矩形窗频谱泄漏严重，汉宁窗可改善，但会降低分辨率

4.2.3 1D FFT 的 “频谱泄漏” 问题与解决

当目标距离对应的中频频率\(f_{IF}\)不恰好落在 FFT 的频率点上时，会导致 “频谱泄漏”—— 峰值能量分散到多个频率点，降低距离测量精度。解决方法是加窗函数，不同窗函数的性能对比如下：

窗函数类型	主瓣宽度（相对矩形窗）	旁瓣衰减（dB）	分辨率损失	适用场景
矩形窗	1（最窄）	-13	无	对分辨率要求极高、目标少的场景（如实验室测距）
汉宁窗	2	-31	约 50%	平衡分辨率与旁瓣的通用场景（如车载近距检测）
汉明窗	2	-41	约 50%	旁瓣要求稍高的场景
布莱克曼窗	3	-57	约 100%	多目标、强杂波场景（如城市道路 ADAS）

4.3 步骤 3：2D FFT（多普勒 FFT）—— 提取目标速度

1D FFT 仅能得到目标距离，但无法区分 “静止目标” 和 “运动目标”（因两者都可能在同一距离点产生峰值）。2D FFT 通过 “对多帧 chirp 的距离谱进行 FFT”，提取多普勒频移\(f_d\)，进而得到目标速度。

4.3.1 2D FFT 的输入与输出逻辑

4.3.2 2D FFT 核心参数与性能表

参数名称	定义	单位	典型值（车载场景）	计算逻辑 / 物理意义
2D FFT 点数\(N_{2D}\)	一帧内的 chirp 数量	个	128 点 / 256 点	通常取 2 的整数次幂，点数越多，速度分辨率越高
速度分辨率\(\delta v\)	能区分的最小速度差	m/s	0.1m/s	\(\delta v = \frac{\lambda}{2 T_{frame}}\)，\(T_{frame}=N_{2D}×T_c\)（帧周期）
最大测速范围\(v_{max}\)	能检测的最大速度	m/s（km/h）	±30m/s（±108km/h）	\(v_{max} = \frac{\lambda f_{PRF}}{4}\)，\(f_{PRF}=1/T_c\)（chirp 重复频率）
多普勒谱峰值位置\(k_v\)	多普勒谱中峰值对应的频率点	点	第 64 点（示例）	目标速度\(v_r = (k_v - N_{2D}/2) \cdot \delta v\)（负号对应远离）
帧周期\(T_{frame}\)	一帧 chirp 的总时长	s	10.24ms（256×40μs）	决定雷达更新率（更新率 = 1/\(T_{frame}\)≈97.7Hz）

4.3.3 速度模糊与解决方法

当目标速度\(|v_r|>v_{max}\)时，多普勒频移\(|f_d|>f_{PRF}/2\)（奈奎斯特频率），导致 2D FFT 无法正确识别频移方向，出现 “速度模糊”（如将 + 30m/s 识别为 - 18.6m/s）。解决方法是参差 PRF（多组不同\(T_c\)的 chirp） ，通过多组测量结果解模糊。

解决方法	原理	优点	缺点	适用场景
参差 PRF	发射 2~3 组不同\(T_c\)的 chirp，利用多组\(v_r\)的模糊结果反推真实速度	无需增加硬件，软件即可实现	增加帧周期（降低更新率）	车载高速场景（如高速 ADAS）
增加\(N_{2D}\)	增加一帧 chirp 数量，降低\(\delta v\)，扩大\(v_{max}\)	实现简单，无额外延迟	增加算力和帧周期	低速场景（如泊车辅助）
双频段雷达	用两个不同频段（如 77GHz+24GHz）测量，利用波长差异解模糊	无速度模糊，精度高	硬件复杂度高，成本高	高端自动驾驶（L4+）

4.4 步骤 4：CFAR 检测 —— 从 “噪声” 中识别 “目标”

“距离 - 多普勒” 二维谱中，除了目标信号的峰值，还有大量背景噪声（如热噪声、地面杂波），CFAR（Constant False Alarm Rate，恒虚警率）检测的核心是 “自适应设定阈值”，在保证 “误检率（虚警）恒定” 的前提下，将目标峰值从噪声中分离出来。

4.4.1 CFAR 的核心逻辑

1. 选取参考窗：以当前检测点为中心，设置 “保护窗”（避免目标能量影响参考）和 “背景窗”（统计噪声能量）；

1. 计算噪声功率：对背景窗内的信号幅度取平均，得到噪声功率估计值；

1. 设定检测阈值：阈值 = 噪声功率 × 阈值系数（由目标检测率和虚警率要求决定）；

1. 判决目标：若当前检测点的幅度 > 阈值，则判定为 “目标”；否则为 “噪声”。

4.4.2 主流 CFAR 算法对比表

CFAR 算法类型	参考窗形状	噪声功率计算方式	优点	缺点	适用场景
CA-CFAR（单元平均）	对称矩形（左右 / 上下）	所有背景窗点的平均值	计算简单，噪声均匀时性能好	多目标时 “遮蔽效应”（强目标掩盖弱目标）	空旷场景（如高速路）
GO-CFAR（选大）	对称矩形（左右分窗）	左右两个子背景窗的最大值	抗杂波能力强（如地面强反射）	虚警率略高，多目标遮蔽效应仍存在	城市道路（多杂波）
SO-CFAR（选小）	对称矩形（左右分窗）	左右两个子背景窗的最小值	虚警率低，适合低噪声场景	抗杂波能力弱，易漏检	郊区场景（低杂波）
OS-CFAR（排序）	圆形 / 矩形	背景窗点排序后取第 k 个值（如中值）	抗异常值（如孤立强杂波）能力强	计算复杂度高，实时性差	复杂环境（如停车场）

4.4.3 CFAR 关键参数表

参数名称	定义	单位	典型值（车载场景）	对检测性能的影响
保护窗大小\(N_g\)	中心检测点周围的保护点数	点	2~4 点	过小：目标能量进入背景窗，阈值偏高（漏检）；过大：背景窗变小，噪声估计不准
背景窗大小\(N_b\)	用于统计噪声的点数	点	8~16 点	过小：噪声估计波动大；过大：多目标遮蔽效应严重
阈值系数\(α\)	阈值与噪声功率的比值	无（dB 表述）	10dB~15dB	过小：虚警率高（误判噪声为目标）；过大：漏检率高（漏判弱目标）
虚警率\(P_{fa}\)	噪声被误判为目标的概率	%	10^{-6}~10^{-4}（0.0001%~0.01%）	车载场景需极低虚警率，避免频繁误触发 AEB
检测率\(P_d\)	目标被正确检测的概率	%	≥99%	确保关键目标（如行人、车辆）不被漏检

示例：CA-CFAR 在车载场景的应用：

• 保护窗\(N_g=2\)点，背景窗\(N_b=16\)点（左右各 8 点）；

• 若背景窗内信号幅度平均值为 10（归一化），阈值系数\(α=10dB\)（线性值≈10），则阈值 = 10×10=100；

• 若当前检测点幅度为 120>100，则判定为目标；若幅度为 80<100，则判定为噪声。

4.5 步骤 5：角度估计 —— 确定目标的 “方位”

通过 1D/2D FFT，雷达已能获取目标的 “距离 - 速度” 信息，但还需知道目标的 “角度”（水平角\(θ\)、垂直角\(φ\)），才能实现 “3D 定位”。角度估计的核心是利用接收天线阵列的相位差，通过波束赋形或超分辨算法计算目标角度。

4.5.1 天线阵列与相位差的关系

4.5.2 主流角度估计算法对比表

算法类型	核心原理	角度分辨率	计算复杂度	硬件要求	适用场景
波束赋形（BF）	对各天线信号加权求和，形成指向性波束，峰值方向为目标角度	低（\(10°~30°\)）	低（仅需加权求和）	普通天线阵列	低成本场景（如 24GHz 倒车雷达）
MUSIC 算法	基于信号子空间与噪声子空间正交性，通过谱峰搜索得到角度	高（\(1°~5°\)）	高（需矩阵分解、谱峰搜索）	多天线阵列（≥4 单元）	中高端车载（如 77GHz 前向雷达）
ESPRIT 算法	利用阵列平移不变性，无需谱峰搜索，直接计算角度	高（\(1°~5°\)）	中（矩阵分解，无搜索）	多天线阵列（≥4 单元）	实时性要求高的场景（如 ADAS）
3D FFT	对 “距离 - 多普勒 - 天线” 三维数据做 FFT，直接得到角度	中（\(5°~10°\)）	中（FFT 硬件加速）	规则天线阵列（如 4×4 面阵）	3D 雷达（如激光雷达融合场景）

4.5.3 角度估计关键参数表

参数名称	定义	单位	典型值（车载场景）	对角度性能的影响
天线单元数\(M\)	接收天线阵列的单元数量	个	4~16 个	单元越多，角度分辨率越高（MUSIC 算法分辨率≈\(λ/(M d)\)）
单元间距\(d\)	相邻天线单元的距离	m	\(λ/2\)（≈1.94mm，77GHz）	\(d>λ/2\)会出现栅瓣（虚假角度），\(d<λ/2\)会降低增益
角度分辨率\(\deltaθ\)	能区分的最小角度差	°	1°~5°（前向雷达）	分辨率越高，越能区分相邻目标（如并排行驶的两辆车）
角度测量范围\(θ_{range}\)	能检测的角度范围	°	±60°（前向雷达）、±90°（侧后雷达）	范围越大，覆盖视野越广（如侧后雷达需覆盖车辆两侧）
角度误差\(\Deltaθ\)	测量角度与真实角度的偏差	°	≤1°（静态）、≤3°（动态）	误差越小，目标定位越准（如 AEB 的制动距离计算）

4.6 步骤 6：目标跟踪 —— 稳定输出目标信息

通过 CFAR 检测和角度估计，雷达会得到 “离散的目标点”（每帧一个点），但目标是连续运动的，需通过目标跟踪算法将多帧的目标点关联起来，输出 “连续、平滑的目标轨迹”，避免因噪声导致的 “目标跳变” 或 “目标丢失”。

4.6.1 目标跟踪的核心逻辑

1. 数据关联：将当前帧检测到的目标点与上一帧的跟踪目标进行匹配（如用 “匈牙利算法”“最近邻算法”）；

1. 状态估计：对匹配成功的目标，用滤波算法（如卡尔曼滤波）估计其当前状态（距离、速度、加速度、角度）；

1. 目标管理：对未匹配的检测点，判定为 “新目标” 并初始化跟踪；对未匹配的跟踪目标，判定为 “暂存” 或 “消失”（如连续 3 帧未匹配则删除）。

4.6.2 主流目标跟踪算法对比表

算法类型	核心原理	跟踪精度	计算复杂度	多目标处理能力	适用场景
卡尔曼滤波（KF）	线性系统下的最优状态估计，假设噪声为高斯分布	中（线性运动）	低（矩阵乘法）	弱（易混淆）	匀速运动场景（如高速路车辆）
扩展卡尔曼滤波（EKF）	对非线性系统做一阶泰勒展开，近似线性化	中（非线性运动）	中（雅克比矩阵）	弱	低速、变加速场景（如城市道路）
无迹卡尔曼滤波（UKF）	用 “sigma 点” 近似非线性分布，无需线性化	高（非线性运动）	高（sigma 点计算）	中	复杂运动场景（如行人横穿马路）
粒子滤波（PF）	用大量粒子近似概率分布，无噪声分布假设	高（任意运动）	极高（粒子数量多）	强	极端复杂场景（如多目标交叉）
联合概率数据关联（JPDA）	对多目标 - 多量测的所有可能关联计算概率，选择最优	高（多目标）	高（概率计算）	强	密集多目标场景（如拥堵路段）

4.6.3 目标跟踪关键参数表

参数名称	定义	单位	典型值（车载场景）	对跟踪性能的影响
跟踪更新率	每秒输出跟踪结果的次数	Hz	50Hz~100Hz	更新率越高，对快速运动目标的跟踪越及时（如行人突然横穿）
新目标确认帧数	判定为 “稳定目标” 所需的连续匹配帧数	帧	2~3 帧	过少：易将噪声误判为目标；过多：新目标确认延迟长
目标消失帧数	判定为 “目标消失” 所需的连续未匹配帧数	帧	3~5 帧	过少：易丢失短暂被遮挡的目标；过多：残留无效目标
滤波增益\(K\)	卡尔曼滤波中调整估计值与量测值权重的参数	无	0.1~0.5	过大：跟踪灵敏但易受噪声干扰；过小：跟踪平滑但延迟大
多目标容量	同时跟踪的最大目标数量	个	32~128 个	容量越大，越能应对复杂交通场景（如拥堵路段）

第 5 章 相控阵毫米波天线：雷达的 “眼睛”

天线是毫米波雷达 “发射和接收电磁波” 的核心部件，而相控阵天线通过 “控制各单元的相位” 实现 “无机械转动的波束扫描”，大幅提升雷达的灵活性和响应速度，是中高端毫米波雷达的标配。

5.1 相控阵天线的核心优势：为什么替代机械扫描？

传统机械扫描天线通过 “电机转动天线” 改变波束方向，而相控阵天线通过 “电子相位控制” 实现波束扫描，两者差异显著：

对比维度	机械扫描天线	相控阵天线	核心优势（相控阵）
扫描方式	电机转动天线单元	电子控制各单元相位	无机械磨损，寿命长（>10 年 vs 机械 < 5 年）
扫描速度	慢（<100°/s）	快（>1000°/s）	快速覆盖全视野（如 100ms 完成 ±60° 扫描）
扫描灵活性	仅能一维扫描（如水平）	二维 / 三维扫描（水平 + 垂直）	实现 3D 定位（如区分地面目标和空中目标）
多目标能力	一次仅能跟踪 1 个目标	同时跟踪多目标（波束赋形）	应对复杂场景（如多车并行、行人横穿）
体积与功耗	体积大（含电机）、功耗高	体积小（集成化）、功耗低	适合车载小型化需求（如前向雷达体积 < 100cm³）
可靠性	机械故障风险高（电机卡滞）	全电子结构，可靠性高	车载场景故障率 < 0.1%/ 年

5.2 相控阵天线的工作原理：相位控制与波束扫描

相控阵天线由N 个天线单元、N 个移相器和1 个波束控制器组成，核心是 “通过移相器调整各单元的相位，使电磁波在特定方向叠加增强，形成波束”。

5.2.1 相位控制的数学原理

假设相控阵为均匀线性阵列（ULA），有\(N\)个天线单元，单元间距\(d=λ/2\)，目标角度为\(θ_0\)，则：

1. 波束控制器向第\(k\)个移相器发送 “相位指令”\(\phi_k = \frac{2\pi d k \sin\theta_0}{\lambda}\)（\(k=0,1,...,N-1\)）；

1. 第\(k\)个天线单元的发射信号相位为\(\phi_k\)，相邻单元的相位差为\(\Delta\phi = \frac{2\pi d \sin\theta_0}{\lambda}\)；

1. 所有单元的电磁波在\(\theta_0\)方向 “同相位叠加”，形成波束峰值；在其他方向 “反相位抵消”，信号减弱。

5.2.2 波束扫描的实现过程

当需要将波束从\(\theta_0\)转向\(\theta_1\)时，仅需调整移相器的相位指令：

• 新相位指令\(\phi_k' = \frac{2\pi d k \sin\theta_1}{\lambda}\)；

• 相邻单元的相位差变为\(\Delta\phi' = \frac{2\pi d \sin\theta_1}{\lambda}\)；

• 电磁波在\(\theta_1\)方向叠加增强，波束完成转向，整个过程无需任何机械运动，耗时仅数微秒。

5.3 相控阵天线的关键性能指标

相控阵天线的性能直接决定雷达的 “视野范围”“探测距离” 和 “角度分辨率”，核心指标如下：

指标名称	定义	单位	典型值（车载 77GHz 相控阵）	对雷达性能的影响
阵列规模	天线单元的总数（行数 × 列数）	个	16 单元（4×4 面阵）~64 单元（8×8 面阵）	单元越多，波束增益越高、角度分辨率越高
波束增益\(G\)	天线将功率集中到波束方向的能力	dBi	18dBi~25dBi	增益越高，探测距离越远（\(R_{max} \propto \sqrt{G}\)）
波束宽度（3dB）	波束峰值下降 3dB 的角度范围	°	水平：3°~5°，垂直：5°~10°	宽度越窄，角度分辨率越高（如 3° 可区分 30m 处相距 1.6m 的两辆车）
扫描范围	波束能覆盖的角度范围	°	水平：±60°，垂直：±15°	范围越大，雷达视野越广（如 ±60° 可覆盖前向 3 车道）
栅瓣抑制	抑制除主瓣外的虚假波束（栅瓣）的能力	dB	≤-30dB	栅瓣过大会导致 “虚假目标”（如将左侧目标误判为右侧）
旁瓣抑制	抑制主瓣周围旁瓣的能力	dB	≤-25dB	旁瓣过大会导致 “弱目标漏检”（旁瓣噪声掩盖弱目标）
相位精度	移相器实际相位与指令相位的偏差	°	≤5°	相位误差越大，波束指向精度越低、增益损失越大
带宽	天线能有效工作的频率范围	GHz	4GHz（76~80GHz）	带宽需覆盖雷达射频带宽（如 2GHz），否则信号衰减大

示例：4×4 面阵（16 单元）77GHz 相控阵天线：

• 波束增益\(G=20dBi\)（线性值 = 100），相比单单元天线（\(G=5dBi\)），探测距离提升\(\sqrt{100/3.16}≈5.6\)倍；

• 水平波束宽度 = 3°，在 30m 距离处，波束覆盖的水平宽度 = 2×30×tan (3°/2)≈1.57m，可精准定位单车道内的目标；

• 扫描范围 ±60°，在 100m 距离处，波束覆盖的水平范围 = 2×100×tan (60°)≈346m，可覆盖前向多车道。

5.4 相控阵天线的类型：按结构与功能划分

根据阵列结构、馈电方式和功能，相控阵天线可分为多种类型，车载毫米波雷达常用以下 3 类：

5.4.1 按阵列结构划分

类型名称	结构特点	优点	缺点	适用场景
均匀线性阵列（ULA）	单元沿一条直线均匀排列	结构简单，仅需一维相位控制	仅能一维扫描（如水平），无垂直角度分辨	低成本侧后雷达（如 BSD 盲区监测）
均匀面阵（URA）	单元沿 x、y 轴均匀排列（如 4×4）	二维扫描（水平 + 垂直），可 3D 定位	结构复杂，单元数量多，成本高	中高端前向雷达（如 AEB）
稀疏阵列	单元非均匀排列（如随机分布）	减少单元数量，降低成本	旁瓣较高，需复杂算法抑制	平衡成本与性能的场景（如 L2+ ADAS）

5.4.2 按馈电方式划分

类型名称	馈电特点	优点	缺点	适用场景
有源相控阵（AESA）	每个单元配独立的 T/R（发射 / 接收）模块	波束灵活（可同时形成多波束），损耗低	成本高（T/R 模块贵），功耗高	高端自动驾驶（L4+）
无源相控阵（PESA）	所有单元共享一个发射机 / 接收机，通过移相器馈电	成本低，结构简单	波束灵活度低（仅单波束），损耗高	中端 ADAS（L2）

5.4.3 车载雷达常用相控阵类型对比

类型	阵列结构	馈电方式	单元数量	成本	核心应用
侧后雷达专用	ULA（8 单元）	PESA	8	低	BSD（盲区监测）、LCA（变道辅助）
前向中距雷达	URA（16 单元）	PESA	16	中	ACC（自适应巡航）、AEB（紧急制动）
前向远距雷达	URA（64 单元）	AESA	64	高	L4 自动驾驶、远距离目标检测（>200m）

5.5 相控阵天线的设计挑战与解决方案

毫米波频段（尤其是 77GHz）的天线设计面临 “波长极短（≈4mm）、损耗大、集成化难” 等挑战，需针对性解决：

设计挑战	具体问题	解决方案	效果验证
单元间距与栅瓣	单元间距\(d>λ/2\)时，易出现栅瓣（虚假波束）	1. 严格控制\(d=λ/2\)；2. 采用稀疏阵列；3. 相位加权抑制	栅瓣抑制≤-30dB，无虚假目标
高频损耗	77GHz 信号在电缆、接头处衰减大（每米衰减 > 10dB）	1. 采用微带天线（集成在 PCB 上，无电缆）；2. 缩短信号路径；3. 用低损耗介质（如罗杰斯 4350）	总损耗降低至 < 5dB，增益提升 3~5dBi
集成化难度	多单元天线 + 移相器 + T/R 模块体积大，难以车载安装	1. 采用 MMIC（单片微波集成电路），将天线与芯片集成；2. 多层 PCB 设计，堆叠电路	天线 + 芯片体积 < 50cm³，适合车载前向安装
散热问题	AESA 的 T/R 模块工作时发热量大（每模块 > 1W）	1. 采用高导热材料（如铝基板）；2. 设计散热鳍片；3. 优化电源管理，降低功耗	工作温度控制在 - 40℃~85℃（车载温度范围）
相位误差	移相器、电缆的相位偏差导致波束指向不准	1. 采用高精度移相器（相位精度≤5°）；2. 实时相位校准（如用校准天线）；3. 软件补偿算法	波束指向误差≤1°，角度测量精度高

案例：某车载 77GHz AESA 天线的设计方案：

• 阵列结构：8×8 URA（64 单元），单元间距\(d=λ/2=1.94mm\)；

• 馈电方式：每个单元配独立 T/R 模块（MMIC 集成）；

• 散热设计：铝基板 + 散热鳍片，功耗控制在 15W 以内；

• 相位校准：内置校准天线，每帧自动校准相位误差；

• 性能指标：增益 25dBi，波束宽度 3°，扫描范围 ±60°，栅瓣抑制 - 35dB，满足 L4 自动驾驶需求。