各相关系数

肯德尔系数（Kendall’s tau）

适用于有序数据，可以用来评估两个有序变量之间的单调关系。

适用情形：

• 数据是非正态分布的，或者包含极端值时。
• 数据是有序数据，例如排名。

局限性：

• 仅能衡量两个变量之间的顺序关系，不能直接反映线性相关性。
• 对于大样本计算可能比较耗时。

import numpy as np
from scipy.stats import kendalltau

# 示例数据
x = [1, 2, 3, 4]
y = [3, 2, 1, 4]

# 计算肯德尔系数和 p 值
tau, p_value = kendalltau(x, y)

print(f"肯德尔系数 (tau): {tau}")
print(f"p 值: {p_value}")

公式参考：https://docs.scipy.org/doc/scipy-0.19.1/reference/generated/scipy.stats.kendalltau.html

皮尔逊相关系数

用于度量线性关系，要求数据是连续且服从正态分布。【上学教的最普通的那种】

import numpy as np
from scipy.stats import pearsonr
# 示例数据

x = [2, 3, 4, 5, 6]
y = [5, 6, 7, 8, 9]
# 计算皮尔逊相关系数

pearson_corr, p_value = pearsonr(x, y)
print(f"皮尔逊相关系数: {pearson_corr}, p 值: {p_value}")

注意：

离群值可能显著影响 Pearson 系数的计算结果

Spearman相关系数

基于排序的相关系数，不依赖于数据的具体分布，对异常值也不敏感。
d为秩之差

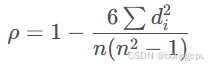
import numpy as np
from scipy.stats import spearmanr

# 示例数据
x = [10, 12, 14, 16, 18]
y = [7, 9, 11, 13, 15]

# 计算 Spearman 相关系数
spearman_corr, p_value = spearmanr(x, y)
print(f"Spearman 相关系数: {spearman_corr}, p 值: {p_value}")