机器学习入门(一): 机器学习入门和线性回归

于 2023-02-20 16:14:02 发布
阅读量391 收藏 2
点赞数 3
CC 4.0 BY-SA版权
分类专栏： 机器学习笔记 文章标签： 机器学习 线性回归 逻辑回归
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/bobchen1017/article/details/129123926
本文介绍了线性模型，包括线性回归、逻辑回归和softmax，以及有监督和无监督学习的基本概念。详细讲解了线性回归的最小二乘法推导和梯度下降法，包括批量、随机和小批量梯度下降的特点与优缺点。同时，讨论了数据预处理中的归一化对模型训练速度的影响，以及正则化在防止过拟合中的作用，如L1和L2正则化。最后提到了多项式回归作为优化策略之一。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

1. 线性模型

  • 线性回归，逻辑回归，softmax都是属于线性模型，通过线性的前向传播和反向传播所得到的权重来对数据进行分类和回归。

2. 及其学习简单的回归术语及数学

2.1 有监督学习: 有标签和数据

  1. 分类：标签是离散值(带类别的)
  2. 回归: 标签是连续值

2.2 无监督学习

  • 没有标签的学习

2.3 术语: 真实值，预测值，误差，最优解，整体误差

  1. Actual Value: 真实值，一般使用y表示
  2. predicted value: 预测值，通过去数据和权重得到的结果
  3. Error: 误差，预测值和真实值的差距，一般用e表示
  4. Loss: 整体的误差通过损失函数计算得到，损失函数有很多种

2.4 矩阵的转置以及求导

在这里插入图片描述

2.5 模型的判断效果(Loss)

  1. MSE: 误差平方和, 趋近于0表示模型越拟合训练数据
  2. RNSE: MSE的平方根，作用同MSE
  3. R^2 取值范围(负无穷,1],值越大表示模型越拟合，最优解是1, 当模型预测为随机值的时候，有可能是负的，若预测值恒为样本期望，R^2 为0
  4. TSS： total Sum of Square,表示样本之间的差异情况，是伪方差的m倍 Sum[(y - y_mean)**2]
  5. RSS：残差平方和RSS，统计学上把数据点与它在回归直线上相应位置的差异称为残差，把每个残差平方之后加起来 称为残差平方和（相当于实际值与预测值之间差的平方之和）。它表示随机误差的效应。一组数据的残差平方和越小,其拟合程度越好。

3. 线性回归公式推导(最小二乘法)

3.1 最小二乘法不用训练直接就可以拿来做任务

在这里插入图片描述

3.2 误差的概念

在这里插入图片描述

3.3 误差是正态分布的，x 是误差，通过截距项把u = 0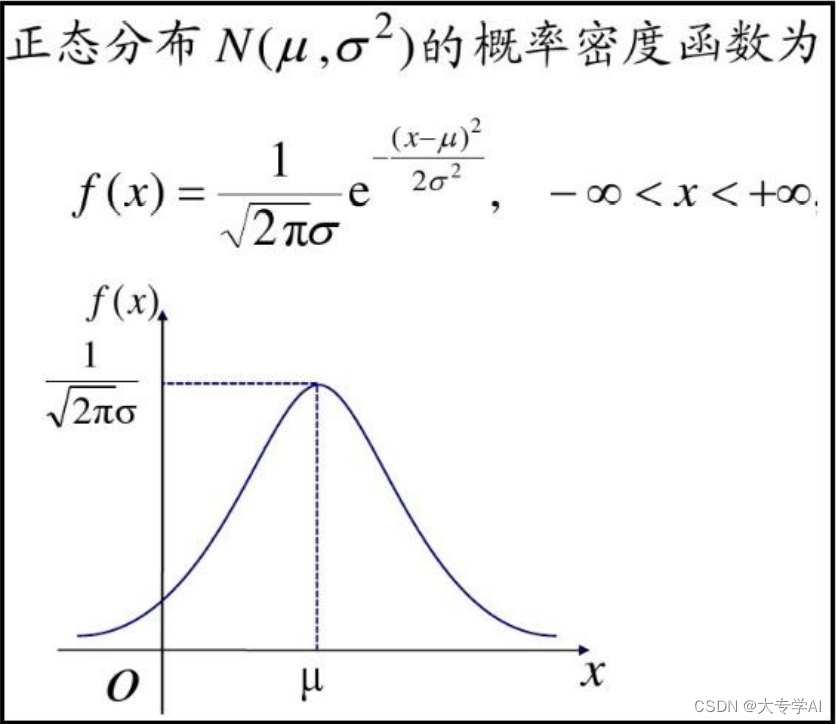在这里插入图片描述

3.4 最小二乘法推导

  • 引入似然函数把累乘转换成累加问题，减少计算量，得到最终关注的函数
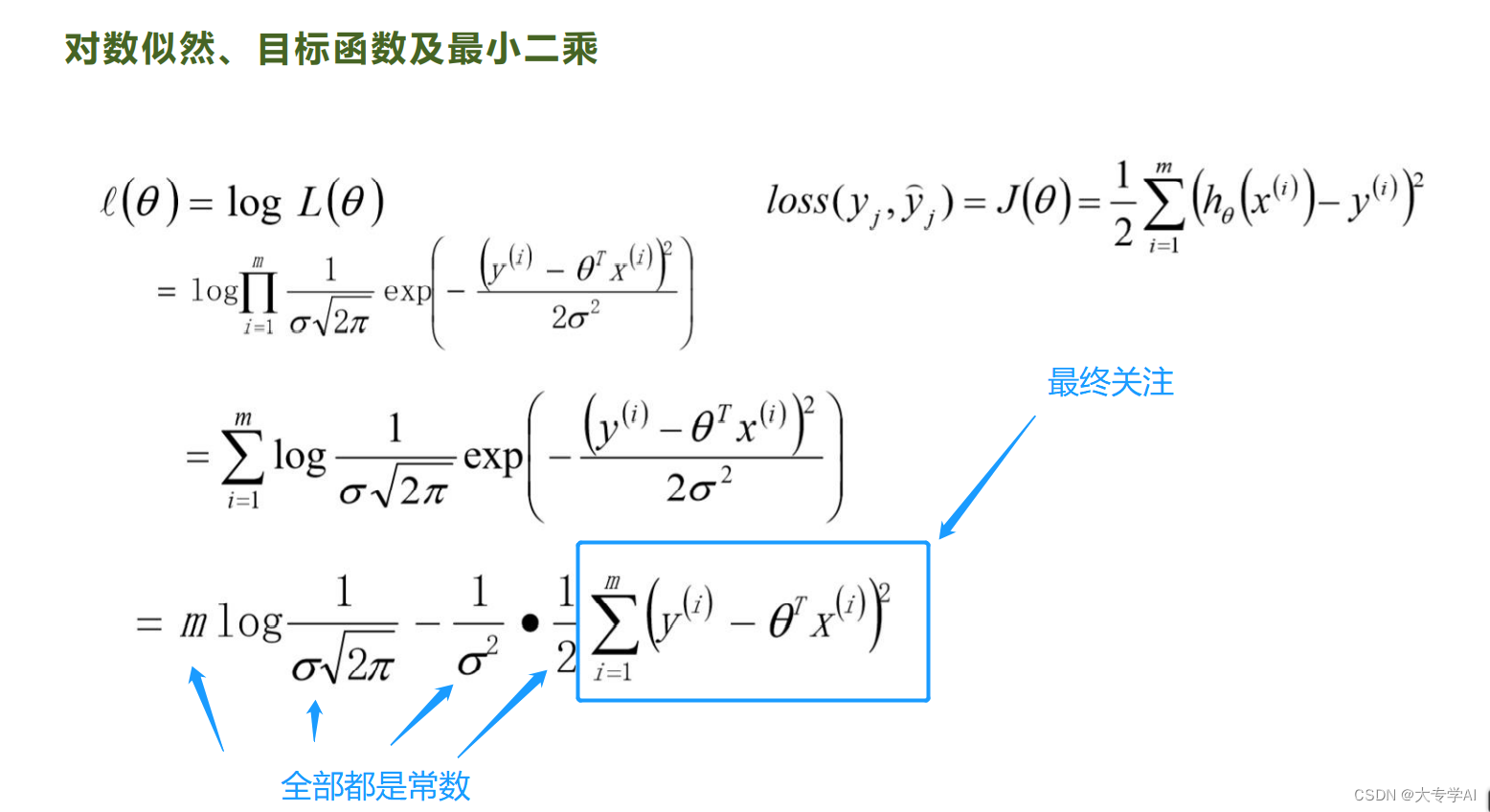
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

3.5 sklearn实现最小二乘法

在这里插入图片描述

3.6 最小二乘法的局限性

  1. 最小二乘法需要对矩阵求逆矩阵
  2. 如果数据量一大，对于计算会很痛苦，因为每一次推理都会涉及大量的矩阵计算，通过训练出一个theta就会很省事
  3. 这就是梯度下降法

4. 梯度下降法(理论)

4.1 梯度下降法

在这里插入图片描述

4.2 目标损失函数(LOSS)

在这里插入图片描述

4.3 梯度下降的公式

使用平方损失函数
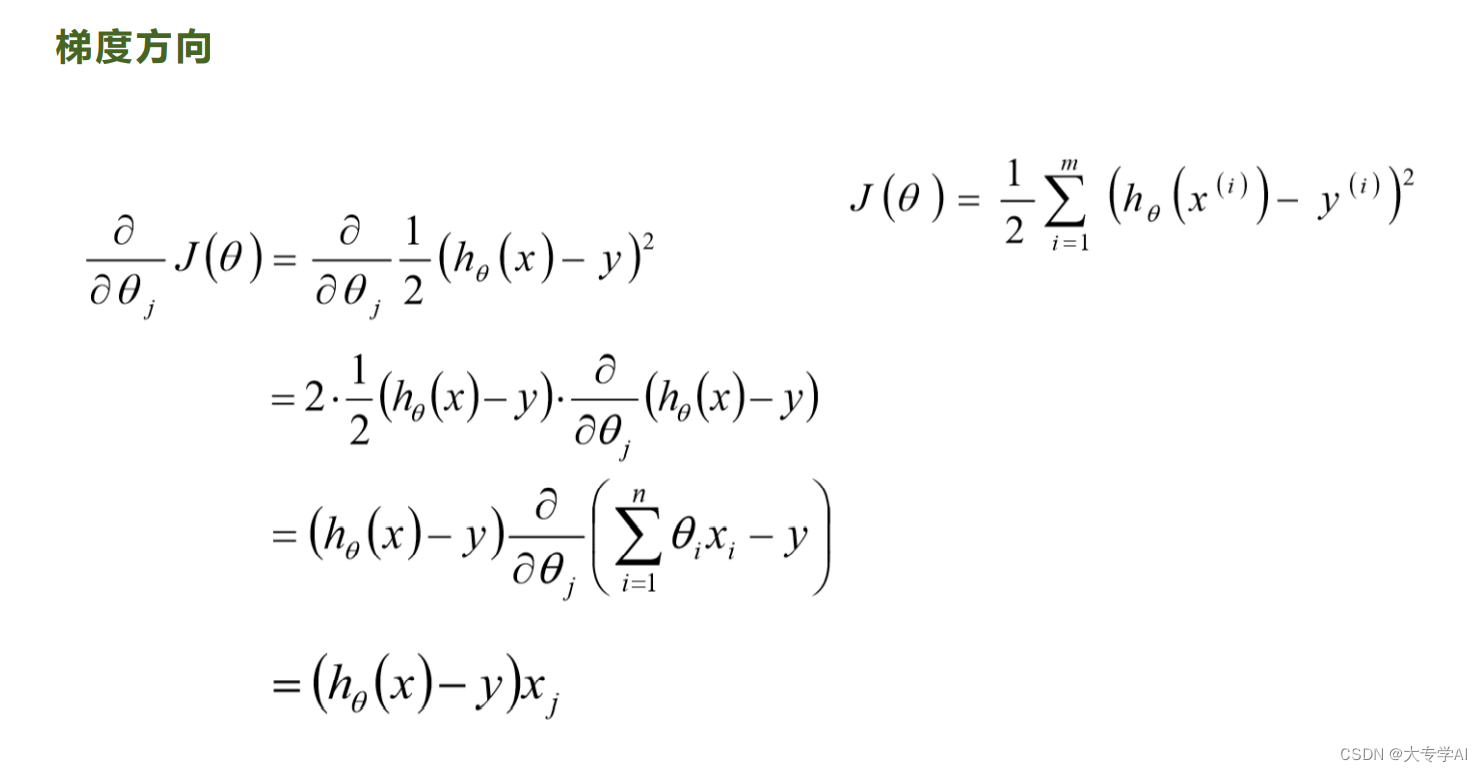
在这里插入图片描述

4.4 批量梯度下降法(BGD)

使用全部数据做梯度下降法

  1. 优点: 迭代次数最少
  2. 缺点: 训练速度慢(一次使用了全部的数据)

4.5 随机梯度下降法

  1. 优点:
  • 在学习中加入了噪声，提高了泛化误差
  • 通过自己设置batch_size 决定使用多少数据去训练，加快了每一轮的迭代速度
  1. 缺点:
  • 不收敛，容易在最小值附近波动
  • 不能再一个样本中使用向量化学习，学习过程变得很慢
  • 某一个batch的样本不能够代表全部数据
  • 由于随机性的存在可能导致最终结果比BGD差
  • 优先选择SGD

4.6 小批量梯度下降法

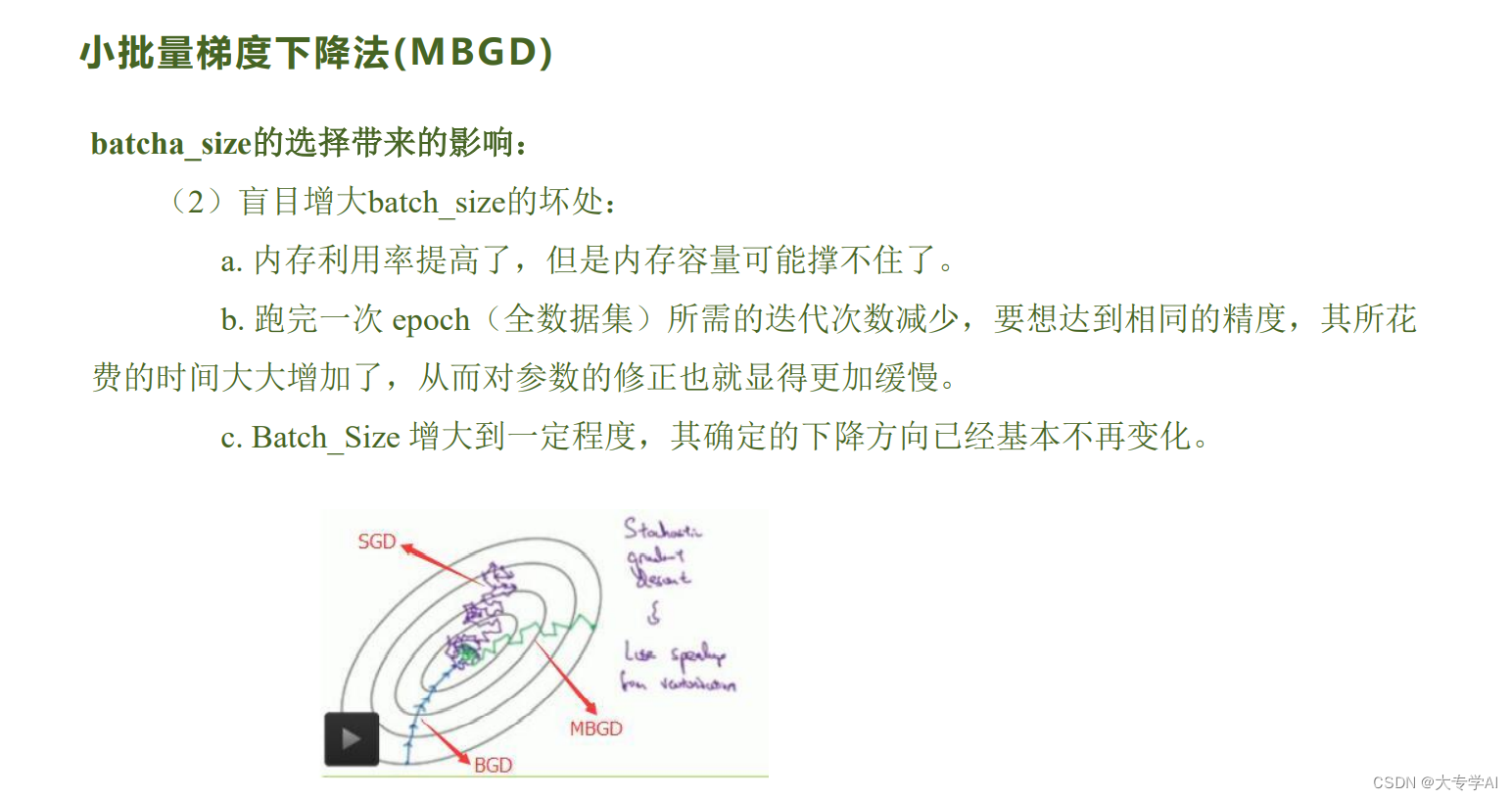
在这里插入图片描述

4.7 局部损失函数

在这里插入图片描述
当某点离要预测的点越远，其权重越小，否则越大
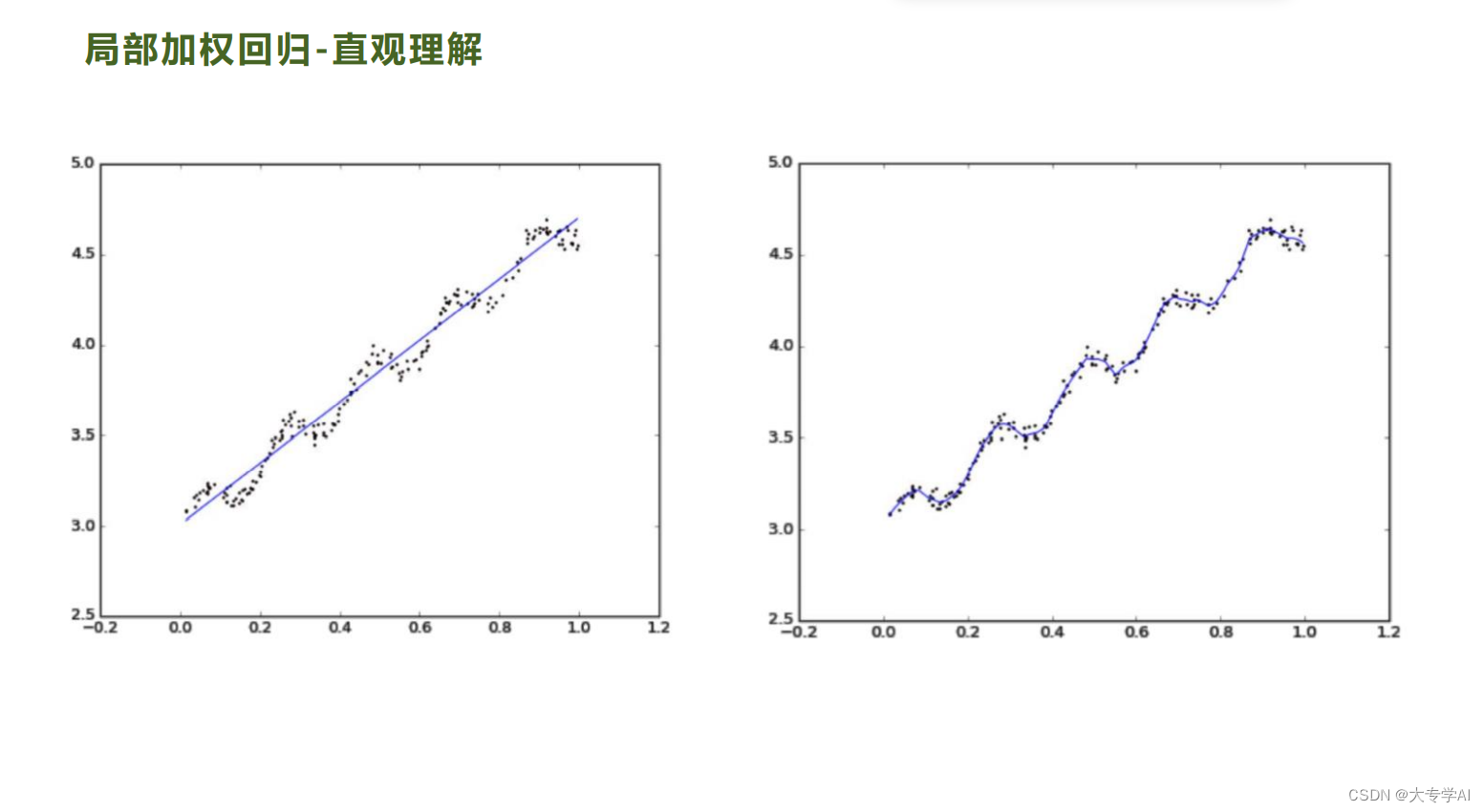
在这里插入图片描述

5. 手撕梯度下降

5.1 代码总体思路

在这里插入图片描述

5.2 需要的超参数

class LR:
    def __init__(self,data=None,learning_rate=0.01,iter_max=200,batch_size=10):
        # 初始化模型超参数
        # learning_rate=0.001,学习率一般在0.001-0.1
        # iter_max=30,设置最大迭代次数 控制模型训练停止条件
        # batch_size=1   控制梯度下降法(随机梯度下降法，批量梯度下降法小批量梯度下降法)
        self.data = data
        self.learning_rate = learning_rate
        self.iter_max = iter_max
        self.batch_size = batch_size

5.3数据预处理

在这里插入图片描述

    def data_prosses(self):
        # 数据预处理
        # 扩充常数项维度
        data = np.array(self.data)
        # 数据标准化
        # 计算均值和标准差
        mean = np.mean(data[:,:-1],axis=0)
        std = np.std(data[:,:-1],axis=0)
        data[:,:-1] = (data[:,:-1]-mean)/std
        
        one = np.ones((data.shape[0],1))
        self.data = np.hstack((one,data))
        # 训练总样本数
        self.m = self.data.shape[0]
        # 特征数 包含偏置项
        self.n = self.data.shape[1]-1

5.4 定义损失函数

    def loss(self,y_predict,y_true):
        # 定义损失函数  回归模型  使用平方损失函数
        return np.sum((y_predict-y_true)**2)

5.5 定义梯度计算公式

是计算每一个batch的平均，我们的theta是一维度的

    def cal_grad(self,y_predict,y_true,train_data):
        # 计算梯度
        self.grad = np.zeros((self.n,1))
        for i in range(self.n):
            self.grad[i,0] = np.mean((y_predict-y_true)*train_data[:,i:i+1])
        return self.grad

5.4 训练模型思路

在这里插入图片描述

    def model(self,train_data):
        # 定义算法模型
        y  = np.dot(train_data,self.theta)
        return y
    
    def tarin(self):
        # 模型训练
        n = 0   # 记录参数更新次数
        all_loss = [] # 记录每一次更新后的损失值 
        # 1、数据预处理
        self.data_prosses()
        # 2、初始化模型参数theta
        self.theta = np.random.rand(self.n,1)
        # 3、前向传播 不断训练模型
        b_n = self.m//self.batch_size   # //向下取整
        while True:
            # 每训练完一轮数据 打乱数据
            np.random.shuffle(self.data)
            for i in range(b_n):
                train_data = self.data[i*self.batch_size:(i+1)*self.batch_size]
                # 调用算法模型得到预测结果
                predict_y = self.model(train_data[:,:-1])
                # 计算损失 调用损失函数
                loss = self.loss(predict_y,train_data[:,-1:])   # train_data[:,-1:]样本真实值
                all_loss.append(loss)
                # 计算梯度  
                self.cal_grad(predict_y,train_data[:,-1:],train_data)
                # 更新参数theta的值
                self.theta = self.theta - self.learning_rate*self.grad
                n += 1 
                print(f'迭代次数:{n}\t当前误差值:{loss}\t模型参数:{self.theta}')
            # 控制模型训练停止条件
            if self.iter_max<n:
                break
        self.draw(all_loss)
        # 保存模型参数
        with open('model_lr.pt','wb') as f:
            pickle.dump(self.theta,f)

5.5 画损失函数图

    @staticmethod
    def draw(all_loss):
        plt.plot(all_loss)
        plt.show()

5.6 实验总结以及易错点

在这里插入图片描述

5.7 完整版手撕线性回归代码

#coding=utf-8
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import pickle

# 设置随机种子  保证每次初始化化值相同
np.random.seed(4)

class LR:
    def __init__(self,data=None,learning_rate=0.01,iter_max=200,batch_size=10):
        # 初始化模型超参数
        # learning_rate=0.001,学习率一般在0.001-0.1
        # iter_max=30,设置最大迭代次数 控制模型训练停止条件
        # batch_size=1   控制梯度下降法(随机梯度下降法，批量梯度下降法小批量梯度下降法)
        self.data = data
        self.learning_rate = learning_rate
        self.iter_max = iter_max
        self.batch_size = batch_size
    
    def data_prosses(self):
        # 数据预处理
        # 扩充常数项维度
        data = np.array(self.data)
        # 数据标准化
        # 计算均值和标准差
        mean = np.mean(data[:,:-1],axis=0)
        std = np.std(data[:,:-1],axis=0)
        data[:,:-1] = (data[:,:-1]-mean)/std
        
        one = np.ones((data.shape[0],1))
        self.data = np.hstack((one,data))
        # 训练总样本数
        self.m = self.data.shape[0]
        # 特征数 包含偏置项
        self.n = self.data.shape[1]-1  
    
    def model(self,train_data):
        # 定义算法模型
        y  = np.dot(train_data,self.theta)
        return y
    
    def tarin(self):
        # 模型训练
        n = 0   # 记录参数更新次数
        all_loss = [] # 记录每一次更新后的损失值 
        # 1、数据预处理
        self.data_prosses()
        # 2、初始化模型参数theta
        self.theta = np.random.rand(self.n,1)
        # 3、前向传播 不断训练模型
        b_n = self.m//self.batch_size   # //向下取整
        while True:
            # 每训练完一轮数据 打乱数据
            np.random.shuffle(self.data)
            for i in range(b_n):
                train_data = self.data[i*self.batch_size:(i+1)*self.batch_size]
                # 调用算法模型得到预测结果
                predict_y = self.model(train_data[:,:-1])
                # 计算损失 调用损失函数
                loss = self.loss(predict_y,train_data[:,-1:])   # train_data[:,-1:]样本真实值
                all_loss.append(loss)
                # 计算梯度  
                self.cal_grad(predict_y,train_data[:,-1:],train_data)
                # 更新参数theta的值
                self.theta = self.theta - self.learning_rate*self.grad
                n += 1 
                print(f'迭代次数:{n}\t当前误差值:{loss}\t模型参数:{self.theta}')
            # 控制模型训练停止条件
            if self.iter_max<n:
                break
        self.draw(all_loss)
        # 保存模型参数
        with open('model_lr.pt','wb') as f:
            pickle.dump(self.theta,f)
    
    def loss(self,y_predict,y_true):
        # 定义损失函数  回归模型  使用平方损失函数
        return np.sum((y_predict-y_true)**2)
        
    def cal_grad(self,y_predict,y_true,train_data):
        # 计算梯度
        self.grad = np.zeros((self.n,1))
        for i in range(self.n):
            self.grad[i,0] = np.mean((y_predict-y_true)*train_data[:,i:i+1])
        return self.grad
            
    @staticmethod
    def draw(all_loss):
        plt.plot(all_loss)
        plt.show()
        

if __name__ == "__main__":
    # 读取训练数据
    data = pd.read_excel(r'lr.xlsx')
    lr = LR(data)
    lr.tarin()

6. 线性回归的优化1：对数据进行归一化

主要优势: 增加迭代速度

6.1 数据归一化的必要性

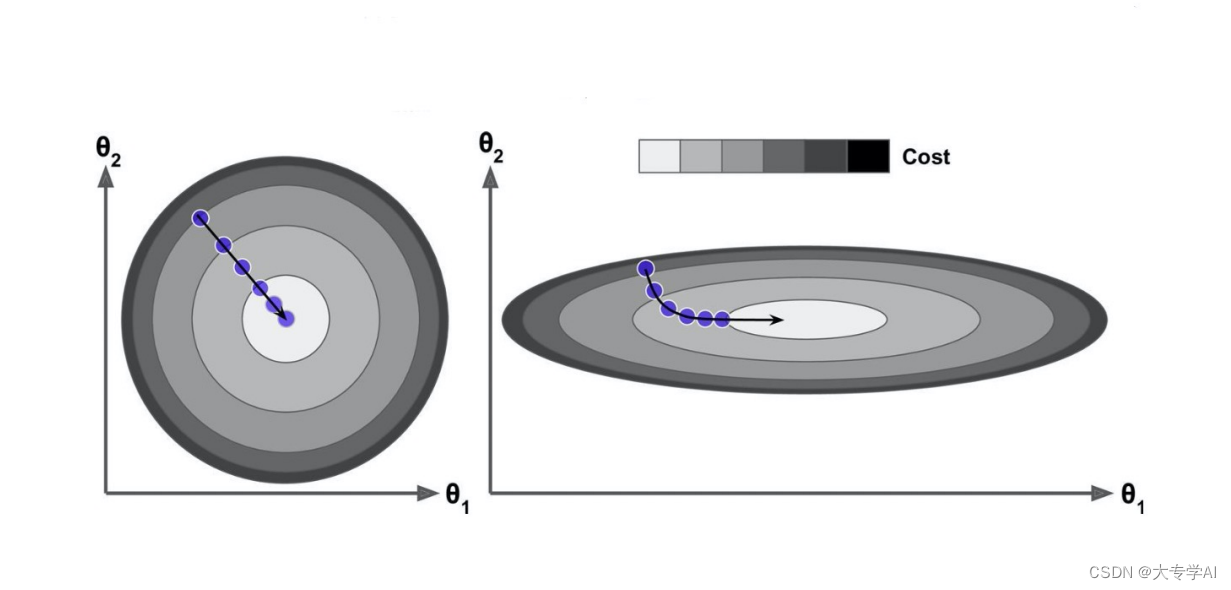
在这里插入图片描述

6.2 归一化后的速度明显增加

在这里插入图片描述

6.3 最大最小归一化

  1. 公式：
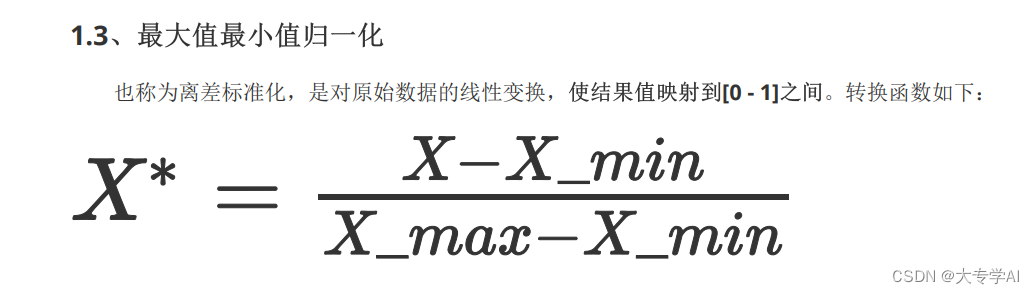
    在这里插入图片描述
  2. 代码展示
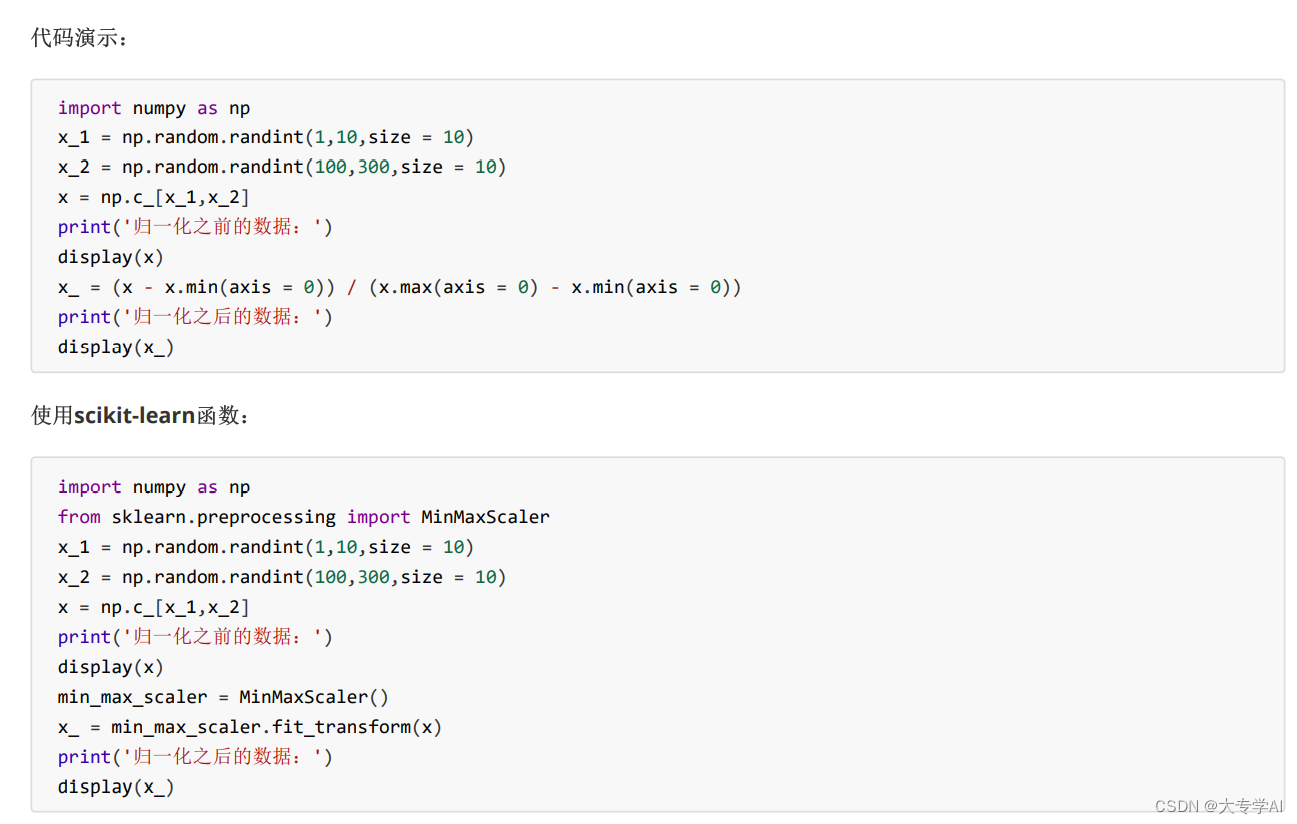
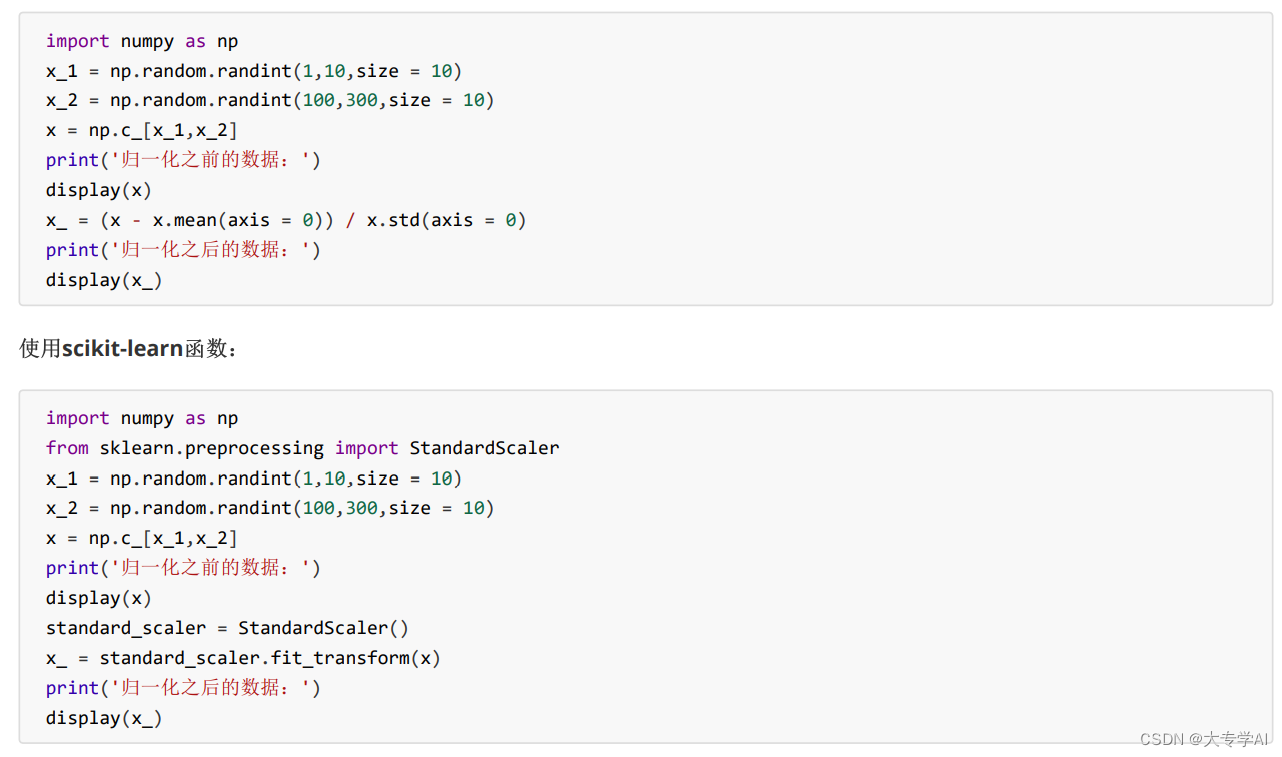
    在这里插入图片描述

6.4 Z_Score归一化

  1. 公式:
    在这里插入图片描述
  2. 代码展示：
    在这里插入图片描述

7. 线性回归优化2: 添加正则项

针对过拟合

7.1 正则项次

  1. 由于有些权重很大有些权重很小(权重的不均衡)导致了过拟合，模型越复杂，正则化项就越大
    在这里插入图片描述

7.2 L2(Ridge岭回归) 和 L1 正则（Lasso）

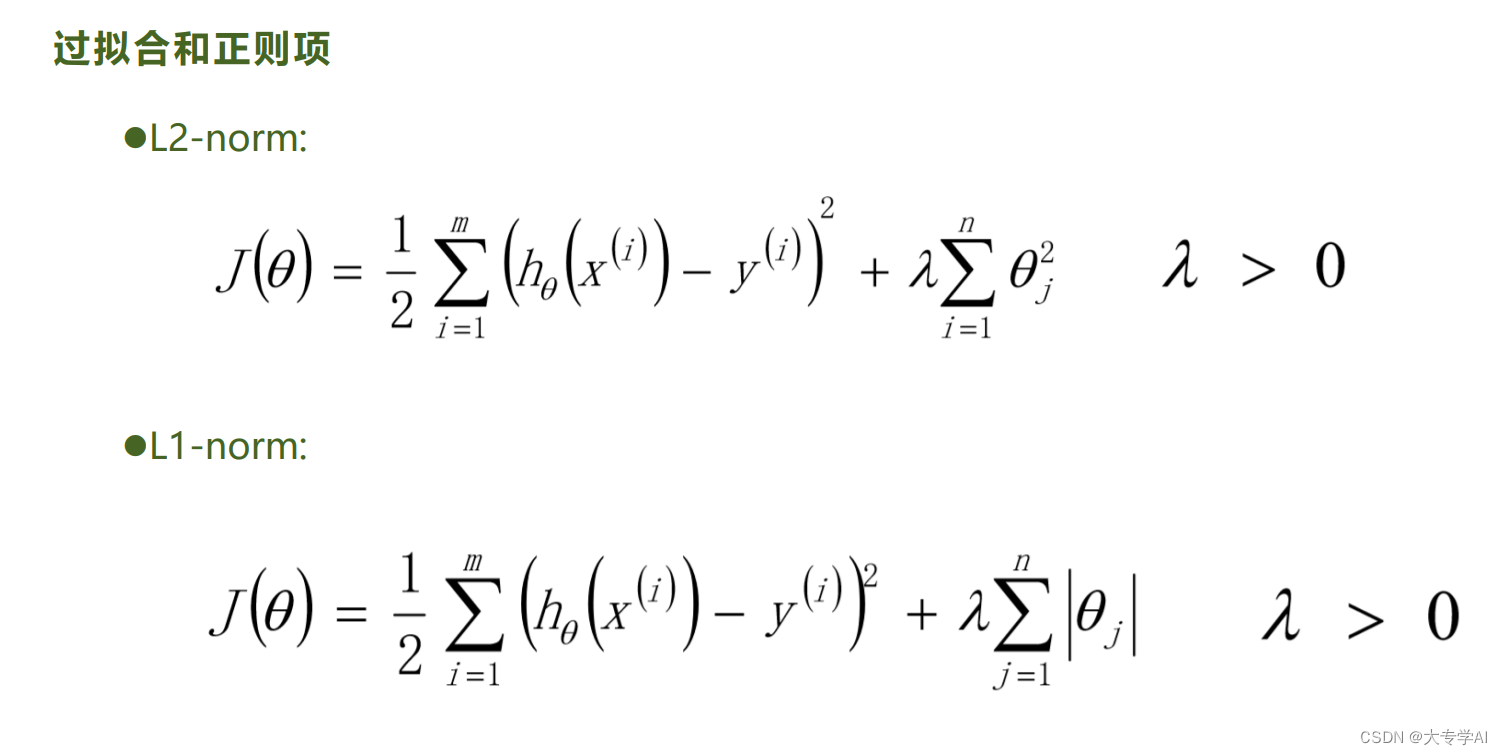
在这里插入图片描述

7.3 L1对比L2

在这里插入图片描述

7.3 Elasitic Net

L1 + L2

8. 线性回归优化3: 多项式回归

8.1 做多项式拓展的原因： 解决欠拟合

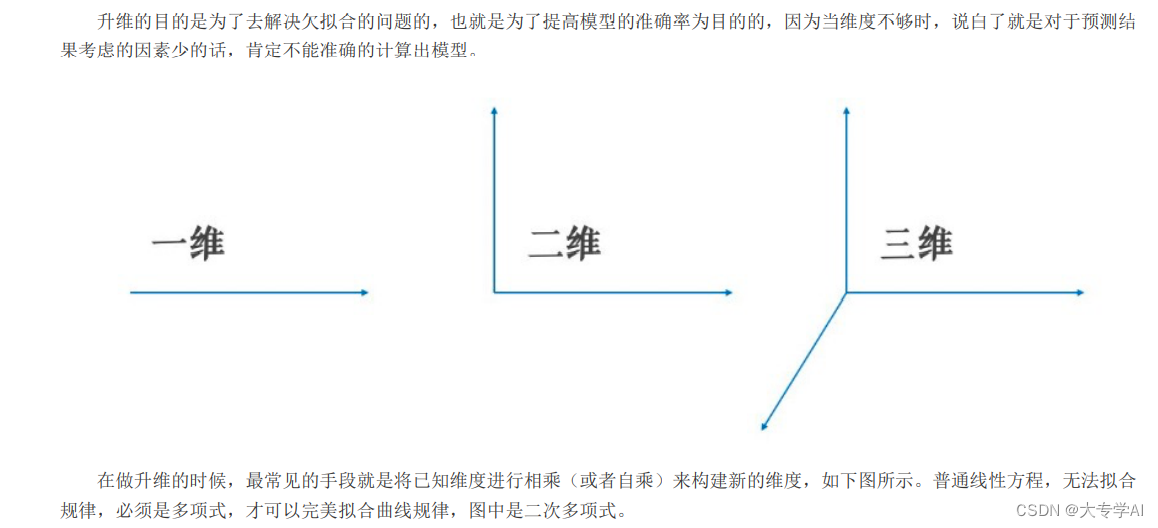
在这里插入图片描述

8.2 并不是阶数越高越好

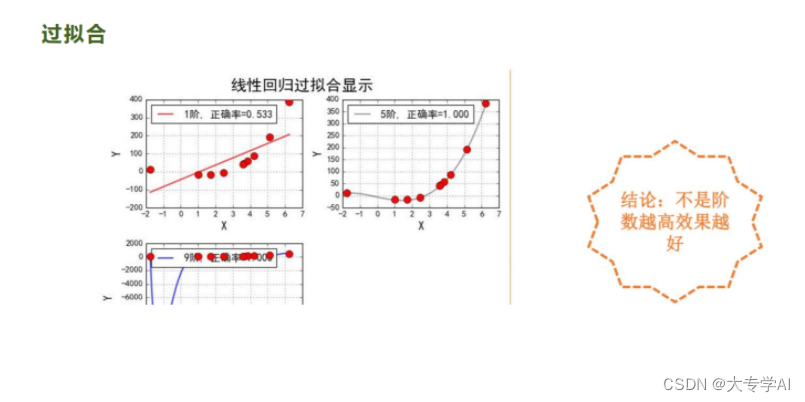
在这里插入图片描述

8.3 简单案例展示

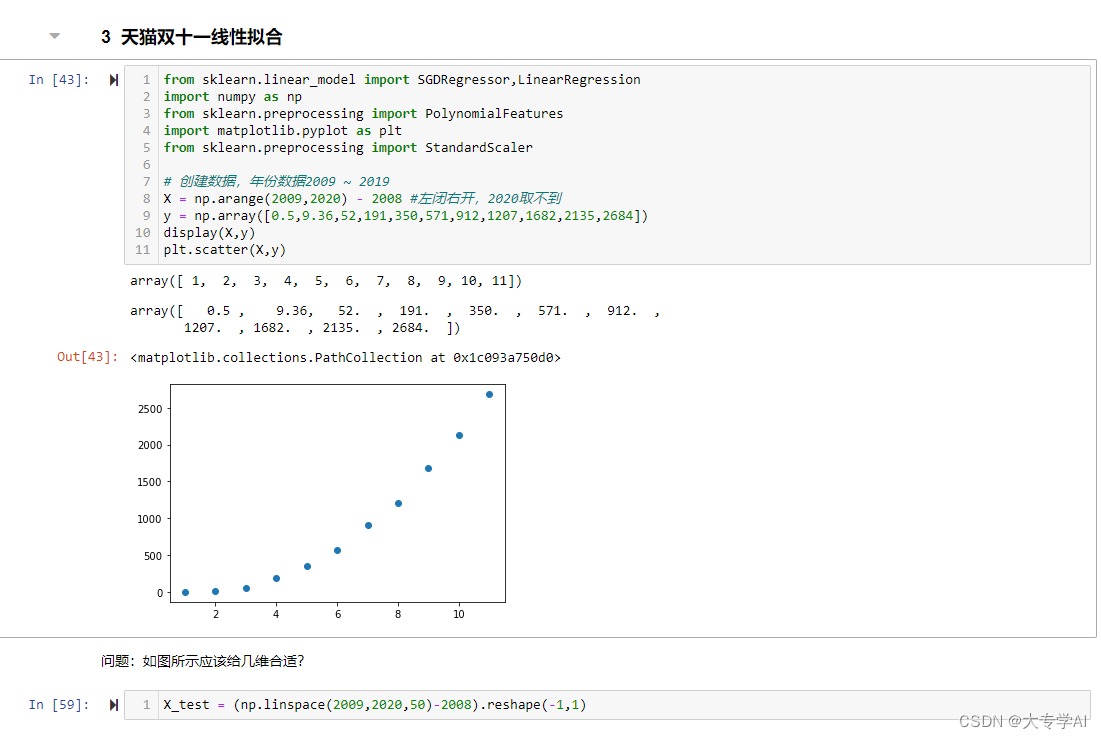
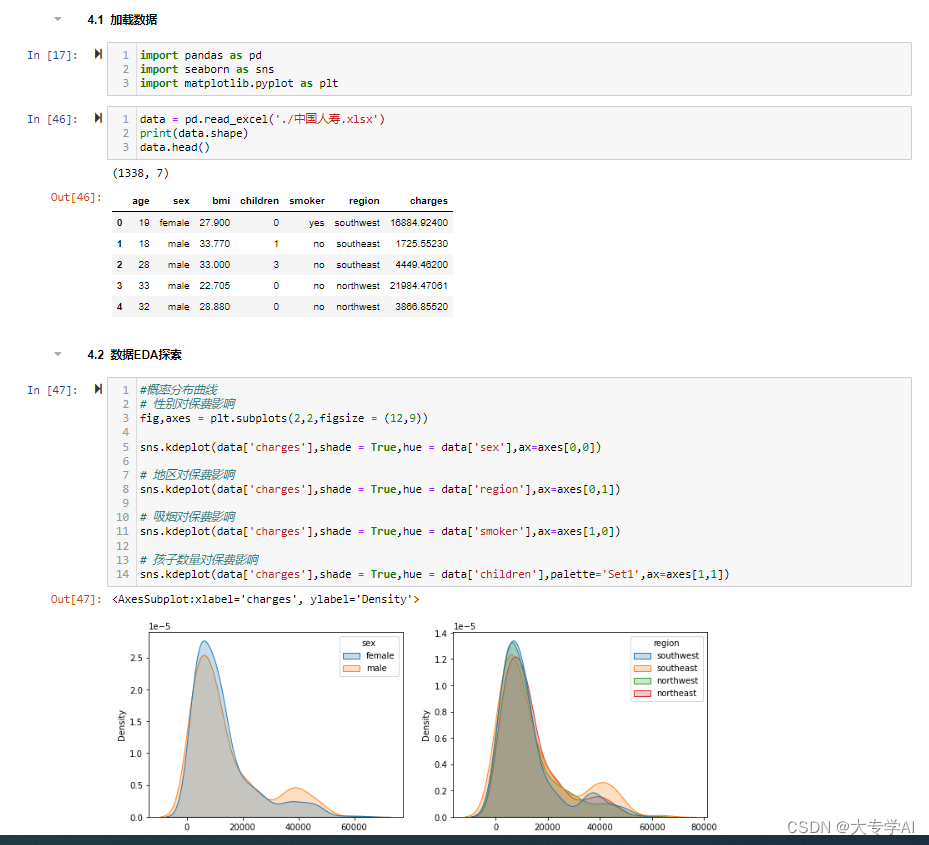
在这里插入图片描述
在这里插入图片描述

9. 通过一个比赛来练习学习的东西(天池大赛蒸汽预测的回归任务)

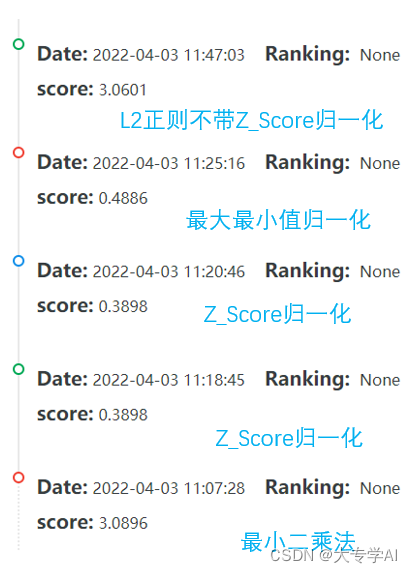
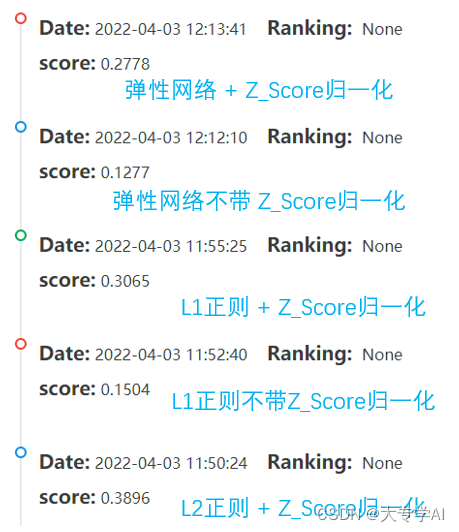
  1. 代码弄丢了，懒得写了，看看结果就好，反正代码很好写的
  2. 最终的最好的结果是弹性网络不带正则化的
    在这里插入图片描述
    在这里插入图片描述
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值