1.CART算法与决策树算法
决策树算法的基础算法有ID3算法、C4.5算法、CART算法三种。其中前两种均是由罗斯昆(J Ross Quinlan)提出。CART算法由Breiman等人在 1984 年提出的一种二叉树模型。与前两种算法不同的是,CART算法仅是二叉树模型,不过在具体的实现过程中,可以通过多层二叉树实现多叉树。此外,前两种算法仅支持分类树,不支持回归树;而CART算法不仅支持分类树,也支持回归树。
三种决策树算法在有监督机器学习模型中有着重要的地位,是诸多模型的基础算法。其中,CART算法因其自身的特点和优势,有着更广泛的应用。
2.CART算法的核心原理
本文介绍CART算法中的分类树。
CART分类树采用基尼指数(基尼不纯度、基尼系数)作为分裂的依据。这与ID3算法、C4.5算法有着较大不同。信息熵的计算需要用到对数运算,而基尼指数的计算仅需要四则运算,计算效率相对较高。
以下讲解一下基尼指数。
2.1 基尼指数的定义
分类的目的是尽可能找到一个“准确率”比较高的分类,基尼指数可以用于衡量分类的”准确率”。
假设随机事件共有K个类别,每个类别发生的概率为,则其基尼不纯度为:
从上述定义可以看出,当越大时,基尼指数越低,分类越“准确”。
对于二分类事件来说,=2。
2.2 基尼指数的计算
数据集D,特征A在其属性上将其划分为两部分,则集合D在特征A条件下的基尼指数为:
其中表示各样本集中样本的数量。
3.CART算法过程
3.1 输入与输出
输入:训练数据集,特征集
,分裂停止条件:样本数量或基尼指数小于指定的分裂阈值,不妨将值记为
。其中训练数据集
中包括分类值(可以类似理解为目标值、被解释变量等)。
输出:决策树
3.2 算法过程
3.2.1 节点预判断
1)若该节点的数据集中所有实例都属于同一类
, 则以
作为此节点的分类,此节点分裂结束;
2)若该节点的数据集中所有实例无任何特征,以
中实例类别数量最多的
作为此节点的实例分类,此节点分裂结束。
否则进入下一步。
3.2.2 选择分裂特征
在该分裂的样本集下,计算每一个特征在其所有属性的基尼指数。由于CART分类算法是二分类,若该特征有多于2个属性,需要将其属性组合成两个类别(根据
的判断将其分为两个类别),再分别计算所有可能组合的基尼指数。
Tips:若该特征有J个属性,所有组合其实是将其分为两组的所有划分。若有2个属性,仅有1个划分;若有3个属性,则有3个划分;若有4个属性,则有7个划分;若有5个属性,则有15个划分。
以基尼指数最小的特征为该节点的分裂特征,进入下一步。若有两个以上相同的基尼指数,可随机选择其一个作为分裂节点。需要注意的是,不同的分裂选择,生成树的形状会不一样,甚至有很大的差异。
若所有特征的基尼指数<,则该节点分裂停止。
3.2.3 节点分类
按该特征的属性按上述分裂产生子节点,各子节点中以实例类别数量最多的作为各子节点的类别。
3.2.4 继续分裂
对上一步产生的各子节点,返回第1步循环(递归调用)。直至所有节点分裂结束。
Tips:与ID3算法、C4.5算法不同的是,CART算法在分裂中同一特征可以被多次使用。比如,在上一层分裂中已使用过的特征,可以在下一层分裂中继续使用。不过,上层分裂中已使用的属性组合不会在其下层分裂中使用。
4.CART算法演示
本部分算法演示选择与ID3算法原理详解_blinkyou001的博客-优快云博客文中相同的例子进行演示。不过,为了简化过程,此处演示减少一个特征,只保留前4个特征。
以客户的申请信息来判断是否给予贷款。涉及的特征有年龄、性别、收入、房产、审批结果,前4个特征分别记为。以此数据集为样本,记为
。
4.1 数据集
| 序号 | 年龄 | 性别 | 收入 | 房产 | 审批结果 |
| 1 | 青年 | 男 | 高 | 有 | 通过 |
| 2 | 青年 | 男 | 中 | 无 | 通过 |
| 3 | 青年 | 男 | 低 | 无 | 拒绝 |
| 4 | 青年 | 女 | 中 | 有 | 通过 |
| 5 | 青年 | 女 | 低 | 无 | 通过 |
| 6 | 中年 | 男 | 高 | 有 | 拒绝 |
| 7 | 中年 | 男 | 中 | 无 | 拒绝 |
| 8 | 中年 | 女 | 高 | 有 | 通过 |
| 9 | 中年 | 女 | 中 | 有 | 通过 |
| 10 | 中年 | 女 | 低 | 无 | 拒绝 |
| 11 | 老年 | 男 | 高 | 有 | 通过 |
| 12 | 老年 | 男 | 低 | 有 | 通过 |
| 13 | 老年 | 男 | 低 | 无 | 拒绝 |
| 14 | 老年 | 女 | 中 | 无 | 通过 |
| 15 | 老年 | 女 | 高 | 有 | 拒绝 |
4.2 算法步骤
4.2.1 第一层分裂
样本数据的分类,即“审批结果”有两个类别:通过、拒绝,并非同一类,需要分裂。
计算每一个特征的基尼指数。
1)年龄的基尼指数
年龄有三个属性:青年、中年、老年,共有3种组合,分别计算其基尼指数。
a. 青年、中年老年
青年的基尼指数
中年老年的基尼指数
第1个特征第1种属性组合的基尼指数:
=0.44
b.中年、青年老年
中年的基尼指数
中年老年的基尼指数
第1个特征第2种属性组合的基尼指数:
c.老年、青年中年
老年的基尼指数
中年老年的基尼指数
第1个特征第3种属性组合的基尼指数:
2)性别的基尼指数
a.男
b.女
第2个特征的基尼指数:
3)收入的基尼指数
收入有三个属性:高、中、低,共有3种组合,分别计算其基尼指数。
a.高、中低
高的基尼指数
中低的基尼指数
第3个特征第1种组合的基尼指数:
b.中、高低
中的基尼指数
高低的基尼指数
第3个特征第2种组合的基尼指数:
c.低、高中
低的基尼指数
高中低的基尼指数
第3个特征第3种组合的基尼指数:
4)房产的基尼指数
收入有两个属性:有、无,分别计算其基尼指数。
a.有
b.无
第4个特征的基尼指数:
上述4个特征的基尼指数如下表:
| 序号 | 特征 | 基尼指数 |
| 1 | 年龄 | 0.44,0.44,0.48 |
| 2 | 性别 | 0.4571 |
| 3 | 收入 | 0.48,0.44,0.44 |
| 4 | 房产 | 0.4286 |
上述所有特征的基尼指数中,第4个特征“房产”的基尼指数最小,以该特征作为分裂特征。特征选择完成。
该分裂节点的分类。“有”属性中,类别最多的为的为“通过”,该属性归类为“通过”;“无”属性中,类别最多的为的为“拒绝”,该属性归类为“拒绝”
4.2.2 进一步分裂
分别对房产特征的两个属性作为预判断,再决定是否继续分裂。该特征两个属性均有不同类别,需要继续分裂。(若基尼指数小于指定,本节点分裂可停止)
1)房产:有
| 序号 | 年龄 | 性别 | 收入 | 审批结果 |
| 1 | 青年 | 男 | 高 | 通过 |
| 4 | 青年 | 女 | 中 | 通过 |
| 6 | 中年 | 男 | 高 | 拒绝 |
| 8 | 中年 | 女 | 高 | 通过 |
| 9 | 中年 | 女 | 中 | 通过 |
| 11 | 老年 | 男 | 高 | 通过 |
| 12 | 老年 | 男 | 低 | 通过 |
| 15 | 老年 | 女 | 高 | 拒绝 |
分别计算各特征的最小基尼指数,如下:
| 特征 | Gini | |
| 0 | 年龄 | 0.333333 |
| 1 | 性别 | 0.375 |
| 2 | 收入 | 0.3 |
上述所有特征的基尼指数中,第3个特征“收入”的基尼指数最小,以该特征为分裂特征。特征选择完成。
该分裂节点的分类。收入有3个组合,其中“高、中低”组合的基尼指数最小为0.3,以此进一步分裂。“高”属性中,类别最多的为的为“通过”,该属性归类为“通过”;“中低”属性中,类别最多的为的为“通过”,该属性归类为“通过”。
1.1)收入:高
| 序号 | 年龄 | 性别 | 收入 | 审批结果 |
| 1 | 青年 | 男 | 高 | 通过 |
| 6 | 中年 | 男 | 高 | 拒绝 |
| 8 | 中年 | 女 | 高 | 通过 |
| 11 | 老年 | 男 | 高 | 通过 |
| 15 | 老年 | 女 | 高 | 拒绝 |
分别计算各特征的最小基尼指数,如下:
| 特征 | Gini | |
| 0 | 年龄 | 0.4 |
| 1 | 性别 | 0.466667 |
上述所有特征的基尼指数中,第1个特征“年龄”的基尼指数最小,以该特征为分裂特征。特征选择完成。
该分裂节点的分类。年龄有3个组合,其中“青年、老年中年”组合的基尼指数最小为0.4,以此进一步分裂。“青年”属性中,唯一的类别为“通过”,该属性归类为“通过”;“老年中年”属性中,类别“通过”与“拒绝”一样多,可随机选择一个,不妨将属性归类为“通过”。
1.1.1)年龄:青年
青年属性中,仅有一个类别“通过”。分裂结束。
1.1.2)年龄:中年老年
| 序号 | 年龄 | 性别 | 收入 | 审批结果 |
| 6 | 中年 | 男 | 高 | 拒绝 |
| 8 | 中年 | 女 | 高 | 通过 |
| 11 | 老年 | 男 | 高 | 通过 |
| 15 | 老年 | 女 | 高 | 拒绝 |
分别计算各特征的最小基尼指数(此时收入仅有一个属性,无需分裂),如下:
| 特征 | Gini | |
| 0 | 年龄 | 0.5 |
| 1 | 性别 | 0.5 |
两年特征的基尼指数相同,随机选择“年龄”作为分裂特征。
该分裂节点的分类。此时,“年龄”属性仅剩中年、老年一种组合,以此进一步分裂。“中年”属性中,审批结果的类别相同,不妨选择该属性归类为“通过”;“老年”属性中,审批结果的类别相同,不妨选择该属性归类为“拒绝”。
1.1.2.1)年龄:中年
| 序号 | 年龄 | 性别 | 审批结果 |
| 6 | 中年 | 男 | 拒绝 |
| 8 | 中年 | 女 | 通过 |
剩余的特征“性别”的两个属性分别只有一个分类。分裂结束。
1.1.2.2)年龄:老年
| 序号 | 年龄 | 性别 | 审批结果 |
| 11 | 老年 | 男 | 通过 |
| 15 | 老年 | 女 | 拒绝 |
剩余的特征“性别”的两个属性分别只有一个分类。分裂结束。
1.2)收入:中低
| 序号 | 年龄 | 性别 | 收入 | 审批结果 |
| 4 | 青年 | 女 | 中 | 通过 |
| 9 | 中年 | 女 | 中 | 通过 |
| 12 | 老年 | 男 | 低 | 通过 |
该特征下样本分类相同,分裂结束。
所有类别均为“通过”。
2)房产:无
| 年龄 | 性别 | 收入 | 审批结果 | |
| 1 | 青年 | 男 | 中 | 通过 |
| 2 | 青年 | 男 | 低 | 拒绝 |
| 4 | 青年 | 女 | 低 | 通过 |
| 6 | 中年 | 男 | 中 | 拒绝 |
| 9 | 中年 | 女 | 低 | 拒绝 |
| 12 | 老年 | 男 | 低 | 拒绝 |
| 13 | 老年 | 女 | 中 | 通过 |
分别计算各特征的最小基尼指数,如下:
| 特征 | Gini | |
| 0 | 年龄 | 0.342857 |
| 1 | 性别 | 0.404762 |
| 2 | 收入 | 0.404762 |
上述所有特征的基尼指数中,第1个特征“年龄”的基尼指数最小,以该特征为分裂特征。特征选择完成。
该分裂节点的分类。年龄有3个组合,其中“中年、老年青年”组合的基尼指数最小为0.342857,以此进一步分裂。“中年”属性中,唯一的类别为“拒绝”,该属性归类为“拒绝”;“老年青年”属性中,类别“通过”最多,该属性归类为“通过”。
2.1)年龄:中年
该特征下样本分类相同,分裂结束。
所有类别均为“拒绝”。
2.2)年龄:老年青年
| 年龄 | 性别 | 收入 | 审批结果 | |
| 1 | 青年 | 男 | 中 | 通过 |
| 2 | 青年 | 男 | 低 | 拒绝 |
| 4 | 青年 | 女 | 低 | 通过 |
| 12 | 老年 | 男 | 低 | 拒绝 |
| 13 | 老年 | 女 | 中 | 通过 |
分别计算各特征的最小基尼指数,如下:
| 特征 | Gini | |
| 0 | 年龄 | 0.466667 |
| 1 | 性别 | 0.266667 |
| 2 | 收入 | 0.266667 |
上述所有特征的基尼指数中,第2个特征“年龄”和第3个特征“收入”的基尼指数均最小,不妨选择性别为分裂特征。特征选择完成。
该分裂节点的分类。性别有1个组合,其基尼指数为0.266667,以此进一步分裂。“男”属性中最多的类别为“拒绝”,该属性归类为“拒绝”;“女”属性类别均“通过”,该属性归类为“通过”。
2.2.1)性别:男
| 年龄 | 收入 | 审批结果 | |
| 1 | 青年 | 中 | 通过 |
| 2 | 青年 | 低 | 拒绝 |
| 12 | 老年 | 低 | 拒绝 |
分别计算各特征的最小基尼指数,如下:
| 特征 | Gini | |
| 0 | 年龄 | 0.333333 |
| 1 | 收入 | 0 |
上述所有特征的基尼指数中,第3个特征“收入”的基尼指数均最小,为分裂特征。特征选择完成。
该分裂节点的分类。收入的两个属性,分别只有一个分类。“中”属性中的类别为“通过”,该属性归类为“通过”;“低”属性类别均“拒绝”,该属性归类为“拒绝”。分裂结束。
2.2.2)性别:女
该特征下样本分类相同,分裂结束。
所有类别均为“通过”。
至此,所有节点分裂结束,完成分裂。
4.3 分裂图示
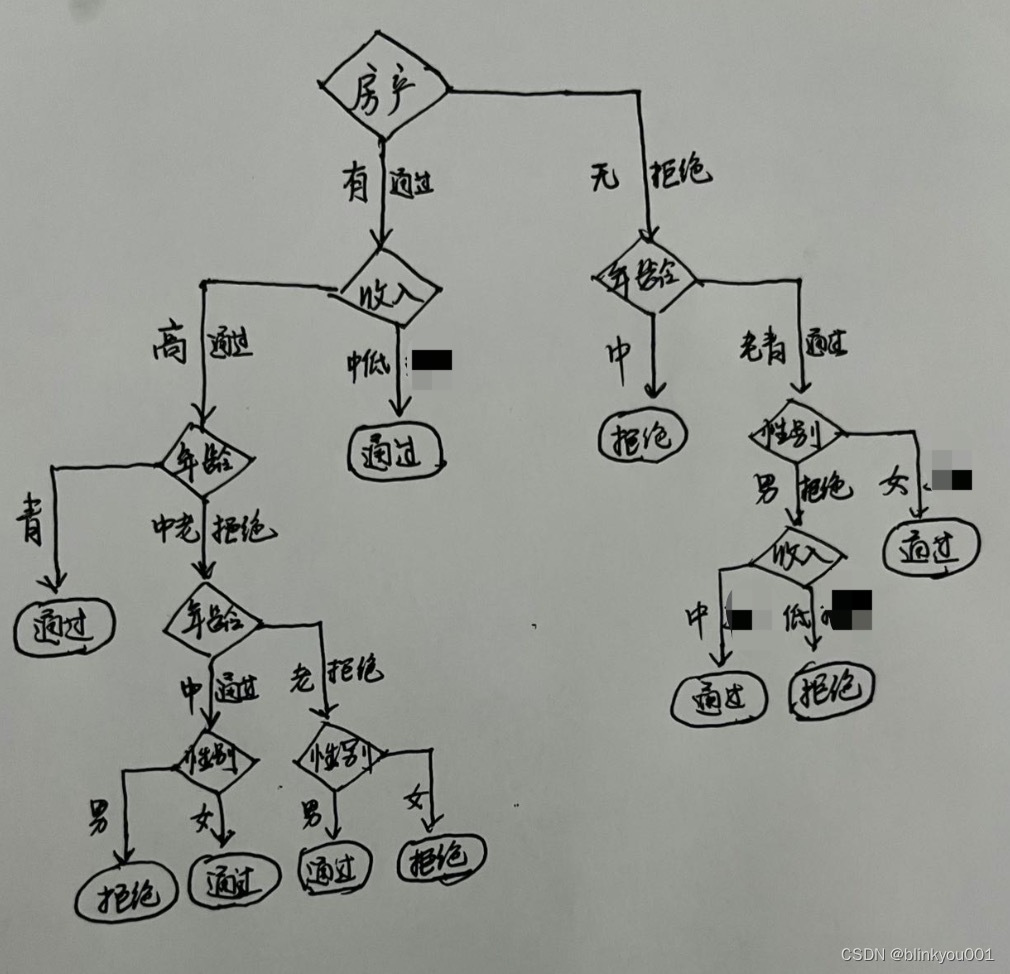
连接线的左边表示属性,右边表示分类。
5.CART分类算法总结
CART算法有着非常广泛的应用。
1)CART分类算法是二叉树。这与ID3算法、C4.5算法均不同,这两个算法均是多叉树。
2)CART分类算法中决策树分类的主要依据是基尼指数。ID3算法、C4.5算法分别是信息增益、信息增益比。
3)CART算法的基尼指数的计算使用的是四则运算,而ID3算法和C4.5算法使用了大量的对数运算,CART算法的运算效率相对较高。
4)CART算法支持剪枝,采用的是后剪枝。





















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








