栈与队列理论基础



stack和queue不是容器container而是容器适配器container adapter
不提供迭代器不能随机访问
栈的底层实现可以是vector,deque,list
注意queue和deque的差别

deque是双开口容器,类比vector,内存是连续空间的block用指针连接起来的分段内存,vector是连续内存,deque查找效率比vector高
232.用栈实现队列
思路:
用两个栈模拟一个队列
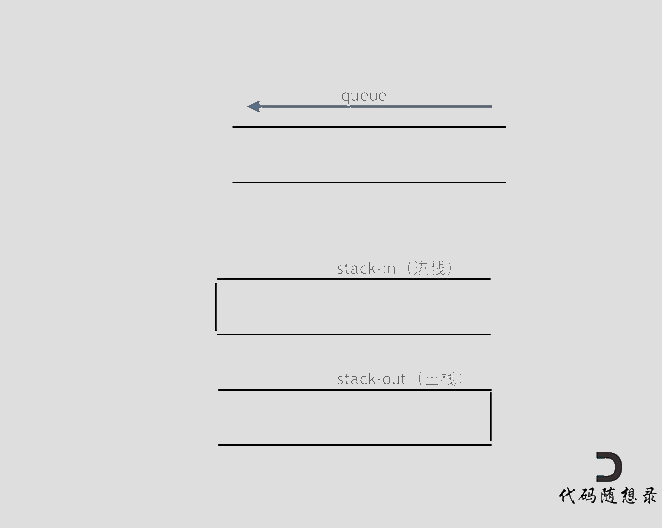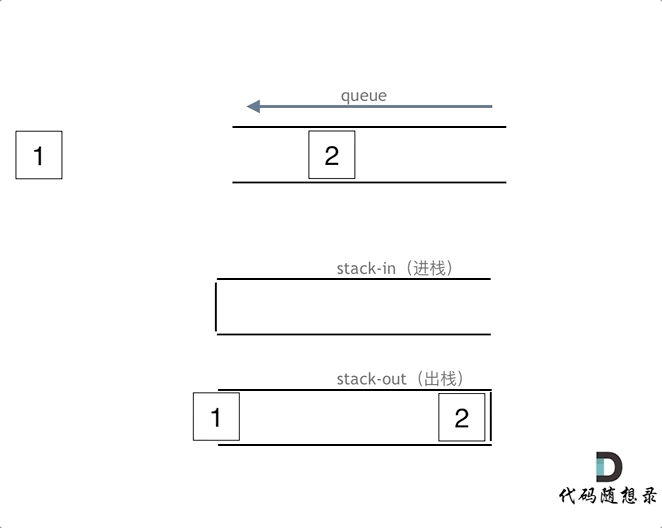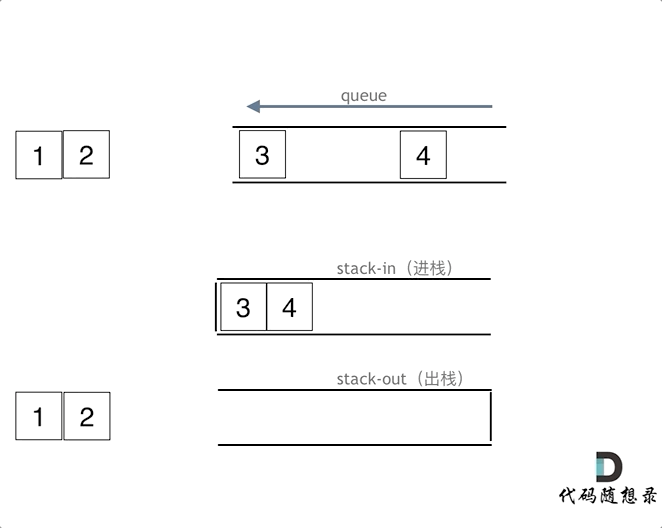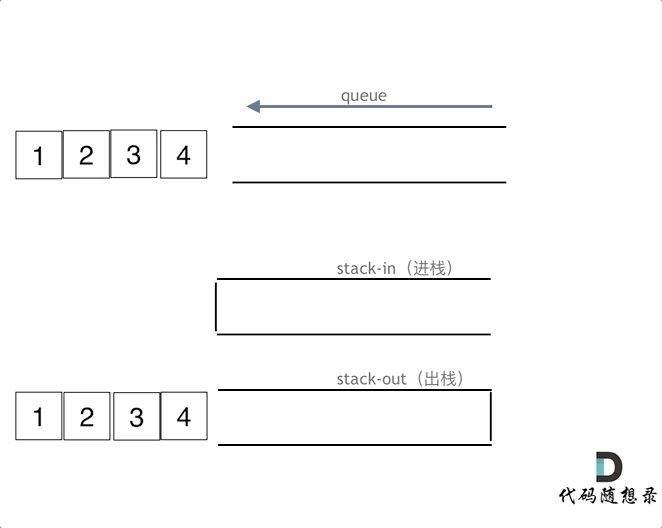
入队模拟:push到输入栈
出队模拟:输入栈pop到输出栈,输出栈再pop
空队判断:两个栈都弹空
注意pop不返回元素不能用int接受 :
int res = stack_out.pop(); ×
int res = stack_out.top(); stack_out.pop(); √
class MyQueue {
public:
// 用两个栈模拟队列
stack<int> stack_in; // 输出栈
stack<int> stack_out; // 输出栈
MyQueue() {
}
void push(int x) {
stack_in.push(x);
}
int pop() {
// 输出栈为空,把输入栈的top弹出,输出栈入栈
if(stack_out.empty())
{
int tmp = stack_in.top();
stack_in.pop();
stack_out.push(tmp);
}
// 弹出输出栈栈顶
int res = stack_out.top();
stack_out.pop();
return res;
}
int peek() {
int res = pop(); // 用pop拿到的输出栈栈顶就是队列的队头
stack_out.push(res); // 函数是查找功能,pop是弹出功能,所以这里把弹出的元素再push回去
return res;
}
bool empty() {
return stack_in.empty() && stack_out.empty();
}
};225. 用队列实现栈
思路:
用一个队列来模拟栈
一个队列在模拟栈弹出元素的时候只要将队列头部的元素(除了最后一个元素外) 重新添加到队列尾部,此时再去弹出元素就是栈的顺序了。

20. 有效的括号
思路:
只有三种出错情况:多了左括号,多了右括号,左右括号不匹配
用栈结构模拟三种情况,遇到左括号放右括号入栈,遇到右括号开始栈自顶向下判断是否匹配
class Solution {
public:
bool isValid(string s) {
if (s.size() % 2 != 0) return false; // 如果s的长度为奇数,一定不符合要求
stack<char> st;
for (int i = 0; i < s.size(); i++) {
if (s[i] == '(') st.push(')');
else if (s[i] == '{') st.push('}');
else if (s[i] == '[') st.push(']');
// 第三种情况:遍历字符串匹配的过程中,栈已经为空了,没有匹配的字符了,说明右括号没有找到对应的左括号 return false
// 第二种情况:遍历字符串匹配的过程中,发现栈里没有我们要匹配的字符。所以return false
else if (st.empty() || st.top() != s[i]) return false;
else st.pop(); // st.top() 与 s[i]相等,栈弹出元素
}
// 第一种情况:此时我们已经遍历完了字符串,但是栈不为空,说明有相应的左括号没有右括号来匹配,所以return false,否则就return true
return st.empty();
}
};1047. 删除字符串中的所有相邻重复项
class Solution {
public:
string removeDuplicates(string S) {
stack<char> st;
for (char s : S) {
if (st.empty() || s != st.top()) {
st.push(s);
} else {
st.pop(); // s 与 st.top()相等的情况
}
}
string result = "";
while (!st.empty()) { // 将栈中元素放到result字符串汇总
result += st.top();
st.pop();
}
reverse (result.begin(), result.end()); // 此时字符串需要反转一下
return result;
}
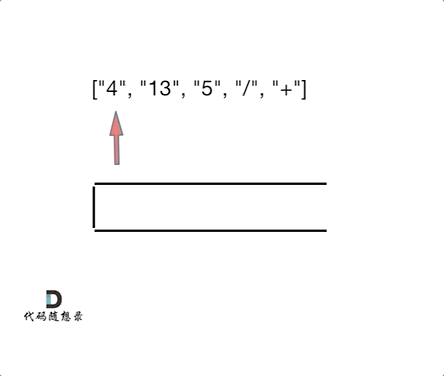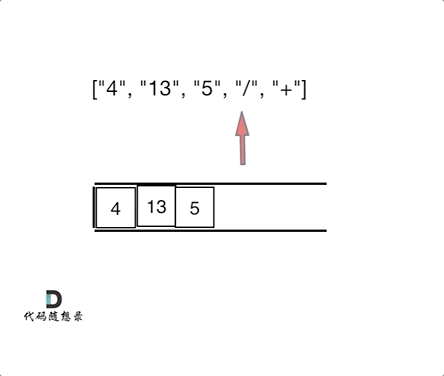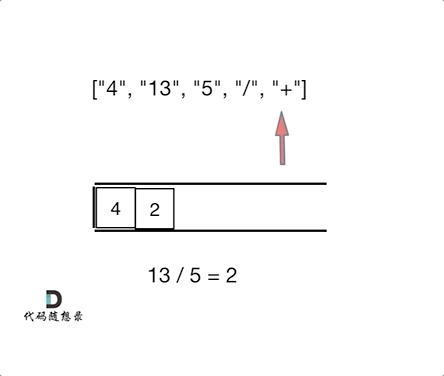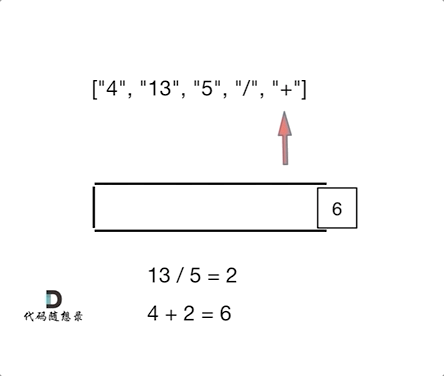
};150. 逆波兰表达式求值
思路:
逆波兰表达式是一种后需遍历,可以用栈来解决
遇到数字就入栈,遇到符号就从栈取两个数字进行操作,将结果入栈
使用std::stoi, std::stol, std::stoll, std::stoul, std::stoull等函数可将string转为int, long, long long ,unsigned long, unsigned long long
int evalRPN(vector<string>& tokens) {
stack<int> MyStack;
for(int i = 0; i < tokens.size(); ++i)
{
if(tokens[i] !="+" && tokens[i] !="-" &&
tokens[i] !="*" && tokens[i] !="/")
{
MyStack.push(stoi(tokens[i]));
continue;
}
if(MyStack.size() < 2) continue;
int num1 = MyStack.top();
MyStack.pop();
int num2 = MyStack.top();
MyStack.pop();
if(tokens[i] == "+")
{
MyStack.push(num2 + num1);
}
else if(tokens[i] == "-")
{
MyStack.push(num2 - num1);
}
else if(tokens[i] == "*")
{
MyStack.push(num2 * num1);
}
else if(tokens[i] == "/")
{
MyStack.push(num2 / num1);
}
else
{
}
}
if(!MyStack.empty())
{
return MyStack.top();
}
return -1;
}239. 滑动窗口最大值
思路1:
用multiset将窗口内的k个元素构成有序子集,每次删掉上一个元素,新加一个新元素,multiset会自动按从小到大排序
注意map和set没有pop和push,只有insert和erase。没有front和back,返回最后一个元素可以对rbeign()迭代器取值,不要用end(),end指向最后一个元素下一个空位置
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
vector<int> res;
multiset<int> MySet;
for(int i = 0; i < nums.size();++i)
{
if(i < k )
{
MySet.insert(nums[i]);
if(i == k - 1 ) res.push_back(*MySet.rbegin());
continue;
}
auto it = find(MySet.begin(), MySet.end(), nums[i - k]);
if(it != MySet.end()) MySet.erase(it);
MySet.insert(nums[i]);
res.push_back(*MySet.rbegin());
}
return res;
}可能会超时
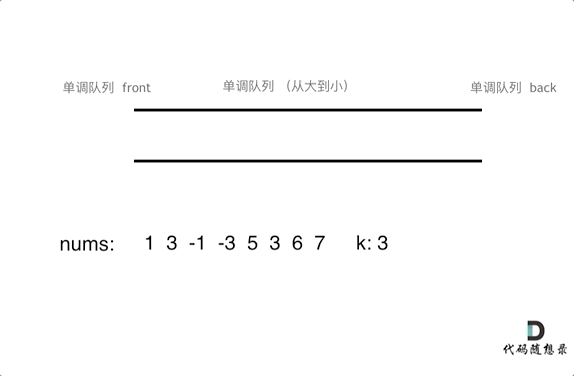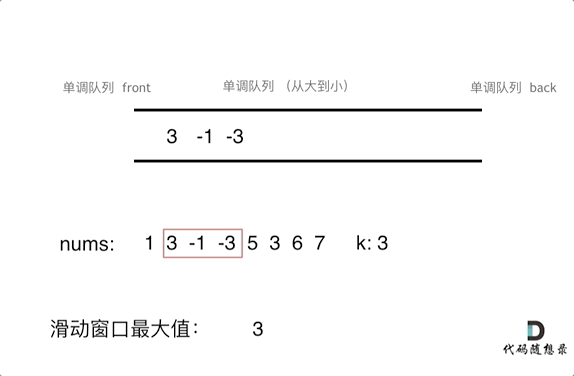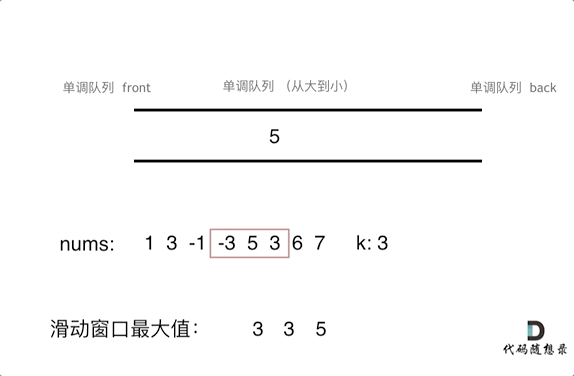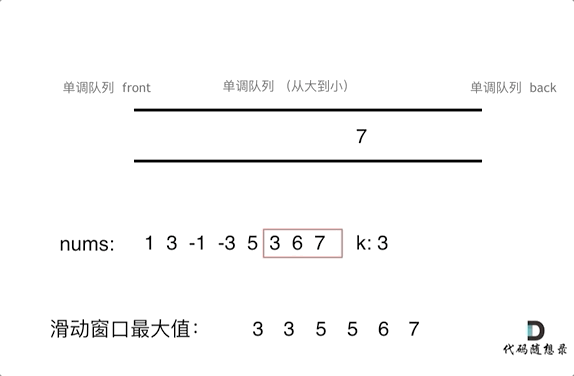
思路2:
用队列模仿k窗口的滑动,队列放入k个值,滑动窗口就是pop队头,push新值到队尾,然后求max
push新值时入队时,如果前面值比入队值小则pop,这样保证队头是max值
pop时要判断弹出的值是否是队头,是则弹出,不是说明之前入队时就被弹走了
这里用deque双头队列,而不是queue单调队列
class Solution {
private:
class MyQueue { //单调队列(从大到小)
public:
deque<int> que; // 使用deque来实现单调队列
// 每次弹出的时候,比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。
// 同时pop之前判断队列当前是否为空。
void pop(int value) {
if (!que.empty() && value == que.front()) {
que.pop_front();
}
}
// 如果push的数值大于入口元素的数值,那么就将队列后端的数值弹出,直到push的数值小于等于队列入口元素的数值为止。
// 这样就保持了队列里的数值是单调从大到小的了。
void push(int value) {
while (!que.empty() && value > que.back()) {
que.pop_back();
}
que.push_back(value);
}
// 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
int front() {
return que.front();
}
};
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
MyQueue que;
vector<int> result;
for (int i = 0; i < k; i++) { // 先将前k的元素放进队列
que.push(nums[i]);
}
result.push_back(que.front()); // result 记录前k的元素的最大值
for (int i = k; i < nums.size(); i++) {
que.pop(nums[i - k]); // 滑动窗口移除最前面元素
que.push(nums[i]); // 滑动窗口前加入最后面的元素
result.push_back(que.front()); // 记录对应的最大值
}
return result;
}
};347.前 K 个高频元素
思路:
用map统计num出现次数,key为num,value为次数
用vector<pair<int,int>>转存map,first为num,second为次数
sort结合lamda表达式对vector排序,按second的降序排序
返回vector的topK元素
vector<int> topKFrequent(vector<int>& nums, int k) {
map<int, int> nums_map; // <num,num出现次数>
vector<int> res;
for(int i = 0; i < nums.size();++i)
{
nums_map[nums[i]]++;
}
vector<pair<int, int>> nums_vec;
for(auto it = nums_map.begin(); it != nums_map.end();++it)
{
nums_vec.push_back(make_pair(it->first, it->second));
}
sort(nums_vec.begin(), nums_vec.end(),[&](pair<int, int>& lhd, pair<int, int>& rhd){
return lhd.second > rhd.second;
});
for(int i = 0; i < k;++i)
{
res.push_back(nums_vec[i].first);
}
return res;
}




















 289
289

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








