代码随想录：贪心算法

455.分发饼干

力扣题目链接

// 思路：贪心算法，尽可能让大饼干满足大胃口
class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        int res = 0;

        if(g.empty() || s.empty()) return res;

        // 先排序，才能按从大到小去找饼干来满足胃口
        sort(g.begin(),g.end());
        sort(s.begin(), s.end());

        // j指向当前大饼干s
        int j = s.size() - 1;

        // i指向当前大胃口个g，遍历胃口g找到对应的能满足的饼干
        for(int i = g.size() - 1; i >= 0; i--)
        {
            // 当前饼干满足不了胃口，跳到下一个小胃口
            if(j > 0 && s[j] < g[i]) continue;

            // 找到能满足胃口的饼干
            if(j >= 0) res++;

            // 指向下一个饼干
            j--;
        }

        return res;
    }
};


// 思路2：贪心算法，尽可能让小饼干满足小胃口
class Solution {
public:

    int findContentChildren(vector<int>& g, vector<int>& s) {
        int res = 0;

        if(g.empty() || s.empty()) return res;

        // 先排序，才能按从小到大去找饼干来满足胃口
        sort(g.begin(),g.end());
        sort(s.begin(), s.end());

        // j指向当前小饼干s
        int j = 0;

        // i指向当前小胃口g，遍历胃口g找到对应的能满足的饼干
        for(int i = 0; i <  g.size(); i++)
        {
            // 当前饼干满足不了胃口，一直向大饼干方向找到能满足胃口的饼干
            while(j < s.size() && s[j] < g[i]) j++;

            // 找到能满足胃口的饼干
            if(j < s.size()) res++;

            // 指向下一个饼干
            j++;
        }

        return res;
    }
};

376. 摆动序列

力扣题目链接

思路：

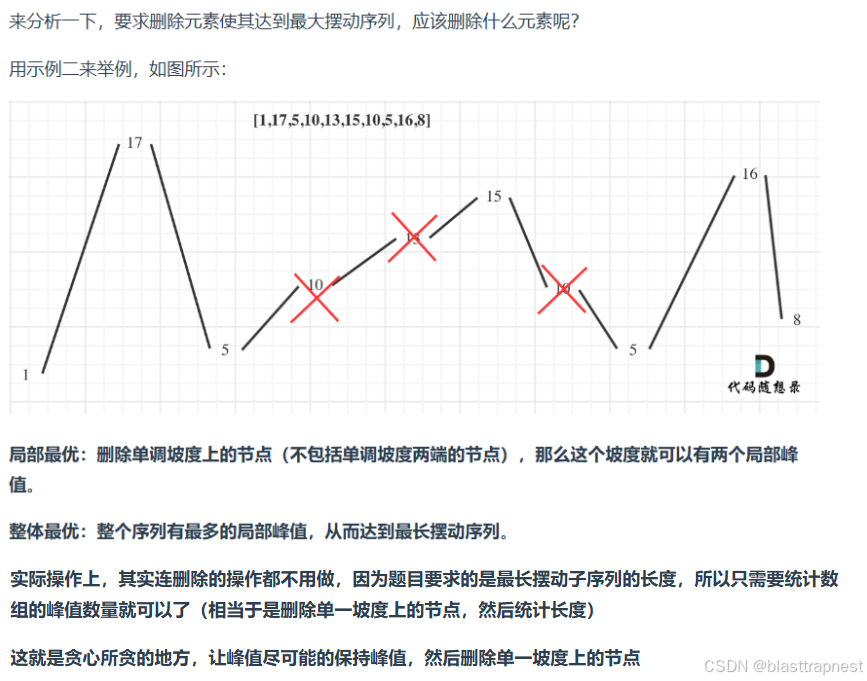
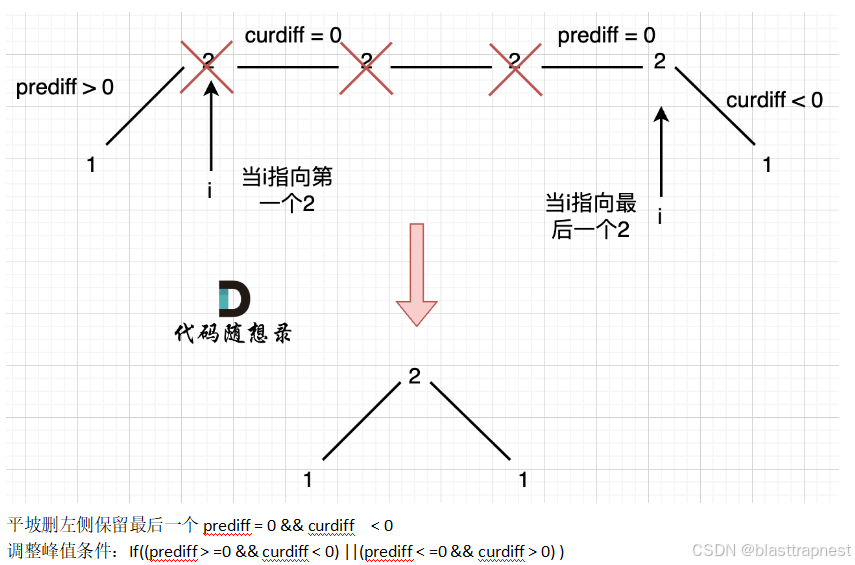
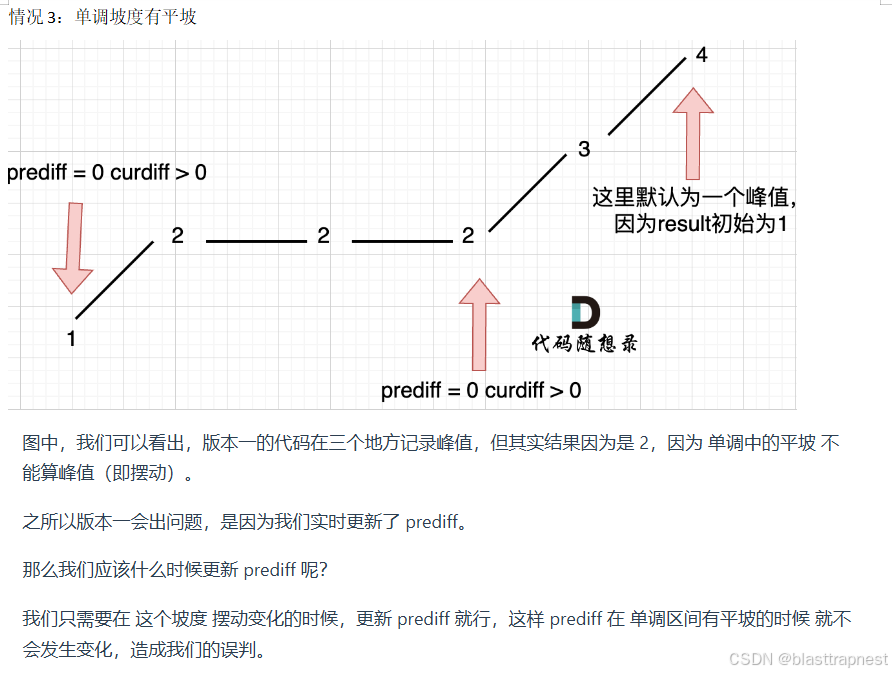
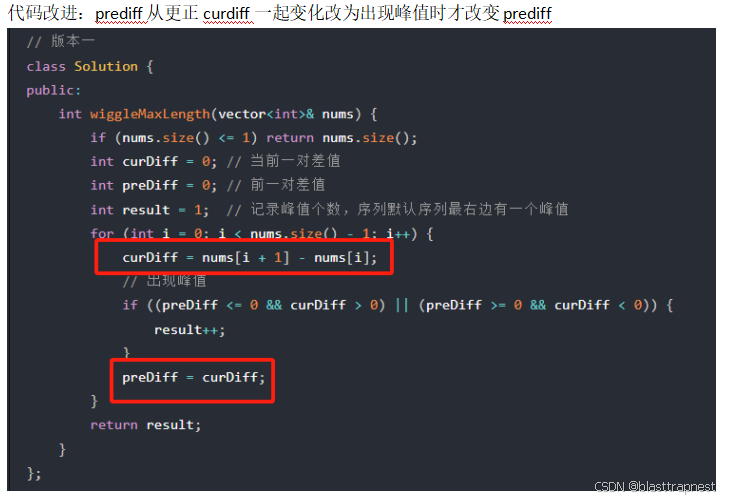
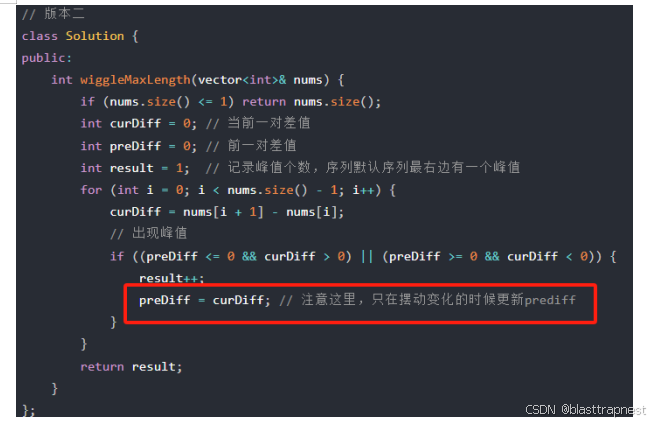
代码：

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        // 特殊考虑单点或空集
        if(nums.size() <= 1) return nums.size();

        // res记录峰值数量，这里默认首处有一个峰值
        // 这样可以视为在首元素之前有一个和首元素相同的元素
        // 如果nums只有2个数, 扩充后变为3个元素可和后面的算法统一规则
        // 两数不等是平升或者平降，res = 2, 两数相等是平平，res = 1
        int res = 1;

        int prediff = 0; // 默认在首元素之前有一个和首元素相同的元素，所以prediff为0
        int curdiff = 0;

        // res默认首元素前有一个相同值，i可以从0开始，直到最后一个值的前一个元素
        for(int i = 0; i + 1 < nums.size(); ++i)
        {
            // 注意这里不能rediff = nums[i] - nums[i - 1]
            // 因为前面的点可能在坡上，不考虑为峰值点
            // prediff只记录确保是峰值的两点差
            curdiff = nums[i + 1] - nums[i];

            // prediff和curdiff异号时是峰值点
            // 这里prediff考虑等于0：平台期后上升或者下降的拐点也是峰值
            if((prediff <= 0 && curdiff > 0) || (prediff >= 0 && curdiff < 0))
            {
                res++;
                // 出现了峰值，更新prediff
                prediff = curdiff;
            }                  
        }
        return res;
    }
};

53. 最大子序和

力扣题目链接

思路：

当前连续和+nums[i]，如果连续和为负只会拖累nums[i]变小，不如选择从nums[i]重新开始遍历

局部最优：求到连续和为负，就选下一个数为起点

代码：

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        // 注意nums可能只有一个负元素，所以res要设置的足够小
        int res = INT32_MIN;

        // 记录从i开始的序列和
        int count = 0; 

        for(int i = 0; i < nums.size(); ++i)
        {
            count += nums[i];

            // 如果当前序列和比结果大则更新res
            res =count > res ? count: res;

            // 当前序列和小于0，重新把下一个位置记录为序列和的开始
            // count归0，res不能归0，res记录的是之前扫描过的最大和
            if(count <= 0)  count = 0;
        }

        return res;
    }
};

122.买卖股票的最佳时机 II

力扣题目链接

代码：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int res = 0;
        for(int i = 1; i < prices.size(); ++i)
        {
            int day_profit = prices[i] - prices[i - 1];
            if(day_profit > 0) res += day_profit;
        }

        return res;
    }
};

55. 跳跃游戏

力扣题目链接

思路：

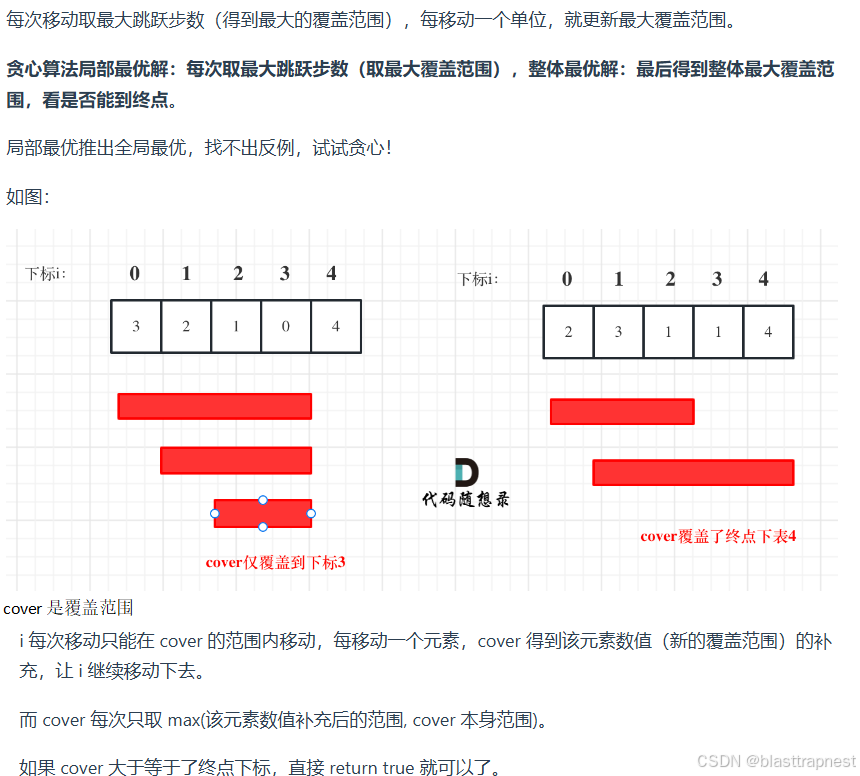
    bool canJump(vector<int>& nums) {
        if(nums.size() <= 1) return true;

        int cover = 0; // 定义覆盖范围

        // i在cover范围内遍历
        for(int i = 0; i <= cover; ++i)
        {
            // 取i位置的步数nums[i]扩充范围
            cover = max(cover, i + nums[i]);

            // 扩充后的范围覆盖了最后的点, 说明可以跳到最后
            if(cover >= nums.size() - 1) return true;
        }

        // 遍历完了cover范围，没有return true说明走不到最后
        return false;
    }