修理牧场问题--Python

一、问题引入

农夫要修理牧场的一段栅栏，他测量了栅栏，发现需要 n 块木头，每块木头长度为整数 li个长度单位，于是他购买了一条很长的、能锯成 n 块的木头，即该木头的长度是 li的总和。

但是农夫自己没有锯子，请人锯木的酬金跟这段木头的长度成正比。为简单起见，不妨就设酬金等于所锯木头的长度。例如，要将长度为 20 的木头锯成长度为 8、7 和 5 的三段，第一次锯木头花费 20，将木头锯成 12 和 8；第二次锯木头花费 12，将长度为 12 的木头锯成 7 和 5，总花费为 32。如果第一次将木头锯成 15 和 5，则第二次锯木头花费 15，总花费为 35（大于 32）。

请编写程序帮助农夫计算将木头锯成 n 块的最少花费。

输入格式:
输入首先给出正整数 n（≤10^4），表示要将木头锯成 n 块。第二行给出 n 个正整数（≤50），表示每段木块的长度。

输出格式:
输出一个整数，即将木头锯成n块的最少花费。

输入样例:

8
4 5 1 2 1 3 1 1

输出样例:

49

二、解题思路

1.流程图

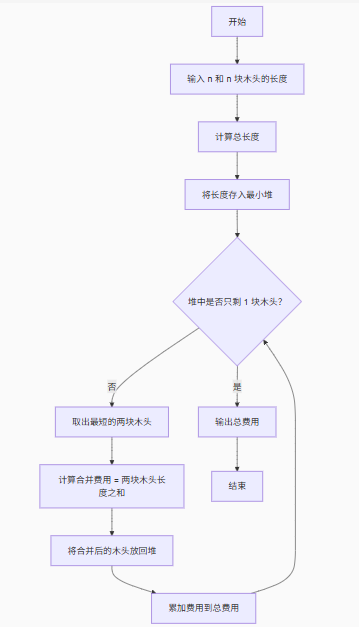
2.解题步骤

1. 计算总长度：首先计算所有小木头的总长度，即初始木头的长度。
2. 优先队列（最小堆）：将所有木头的长度存入最小堆，方便快速获取最短的两块木头。
3. 合并木头：
   ◦ 每次从堆中取出最短的两块木头，合并它们（相当于锯木操作）。
   ◦ 合并费用 = 这两块木头的长度之和。
   ◦ 将合并后的新木头长度放回堆中。
4. 累加费用：每次合并的费用累加到总费用中。
5. 终止条件：当堆中只剩一块木头时，停止合并，输出总费用。

三、代码实现

import heapq

def min_cutting_cost(n, lengths):
    heapq.heapify(lengths)  # 转为最小堆
    total_cost = 0
    while len(lengths) > 1:
        # 取出最短的两块木头
        first = heapq.heappop(lengths)
        second = heapq.heappop(lengths)
        cost = first + second
        total_cost += cost
        # 将合并后的木头放回堆
        heapq.heappush(lengths, cost)
    return total_cost

n = int(input())
lengths = list(map(int, input().split()))
print(min_cutting_cost(n, lengths))

复杂度分析：

时间复杂度：O(n log n)，因为每次堆操作（heappop 和 heappush）的时间复杂度是 O(log n)，总共需要进行 n-1 次合并。

空间复杂度：O(n)，用于存储堆。

四、个人总结

通过本次实验，我深刻理解了如何利用优先队列（最小堆）来高效解决最优合并问题。最初面对题目时，我误以为应该像切木棒问题那样从最大段开始分割，但在模拟计算过程中发现这种策略会导致总费用偏高。

通过反复尝试和分析示例数据，我意识到这个问题本质上与哈夫曼编码的构建过程高度相似，关键在于每次都要选择当前最小的两个元素进行合并。在实现过程中，我学会了如何正确使用Python的heapq模块来维护最小堆结构，特别是掌握了heappop和heappush这两个关键操作的实际应用。

调试阶段遇到的一个典型错误是忘记将合并后的新长度重新放入堆中，导致后续计算出错，这个教训让我更加注重算法流程的完整性。这次实验不仅让我掌握了优先队列解决特定问题的技巧，更重要的是培养了我将实际问题抽象为数学模型的能力，以及通过具体案例验证算法正确性的思维习惯。