张量展开和Tensorly使用

首先介绍一下张量的切片



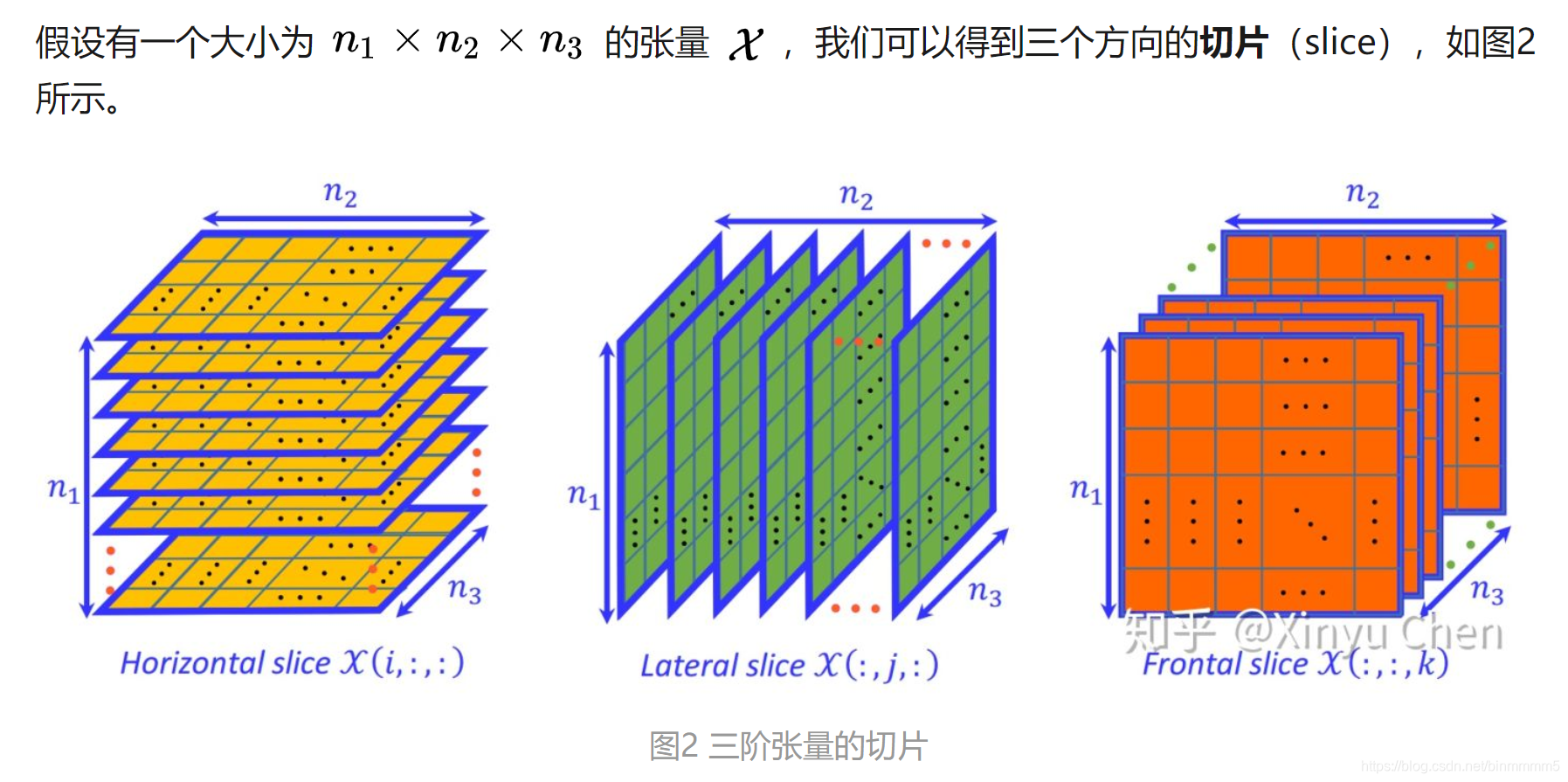
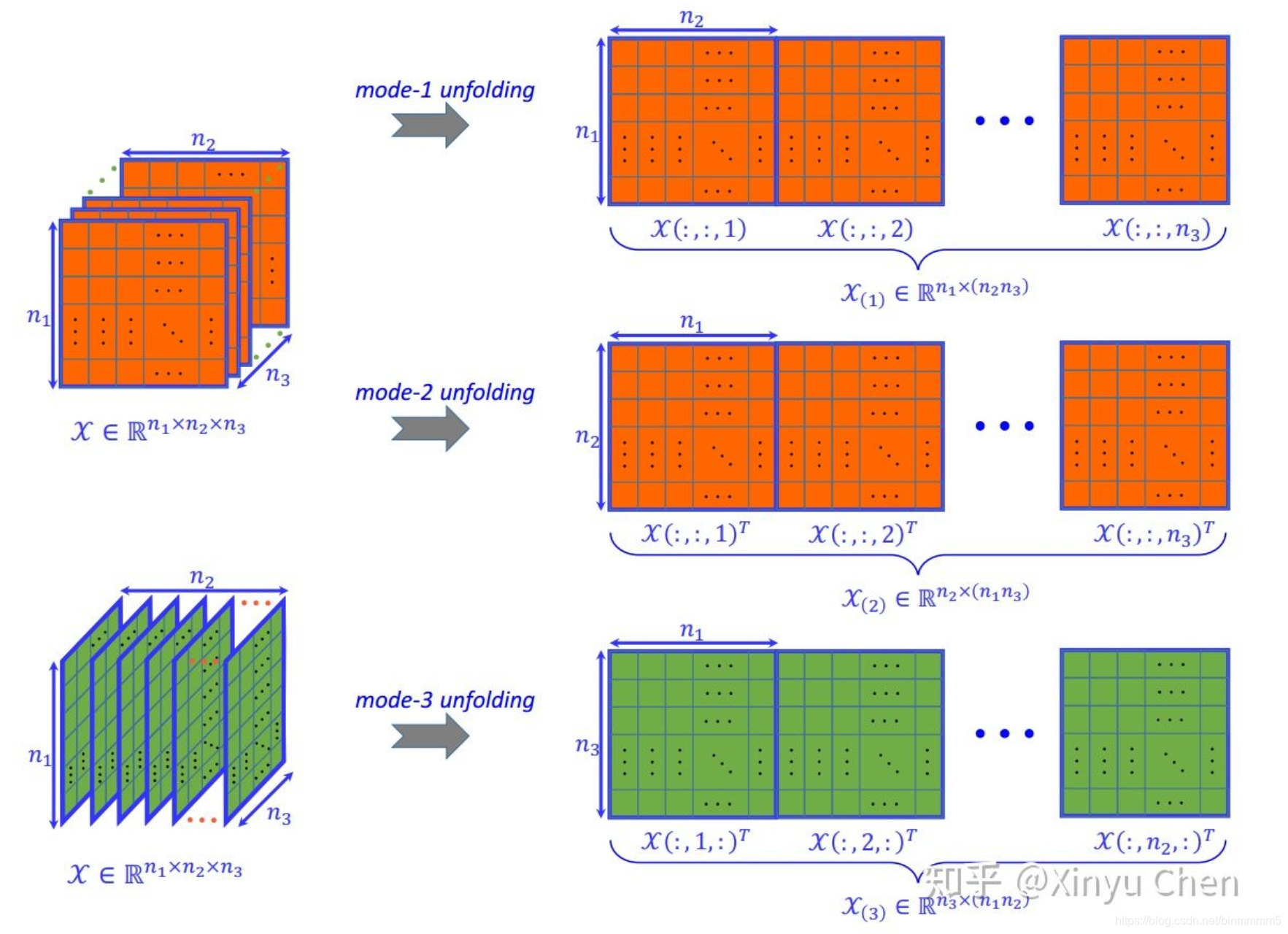
例子：https://zhuanlan.zhihu.com/p/24824550

从例子中感觉这么展开就是为了满足：三阶张量为X是n1×n2×n3阶的，如果按mode-2展开，矩阵就是n2×(n1×n3)的，具体为什么要这么转置，这个还需要思考，而且还有更高阶的怎么推到展开也需要思考。说一个实际的问题，我发现在Tensorly里面除了好象展开的方法和这个说的不太一样，不过最后得到的展开维度是一样的(别问我，我也不知道为啥)···············

下面给一些自己尝试使用Tensorly库的代码：

import numpy as np
import tensorly as tl
from tensorly.tenalg import *

#下面这是kronecker积，注意要把两个tensor放在一个list里面
arr1 = tl.tensor(np.array([[1,2],[3,4]]))
arr2 = tl.tensor(np.array([[5,6,7],[8,9,10]]))
arr3 = [arr1,arr2]
arr4 = kronecker(arr3)
print(arr4)

#内积的inner函数我总是报错，但是下面这个方法和内积效果是一样的
arr5 = tl.tensor(np.arange(12).astype(np.float64).reshape(3,2,2))
arr6 = tl.tensor(np.arange(12).astype(np.float64).reshape(3,2,2))
print(arr5)
print(arr5*arr6)
print(tl.sum(arr5*arr6))

#下面这是一个2*2*2*2的四阶张量，我觉得这玩应如果不用reshape定义就得这么一层一层写，不然能写懵了，注意在numpy里维度的顺序，可以看看三维的就懂了
arr = tl.tensor(np.array([
    [
        [[1,2],[3,4]],
        [[5,6],[7,8]]
    ],
    [
        [[9,10],[11,12]],
        [[13,14],[15,16]]
    ]
]))

#接下来就是按mode展开，，注意第一个mode是0，而不是1
arr = tl.tensor(np.arange(2*4*3).reshape(3,4,2))
print(arr)
print(tl.unfold(arr, mode=0))
print(tl.unfold(arr, mode=1))
print(tl.unfold(arr, mode=2))
M1 = tl.tensor(np.arange(20).reshape(5, 4))
M2 = tl.tensor(np.arange(18).reshape(6, 3))
M3 = tl.tensor(np.arange(14).reshape(7, 2))

#首先是张量和矩阵的模态积
result1 = mode_dot(arr,M1,1)
print(result1)
print(tl.shape(result1))
M_list = [M1,M2,M3]
mode_list = [1,0,2]

#一个张量和多个矩阵的模态积，注意把矩阵们放在list里，然后把每个矩阵对应的mode放在另一个list里
result2 = multi_mode_dot(arr,M_list,mode_list)
print(result2)
print(tl.shape(result2))

关于CP分解部分已经在之前的介绍过了，不过这个CP分解还是可以还原的（不过这个函数具体我自己并没尝试，可以以后试试）

下面尝试一下tucker分解：

X = tl.tensor(np.arange(24).astype(np.float64).reshape(3, 4, 2))
print(X)
#rank中的list也是core的维度
core, factors = tucker(X, rank=[2, 2, 2])
print(core)
print(core.shape)
f1,f2,f3 = factors
print(f1.shape)
print(f2.shape)
print(f3.shape)
#根据性质把分解出来的核张量和矩阵还原回去
result = multi_mode_dot(core,factors,[0,1,2])
np.set_printoptions(suppress=True)
print(result)

下面展示一下输出的结果：
X:
[[[ 0. 1.]
[ 2. 3.]
[ 4. 5.]
[ 6. 7.]]

[[ 8. 9.]
[10. 11.]
[12. 13.]
[14. 15.]]

[[16. 17.]
[18. 19.]
[20. 21.]
[22. 23.]]]
core和他的shape：

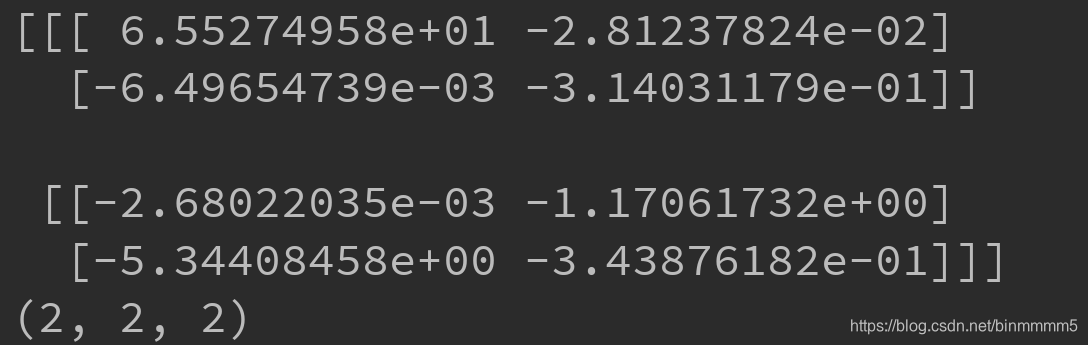
f1,f2,f3:

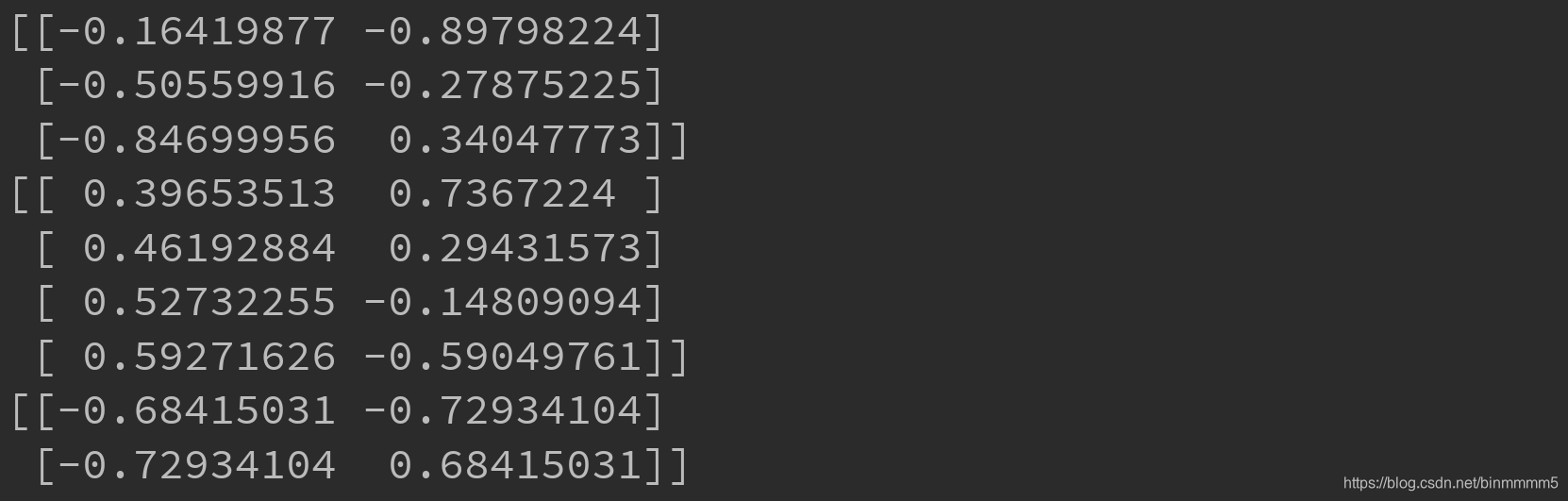
还原回来的result：
[[[ 0. 1.]
[ 2. 3.]
[ 4. 5.]
[ 6. 7.]]

[[ 8. 9.]
[10. 11.]
[12. 13.]
[14. 15.]]

[[16. 17.]
[18. 19.]
[20. 21.]
[22. 23.]]]

发现是一样的，基础部分完结撒花