B. Omkar and Last Class of Math【1300 / 数论】

寻找最大差值因子对

最新推荐文章于 2025-02-18 19:52:26 发布

原创最新推荐文章于 2025-02-18 19:52:26 发布 · 163 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#c++

数论专栏收录该内容

34 篇文章

订阅专栏

该博客主要讨论了一个编程问题，即找到一个整数n的所有因子对(a, b)，使得a+b=n，并最大化a和b之间的最大公约数。通过遍历因子i并计算n/i，博主找到了一种优化方法，始终更新最小的b值，从而得到最大公倍数为最大值的因子对。代码实现使用了C++，并在Codeforces平台上提出。

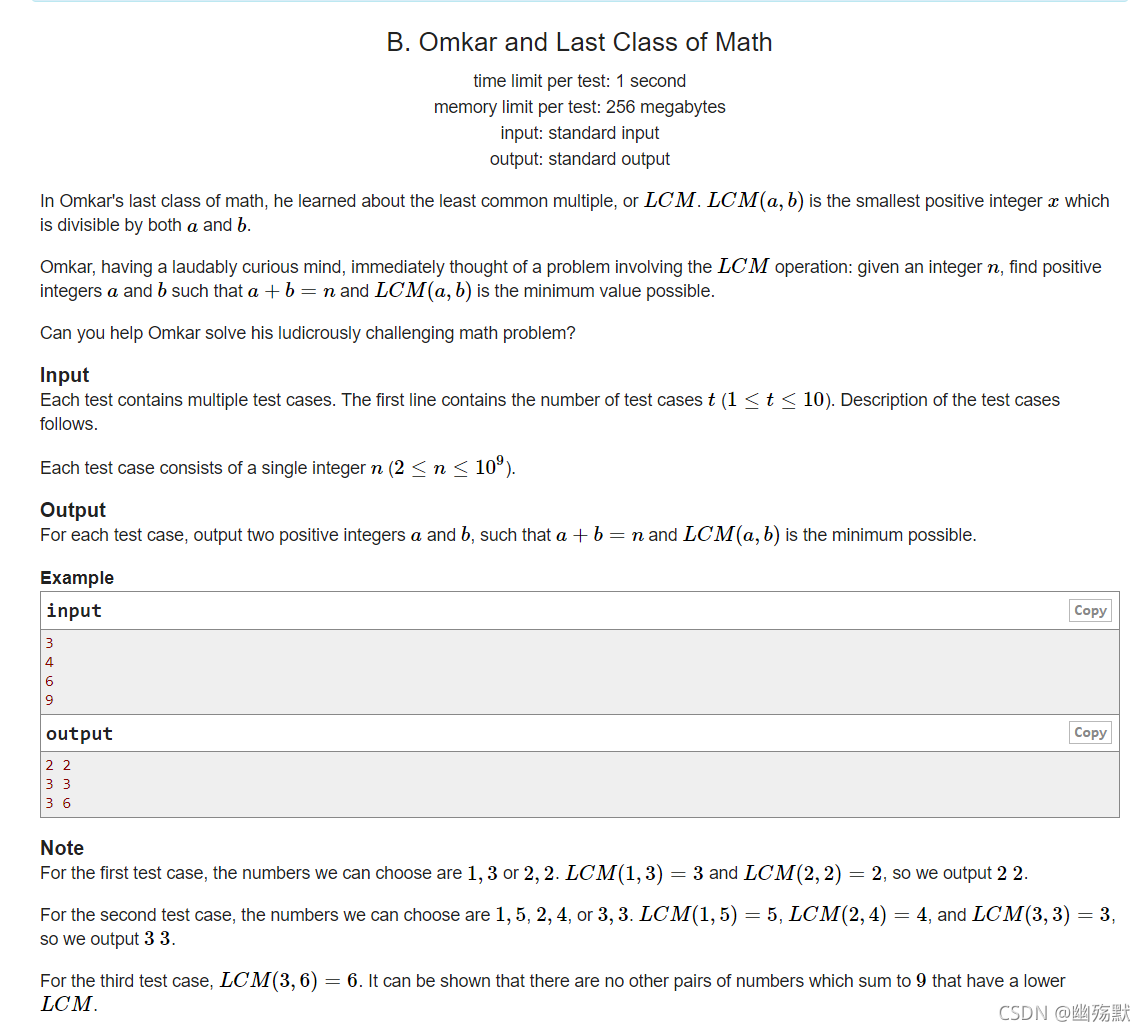
在这里插入图片描述
https://codeforces.com/problemset/problem/1372/B
设x是n的因子，a=x，b=n-x,那么就有max(a,b)%min(a,b)=0
那么a，b的最大公倍数便是max(a,b)
例如: 8=2*4 那么可以分成 4 4
例如: 16=4*4 那么可以分成 4 12 必可以是它的约数
随着约数的增大，我们的分的第二份越来越小，越来越是正解。

#include<bits/stdc++.h>
using namespace std;
int main(void)
{
	int t; cin>>t;
	while(t--)
	{
		int n; cin>>n;
		int cnt=n,x=1,y=n-x;
		for(int i=2;i<=n/i;i++)
		{
			if(n%i==0)
			{
				int temp1=n/i,temp2=n-temp1;//总共i份 1份给temp1 (i-1)份给temp2
				if(temp2<=cnt) cnt=temp2,x=temp1,y=temp2;
			}
		}
		cout<<x<<" "<<y<<endl;
	}
	return 0;
}