机器学习与深度学习09-支持向量机01-优快云博客

前文回顾

上一篇文章链接：地址

1.什么是支持向量机

什么是支持向量机（SVM）？它主要用于解决什么类型的问题？
支持向量机（Support Vector Machine, SVM）是一种强大的监督学习算法，主要用于分类和回归问题。SVM的核心思想是寻找一个最优的超平面或决策边界，以最大化不同类别数据点之间的间隔，并尽量避免误分类
线性SVM（Linear SVM）
考虑一个二元分类问题，其中我们有一个训练数据集，每个数据点都有一组特征 (X) 和一个标签 (y)，其中 (y) 可以是1或 -1（或任何两个不同的类别）。我们的目标是找到一个超平面，可以表示为：
$w\cdot x + b = 0$
其中，(w) 是法向量（权重向量），(b) 是截距，(x) 是输入特征向量。超平面将特征空间分为两个区域，一个表示正类别，另一个表示负类别
支持向量（Support Vectors）
支持向量是训练数据中距离超平面最近的数据点。它们是用于定义分类间隔（Margin）的关键元素。分类间隔是指超平面与最近的支持向量之间的距离
最大化间隔（Maximizing Margin）
SVM的关键目标是找到一个超平面，使得分类间隔最大化。分类间隔的计算如下：
$Margin=\frac{2}{\|w\|}$
其中，(|w|) 表示权重向量 (w) 的范数
SVM的优化问题
线性SVM的优化问题可以形式化为以下凸优化问题。最小化目标函数:
$\frac{1}{2}\|w\|^{2}$
在满足以下约束条件的情况下:
$\begin{align*} y_{i}(w\cdot x_{i}+b)&\geq1，\text{ 对于所有样本 }i\\ y_{i}&\in\{ -1,1\}，\text{ 样本标签} \end{align*}$
这个优化问题的目标是最小化权重向量 (w) 的范数，以最大化分类间隔，同时确保所有样本都位于分类间隔以外
核函数（Kernel Function）：
SVM 也可以应用于非线性分类问题，通过引入核函数来将数据映射到高维特征空间，从而在高维空间中找到线性可分的超平面。常见的核函数包括线性核、多项式核和径向基函数（RBF）核

2.支持向量机的基本原理

支持向量机（SVM）的基本原理是在特征空间中找到一个超平面（或决策边界），该超平面可以最大化不同类别数据点之间的间隔，同时尽量避免误分类，SVM的工作原理在分类和回归任务中有所不同：
在分类任务中，

SVM的目标是找到一个超平面，将数据点分为两个不同的类别，使得分类间隔（Margin）最大化
Margin是指超平面与最近的支持向量之间的距离，即两个平行超平面之间的距离
支持向量是离超平面最近的数据点，它们对定义分类间隔非常重要
SVM分类器尝试最小化目标函数，该函数包括最小化权重向量的范数以及使每个数据点都位于正确的一侧（根据类别标签）的约束条件
对于非线性数据，可以使用核函数来将数据映射到高维空间，以使数据在高维空间中线性可分

在回归任务中

SVM回归的目标是找到一个超平面，使得数据点尽量接近超平面，同时在一定容忍度内
在回归问题中，SVM的目标是最小化一个损失函数，损失函数衡量了数据点离超平面的距离以及容忍度的违规情况
容忍度（Tolerance）是一个控制在训练期间允许数据点距离超平面的程度的参数

3.什么是超平面

SVM中的超平面是一个数学概念，它是用于分割特征空间以执行二元分类的关键元素。超平面是一个维数比特征空间低一的线性子空间。在二元分类问题中，SVM的目标是找到一个超平面，可以将数据点分为两个不同的类别，并且在最大程度上使分类间隔（Margin）最大化,以下是超平面的概念和用于二元分类的决策过程：

超平面的定义：对于一个(d)维特征空间，一个超平面可以表示为：
$w\cdot x + b = 0$
其中，(w) 是法向量（权重向量）的权重，(b) 是超平面的偏移（截距），(x) 是(d)维输入特征向量。超平面将特征空间分为两个部分，一个表示正类别，另一个表示负类别

SVM的决策规则：在二元分类中，SVM的决策规则基于超平面上的点(w\cdot x + b) 的符号：

如果 $w\cdot x + b>0$ ，则数据点(x)被分类为正类别（标签为 +1）
如果 $w\cdot x + b<0$ ，则数据点(x)被分类为负类别（标签为 -1）

最大化间隔：SVM的目标是选择一个超平面，以最大化分类间隔（Margin）。分类间隔是指超平面与最近的训练样本点之间的距离。最大化分类间隔可以增加模型的鲁棒性，使其对新数据的泛化性能更好

4.软间隔和硬间隔SVM

软间隔和硬间隔SVM是SVM模型的两种变体，它们的主要区别在于对数据的容忍度和对异常点的处理

硬间隔SVM

硬间隔SVM旨在找到一个完全将训练数据分开的超平面，其中没有训练数据点位于分类间隔内部。
在硬间隔SVM中，数据点必须严格满足线性可分的条件，这意味着数据必须严格位于正确的一侧，不允许任何分类错误。
硬间隔SVM对异常点非常敏感，即使一个异常点出现在训练数据中，都可能导致无法找到满足条件的超平面。

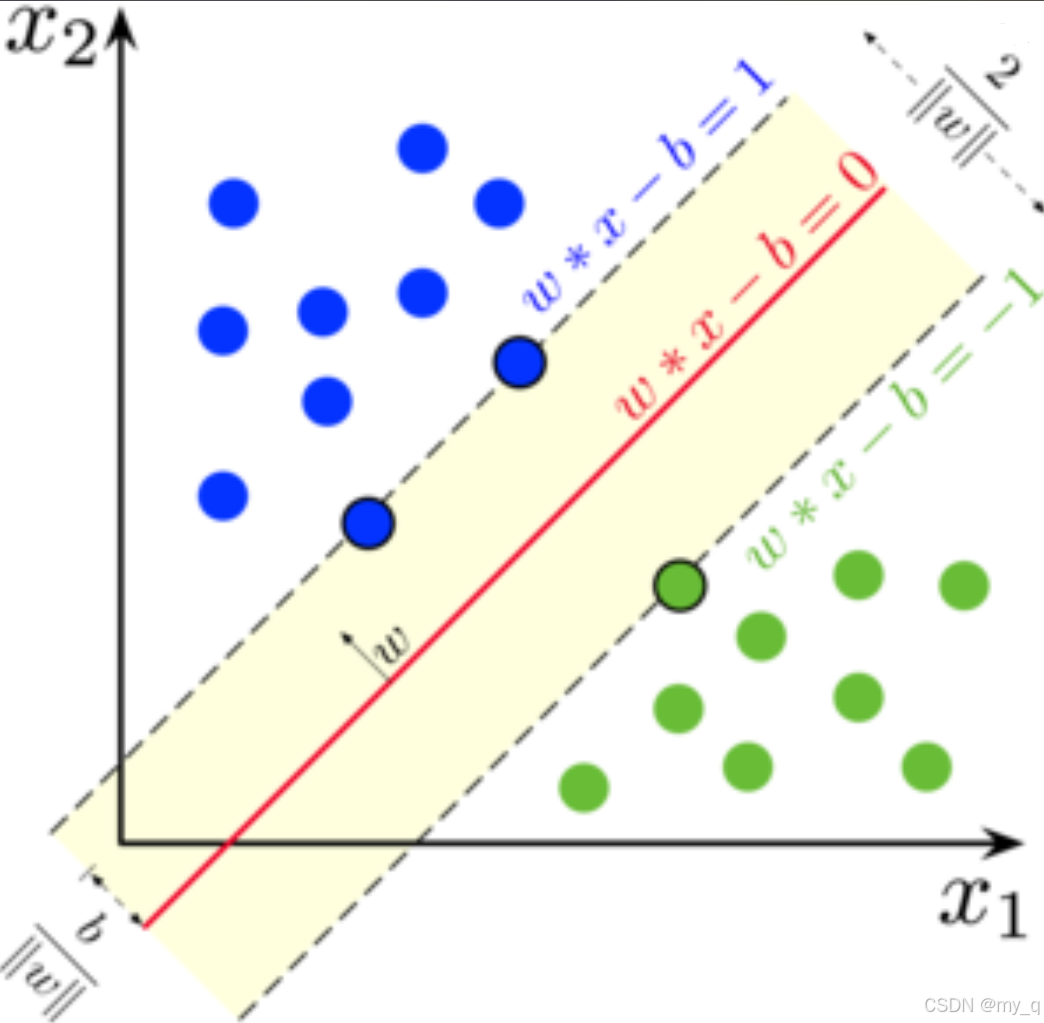
硬间隔SVM的示意图如下，其中红色和蓝色点表示不同类别的数据，绿色线表示超平面，它严格分开了两个类别的数据:
在这里插入图片描述

软间隔SVM

软间隔SVM引入了容忍度（Tolerance）的概念，允许一些数据点位于分类间隔内部或甚至被错误分类，以提高模型的鲁棒性。
软间隔SVM的目标是找到一个超平面，尽量最大化分类间隔，同时限制分类错误或间隔内部的数据点数量。
软间隔SVM更加鲁棒，能够处理一些噪声或异常点，不需要严格满足线性可分条件。

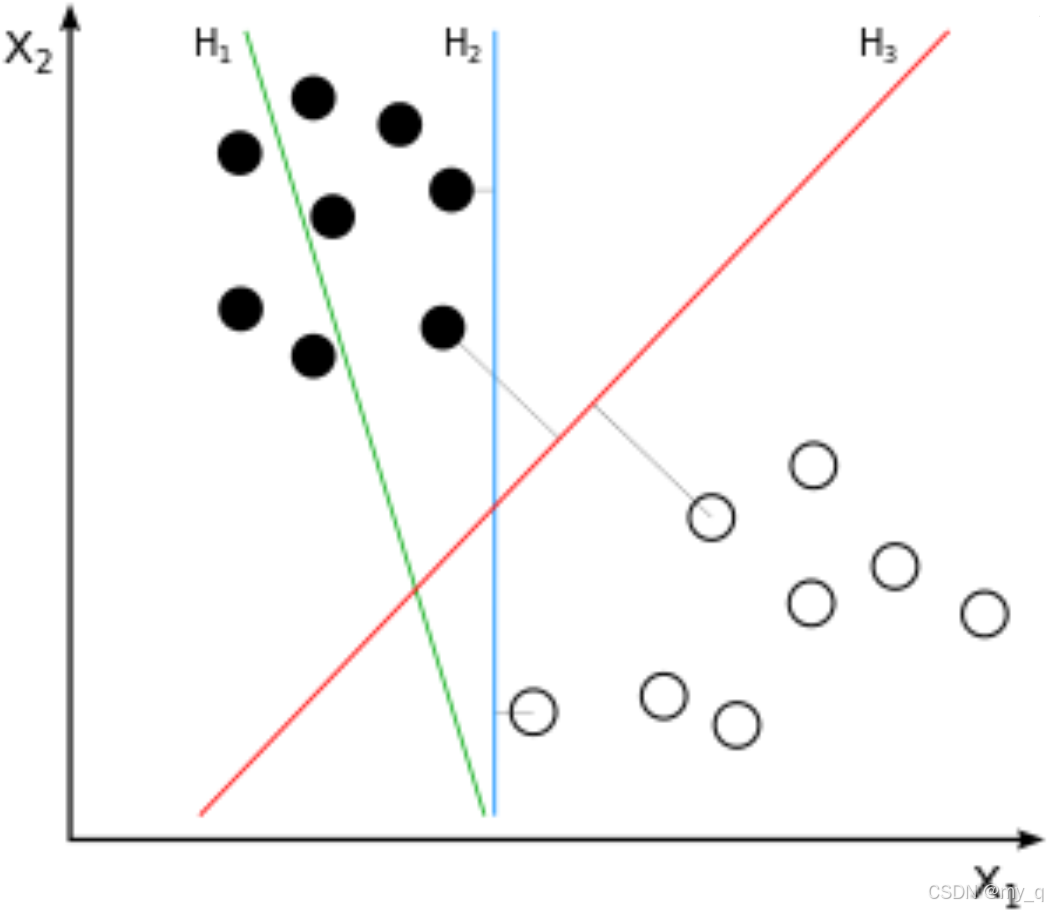
软间隔SVM的示意图如下，其中部分异常点（圆圈）位于分类间隔内部，但模型仍然能够找到一个满足条件的超平面:
在这里插入图片描述应用场景：

硬间隔SVM：适用于数据集严格线性可分的情况，当我们有信心数据不包含异常点或噪声时
软间隔SVM：更加鲁棒，适用于数据集可能包含一些异常点、噪声或不严格线性可分的情况，允许一定程度的分类错误或数据点位于分类间隔内

通常，软间隔SVM是更实际的选择，因为它在处理现实世界的数据时更加健壮。硬间隔SVM通常在理论研究中用于分析和证明，而在实际应用中，软间隔SVM更常见

5.SVM如何处理非线性数据

在SVM中处理非线性可分的数据时，通常使用核函数（Kernel Function）来将数据映射到一个高维特征空间，使得数据在这个高维空间中变得线性可分

核函数的作用是计算两个数据点之间的相似度或内积，而不需要显式地将数据映射到高维空间。以下是一些常用的核函数及其作用：

线性核函数（Linear Kernel）：这是SVM的默认核函数，它在原始特征空间中计算数据点之间的线性关系。适用于线性可分的数据
多项式核函数（Polynomial Kernel）：多项式核函数通过引入多项式项将数据映射到高维空间，使其变得更容易分离。它有一个参数d，表示多项式的阶数
高斯径向基核函数（Gaussian Radial Basis Function Kernel）：高斯核函数通过计算数据点之间的相似度来将数据映射到无限维的高维空间。它有一个参数σ，控制了特征映射的“宽度”
Sigmoid核函数（Sigmoid Kernel）：Sigmoid核函数将数据映射到高维空间，类似于神经网络的激活函数。它在某些特定应用中有用，但不如高斯核函数和多项式核函数常用

下面是一个示意图，说明如何使用核函数处理非线性可分的数据：
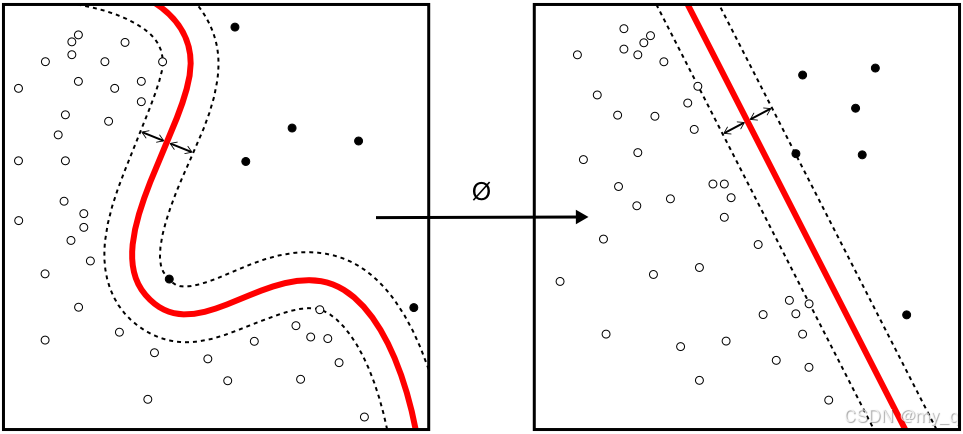
在这里插入图片描述
在这个图中，左侧是原始特征空间中的数据点，它们不能被单个超平面分开。右侧是使用核函数将数据映射到高维空间后的结果。在高维空间中，数据点变得线性可分，可以找到一个超平面（这里是一条直线）来分隔它们，这个示意图展示了核函数如何改变数据的表示，使得原本在低维度中难以处理的非线性可分问题变得容易处理。核函数的选择通常取决于数据的性质和具体问题，需要根据实际情况进行调优