机器学习笔记 KAN网络架构简述（Kolmogorov-Arnold Networks）

最新推荐文章于 2025-05-08 07:18:53 发布
最新推荐文章于 2025-05-08 07:18:53 发布
阅读量1.1k 收藏 1
点赞数
CC 4.0 BY-SA版权
分类专栏： 深度学习从入门到精通 文章标签： 机器学习 人工智能 KAN网络架构 神经网络 函数逼近
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/bashendixie5/article/details/138909375
本文介绍了KAN（Kolmogorov-Arnold Networks），一种受柯尔莫哥洛夫-阿诺德表示定理启发的神经网络架构。不同于传统的多层感知器，KAN使用可学习的一维样条函数替代固定激活函数和线性权重，增强了函数逼近能力。样条曲线的灵活性使得KAN能够更好地适应高维数据，减少了线性权重带来的限制。尽管KAN在某些场景下可能面临过度拟合和计算资源需求的问题，但其在科学和工程任务中的表现展示了其潜力。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

一、简述

        在最近的研究中，出现了号称传统多层感知器 (MLP) 的突破性替代方案，重塑了人工神经网络 (ANN) 的格局。这种创新架构被称为柯尔莫哥洛夫-阿诺德网络 (KAN)，它提出了一种受柯尔莫哥洛夫-阿诺德表示定理启发的函数逼近的方法。

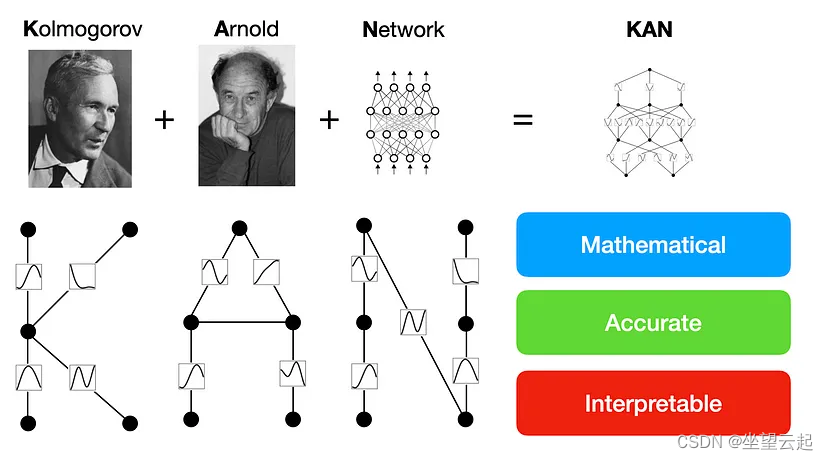
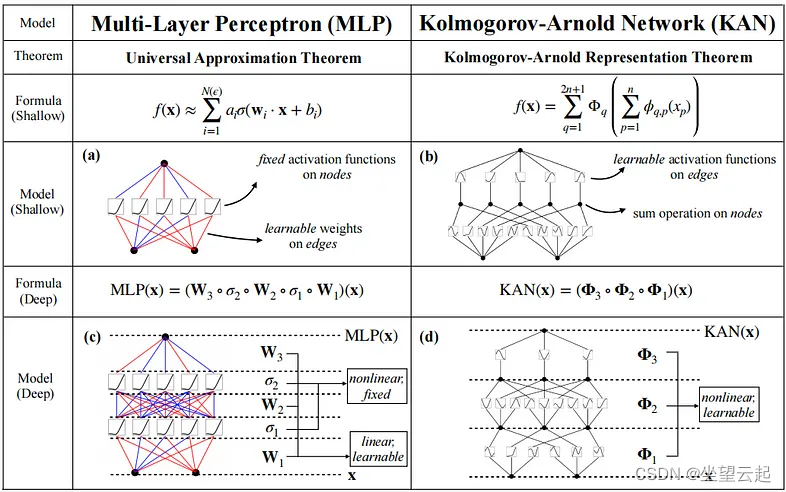
        与 MLP 不同，MLP 依赖于各个节点的固定激活函数，KAN 引入了边缘上的可学习激活函数，从根本上改变了神经网络的结构。这种独特的设计功能完全消除了线性权重矩阵，代之以可学习的一维样条函数。就是说KAN根本没有线性权重，每个权重参数都被参数化为样条函数的单变量函数所取代。

二、Kolmogorov–Arnold表示定理

        该理论基于多元连续函数的概念。根据该理论，任何多元连续函数f都可以写成单个变量的连续函数的有限组合相加等（

了解本专栏 订阅专栏 解锁全文
KAN网络：一种新型神经网络架构的介绍与实现
qq_53298558的博客
05-11 7139
使用KAN网络进行简单的数学建模与预测
KAN网络架构浅析
sheex2012的博客
06-04 5851
与 MLP 类似，KAN 实际上也具有全连接结构，区别在于，MLPs在节点（神经元）上放置固定的激活函数，而 KAN在边缘（权重）上放置的是可学习的激活函数。，与原始传统的MLP相比，特别是现代MLP采用了更为简单的RELU取代Sigmod激活函数，有效解决了梯度爆炸或消失问题，从而大大降低了深度网络构建和训练难度（当然，还得有Resnet加持）。3. KAN在不同类型的任务和数据集上的泛化能力还需要进一步验证，github上已经有很多关于KAN的实验，不同的研究者的实验结果并不一致。
【Pytorch】基于LSTM-KAN、BiLSTM-KAN、GRU-KAN、TCN-KAN、Transformer-KAN(各种KAN修改一行代码搞定)的共享单车租赁预测研究(数据可换)
qq_72962865的博客
05-08 783
共享单车作为现代城市交通的重要组成部分，其租赁量的准确预测对于优化资源配置、提升运营效率以及缓解城市交通拥堵具有至关重要的意义。传统的预测模型，如ARIMA、LSTM、GRU等，在处理复杂的时序数据时往往面临信息遗忘或捕捉长期依赖不足的问题。近年来，以Transformer为代表的注意力机制模型在处理长序列数据方面展现出强大的能力，但其计算复杂度较高。而新近提出的Kolmogorov-Arnold Networks (KANs) 以其理论上的通用逼近能力和潜在的生物可解释性受到关注。
探秘KAN：Kolmogorov-Arnold网络，深度学习新星！
gitblog_00060的博客
05-26 841
探秘KAN：Kolmogorov-Arnold网络，深度学习新星！ 去发现同类优质开源项目:https://gitcode.com/ 在人工智能和机器学习领域，创新从未止步。最近，一个名为Kolmogorov-Arnold网络（KAN）的新概念引起了广泛的关注。KAN是一种基于Kolmogorov-Arnold表示定理的神经网络模型，它的独特之处在于将可学习的激活函数应用到边（权重），而非传统的节...
KAN: Kolmogorov–Arnold Networks
qq_22583741的博客
05-28 1685
受柯尔莫戈罗夫-阿诺德表示定理的启发，我们提出了柯尔莫戈罗夫-阿诺德网络（KANs），作为多层感知器（MLPs）的有前途的替代方案。与 MLPs 的节点（“神经元”）上具有固定的激活函数不同，KANs 的边（“权重”）上具有可学习的激活函数。KANs 完全没有线性权重——每个权重参数都被一个参数化为样条的单变量函数所取代。我们展示了这个看似简单的改变使得 KANs 在准确性和可解释性方面优于 MLPs。
KAN：Kolmogorov–Arnold Networks
通街是密人有的博客
05-06 4010
受Kolmogorov-Arnold表示定理的启发，我们提出Kolmogorov-Arnold网络(KAN)作为多层感知器(MLP)的有前途的替代品。MLP在节点(“神经元”)上有固定的激活函数，而KAN在边缘(“权重”)上有可学习的激活函数。kan根本没有线性权重——每个权重参数都被参数化为样条的单变量函数所取代。我们表明，这个看似简单的改变使得KAN在准确性和可解释性方面优于MLP。就准确性而言，在数据拟合和PDE求解方面，更小的KAN可以达到与更大的MLP相当或更好的准确性。
Kolmogorov-Arnold Network (KAN) 的高效Pytorch实现
05-06
Kolmogorov-Arnold Network (KAN) 的高效Pytorch实现 原始实现的性能问题主要是因为它需要扩展所有中间变量来执行不同的激活函数。 对于具有输入和输出的层，原始实现需要将输入扩展为具有形状的张量来执行激活函数...
KAN网络（Kolmogorov-Arnold Network）一种新型的神经网络架构
06-06
KANs的数学理论基础来自于Kolmogorov-Arnold表示定理。该定理表明每个多元连续函数都可以表示为单变量连续函数的两层嵌套叠加。在KAN网络中，这种结构通过可学习的单变量函数和加法运算来实现。 学习过程 MLP的边是...
改进KAN模型Pytorch完整源码，Kolmogorov-Arnold Networks
07-25
改进KAN模型Pytorch完整源码，Kolmogorov-Arnold Networks Kolmogorov-Arnold Networks (KAN) 使用 Chebyshev polynomials 替换 B-splines. class MNISTChebyKAN(nn.Module): def __init__(self): super...
KAN模型Pytorch源码优化，Kolmogorov-Arnold Networks实现
最新发布
07-15
改进KAN模型的Pytorch完整源码，Kolmogorov-Arnold Networks (KAN) 使用 Chebyshev polynomials 替换 B-splines。class MNISTChebyKAN(nn.Module): def __init__(self): super(MNISTChebyKAN, self).__init__() self...
全新神经网络架构KAN——本文用于学习与探索
xiao_ling_yun的博客
05-11 1万+
24年新神经网络结构KAN论文学习 + 解析，KAN有望作为MLP的更优平替
【Kolmogorov-Arnold网络 替代多层感知机MLPs】KAN: Kolmogorov-Arnold Networks
Arachis_X的博客
05-08 1764
受Kolmogorov-Arnold 表示定理的启发，我们提出了Kolmogorov-Arnold网络（KANs）作为多层感知器（MLPs）的替代品。MLP 在节点（“神经元”）上有固定的激活函数，而 KAN 在边缘（“权重”）上有可学习的激活函数。KAN 完全没有线性权重–每个权重参数都由参数化为样条曲线的单变量函数代替。我们的研究表明，这一看似简单的改变使得 KAN 在准确性和可解释性方面都优于 MLP。
Wav-KAN：小波Kolmogorov-Arnold网络
m0_47867638的博客
07-19 2025
摘要 https://arxiv.org/pdf/2405.12832 在本文中，我们介绍了Wav-KAN，这是一种创新的神经网络架构，它利用Wavelet Kolmogorov-Arnold Networks（Wav-KAN）框架来提高可解释性和性能。传统的多层感知机（MLPs）甚至最近的进展如Spl-KAN[1]在可解释性、训练速度、鲁棒性、计算效率和性能方面都面临挑战。Wav-KAN通过将小波函数融入Kolmogorov-Arnold网络结构，解决了这些局限性，使网络能够高效地捕获输入数据的高频和低频
KAN: Kolmogorov-Arnold Networks (arXiv 2024)
Jurio的博客
07-10 3106
【KAN原论文阅读笔记】受Kolmogorov-Arnold表示定理的启发，作者提出Kolmogorov-Arnold Networks（KAN）作为多层感知器（MLPs）的有前途的替代方案。MLP 在节点（“神经元”）上具有固定的激活函数，但 KAN 在边缘（“权重”）上具有可学习的激活函数。KAN 没有线性权重：每个权重参数都被参数化为一个样条线的单变量函数。作者发现，这个看似简单的变化使得 KAN 在准确性和可解释性方面优于 MLP。
[论文翻译]：KAN：科尔莫戈洛夫-阿诺德网络
强化学习曾小健
05-04 3641
受科尔莫戈洛夫-阿诺德表示定理的启发，我们提出了科尔莫戈洛夫-阿诺德网络（KANs）作为多层感知器（MLPs）的有希望的替代方案。虽然MLPs在节点（“神经元”）上有固定的激活函数，但KANs在边缘（“权重”）上有可学习的激活函数。KANs根本没有线性权重 - 每个权重参数都被替换为参数化为样条的单变量函数。我们展示了这个看似简单的改变使得KANs在准确性和可解释性方面优于MLPs。在准确性方面，较小的KANs在数据拟合和PDE求解方面可以达到与较大的MLPs相媲美甚至更好的准确性。
WHAT KAN I SAY？Kolmogorov-Arnold Network (KAN)网络结构介绍及实战（文末送书）
热门推荐
Hello大家好，我是Dream，如果帮得到你，那我深感荣幸！想进粉丝福利群及免费送书群，直接私信我拉你。交流学习、商务合作：https://bbs.youkuaiyun.com/topics/614347534
12-26 3万+
2024年4月，来自MIT、加州理工学院、东北大学等团队的研究，引爆了一整个科技圈：Yes We KAN！ 这种创新方法挑战了多层感知器(Multilayer Perceptron，MLP)的传统观点，为神经网络架构提供了全新的视角，GitHub上收获15k stars。
论文解读：KAN: Kolmogorov–Arnold Networks
zenRRan的博客
05-07 1万+
五一假期刚开始没两天的时候，刷到了一篇火遍国内外AI圈的论文，叫做 KAN: Kolmogorov–Arnold Networks , 尤其国内某些科技媒体铺天盖地的宣传更是让我提起了兴趣，在假期结束之前，抽个空读一下看看是怎么个事。读了之后发现，仅仅只是高数、线代和概率论这些数学知识是看不懂的，最好还需要了解一点数分方面的知识，反正我是借助了ChatGPT才能勉强看完，这里我就从一个简单的科普...
KAN网络
保持学习
05-11 1393
KAN论文精读
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

坐望云起

如果觉得有用，请不吝打赏

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值