数据结构和算法 递归/循环遍历二叉树

原创 于 2022-04-30 06:00:00 发布 · 751 阅读 · 1 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#数据结构 #散列表 #二叉树 #循环遍历二叉树 #递归遍历二叉树

本文介绍了二叉树的基本概念及其五种形态，并通过C++代码展示了递归和循环遍历二叉树的方法。递归遍历简洁但效率受节点数量影响，循环遍历利用栈结构避免了这个问题。代码示例中，二叉树的节点包含数据，并实现了添加、遍历和销毁功能。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

1、二叉树概述

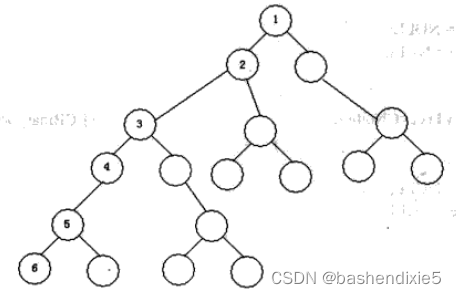
        二叉树是一种常见的数据结构，其特点是每一个节点元素都最多包含两个子节点，左子节点和右子节点。

        二叉树可以有5种基本形态，空二叉树、只有根节点、右子树为空，左子树为空，左、右子树均非空。

        二叉树有着广泛的应用，如描述语法结构，表示数据库对象的层次关系。

2、递归遍历二叉树

        下面c++代码定义了二叉树类模板和节点类型，然后使用递归方法进行二叉树遍历。递归遍历的缺点是如果二叉树的节点较多，系统性能会收到很大影响。

#include "stdafx.h"
#include <iostream.h>
#include <memory.h>

template <class  Type>						//定义二叉树类模板
class CBinaryTree
{
private:
	int		m_nNodeCount;				//节点数量
	Type*	m_pRootNode;					//根节点
public:
	CBinaryTree()							//构造函数
	{
		m_pRootNode = new Type();			//构建根节点
		m_nNodeCount = 1;					//设置节点数量
		InitBinaryTree();					//初始化二叉树
	}	
	Type* GetRootNode() const				//获取根节点
	{
		return m_pRootNode;
	}
	void InitBinaryTree()						//初始化二叉树
	{
		Type* pTmpNode = m_pRootNode;
		for(int i=1; i< 11; i++)					//添加10个节点
		{
			Type* pNode = new Type;
			pNode->m_nData = i;
label:		bool bRet = AddNode(pTmpNode, pNode, 0);	//添加左节点
			if (!bRet)								//添加失败，则添加右节点
			{
				bRet = AddNode(pTmpNode, pNode, 1);
			}
			if (!bRet)										//该节点左右节点都存在
			{
				pTmpNode = pTmpNode->m_pLeftNode;
				goto label;
			}
		}
	} 
	
	void IterateBinaryTree(Type *pNode)						//递归遍历二叉树
	{
		if (pNode != NULL)									//如果节点不为空
		{
			cout << "节点数据: " << pNode->m_nData << endl;		//输出节点数据
		}
		if (pNode->m_pLeftNode != NULL)						//如果左节点不为空
		{
			IterateBinaryTree(pNode->m_pLeftNode);				//递归调用
		}
		if (pNode->m_pRightNode != NULL)						//如果右节点不为空
		{
			IterateBinaryTree(pNode->m_pRightNode);			//递归调用
		}
	}
	bool AddNode(Type *pDestation, Type *pNode, int nFlag = 0)		//在为节点添加数据
	{
		if (pDestation != NULL && pNode != NULL)
		{
			if (nFlag)										//添加右节点
			{
				if (!pDestation->m_pRightNode)
				{
					pDestation->m_pRightNode = pNode;
				}
				else										//pDestation已经有了右节点
				{
					return false;
				}
			}
			else											//添加左节点
			{
				if (!pDestation->m_pLeftNode)
				{
					pDestation->m_pLeftNode = pNode;
				}
				else										//pDestation已经有了右节点
				{
					return false;
				}
			}
			m_nNodeCount++;
			return true;
		}
		return false;
	}
	
	void DestroyBinaryTree(Type *pNode)						//释放二叉树节点
	{
		Type *pLeftNode, *pRightNode;
		if (pNode != NULL)									//如果节点不为空
		{
			pLeftNode = pNode->m_pLeftNode;					//记录左子节点
			pRightNode = pNode->m_pRightNode;				//记录右子节点
			delete pNode;									//释放当前节点
			pNode = NULL;
		}
		if (pLeftNode != NULL)								//如果左子节点不为空
		{
			DestroyBinaryTree(pLeftNode);
		}	
		if (pRightNode != NULL)								//如果右子节点不为空
		{
			DestroyBinaryTree(pRightNode);
		}
	}
	virtual ~CBinaryTree()									//析构函数
	{
		DestroyBinaryTree(m_pRootNode);						//释放二叉树节点
	}
};

class CNode												//定义节点类型
{
private:
	CNode	*m_pLeftNode;									//左子节点
	CNode	*m_pRightNode;								//右子节点
	int		m_nData;										//节点数据
public:
	CNode()												//默认构造函数	
	{
		m_pLeftNode		= NULL;
		m_pRightNode	= NULL;
		m_nData			= 0;
	}
	friend class CBinaryTree<CNode>;						//将CBinary声明为友元类
	virtual ~CNode()
	{
		m_pLeftNode		= NULL;
		m_pRightNode	= NULL;
		m_nData			= 0;		
	}
};



int main(int argc, char* argv[])
{
	CBinaryTree<CNode> BinaryTree;							//定义二叉树对象
	BinaryTree.IterateBinaryTree(BinaryTree.GetRootNode());		//递归遍历二叉树
	return 0;
}

3、循环遍历二叉树

        利用循环遍历二叉树，需要设计栈的结构，用于存储遍历的节点，利用栈结构的后进先出的特点，遍历所有节点。主要思路是首先根据根节点遍历其下左节点，直至左子节点为空。

 

#include "stdafx.h"
#include <iostream.h>
#include <memory.h>


//设计一个栈结构
template <class Type>
class  CStact
{
private:
	Type *m_pBottom;	//栈底
	Type *m_pTop;		//栈顶
	int				m_nStackSize;			//栈大小，单位是1个元素
public:
	CStact()
	{
		m_pBottom = NULL;
		m_pTop = NULL;
		m_nStackSize = 30;
	}
	~CStact()								//析构函数						
	{
		  if (m_pBottom != NULL)
		  {
				m_pBottom ++;
				delete [] m_pBottom;
		  }
	}
	bool InitStack(int nStackSize)			//初始化栈
	{
		m_nStackSize = nStackSize;
		try
		{
			m_pBottom = new Type[m_nStackSize];
			m_pBottom--;					//落入栈底
			m_pTop = m_pBottom;				//空栈
		}
		catch(...)
		{
			return false;					//初始化失败
		}
		return true;
	}
	bool Push(Type *pNode)		//入栈
	{
		if (m_pTop - m_pBottom >= m_nStackSize || pNode == NULL)
		{
			return false;					//栈溢出
		}
		m_pTop++;							//移动栈顶指针
		memcpy(m_pTop, pNode, sizeof(Type));
		return true;
	}
	bool Pop(Type *pNode)			//出栈
	{
		if (m_pTop == m_pBottom)				//空栈
		{
			return false;
		}
		memcpy(pNode, m_pTop, sizeof(Type));
		m_pTop--;
		return true;
	}
	bool GetTop(Type *pNode)		//获取栈顶数据
	{
		if (m_Top == m_pBottom)				//空栈
		{
			return false;
		}
		memcpy(pNode, m_pTop, sizeof(Type));
		return true;
	}
	bool IsEmpty()							//是否为空栈
	{
		return (m_pTop == m_pBottom);
	}
};


//定义二叉树
template <class  Type>
class CBinaryTree
{
private:
	int		m_nNodeCount;			//节点数量
	Type*	m_pRootNode;			//根节点
public:
	CBinaryTree()					//构造函数
	{
		m_pRootNode = new Type();
		m_nNodeCount = 1;
		InitBinaryTree();
	}

	void InitBinaryTree()				//初始化二叉树
	{
		Type* pTmpNode = m_pRootNode;
		for(int i=1; i< 11; i++)		//添加10个节点
		{
			Type* pNode = new Type;
			pNode->m_nData = i;
label:		bool bRet = AddNode(pTmpNode, pNode, 0);	//添加左节点
			if (!bRet)									//添加失败，则添加右节点
			{
				bRet = AddNode(pTmpNode, pNode, 1);
			}
			if (!bRet)									//该节点左右节点都存在
			{
				pTmpNode = pTmpNode->m_pLeftNode;
				goto label;
			}
		}
	} 

	void LoopBinaryTree()					//循环遍历二叉树
	{
		CStact<CNode> Stack;							//定义一个栈
		Stack.InitStack(m_nNodeCount);					//初始化栈
		Stack.Push(m_pRootNode);						//将根节点入栈
		Type *pNode = m_pRootNode;
		while(!Stack.IsEmpty())
		{
			if (pNode)
			{
				while(pNode)								//遍历左子节点，直到尽头
				{
					Stack.Push(pNode->m_pLeftNode);			//入栈
					pNode = pNode->m_pLeftNode;
				}
			}
			else
			{
				Type Node;
				bool bRet = Stack.Pop(&Node);							//回退指针	
				if (bRet)
				{
					cout << "节点数据: " << Node.m_nData << endl;
				}
				bRet = Stack.Pop(&Node);
				if (bRet)
				{
					cout << "节点数据: " << Node.m_nData << endl;
				}
				if (bRet && Node.m_pRightNode != NULL)
				{
					Stack.Push(Node.m_pRightNode);
					pNode = Node.m_pRightNode;
				}				
			}
		}
	}

	bool AddNode(Type *pDestation, Type *pNode, int nFlag = 0)		//在为节点添加数据
	{
		if (pDestation != NULL && pNode != NULL)
		{
			if (nFlag)				//添加右节点
			{
				if (!pDestation->m_pRightNode)
				{
					pDestation->m_pRightNode = pNode;
				}
				else				//pDestation已经有了右节点
				{
					return false;
				}
			}
			else					//添加左节点
			{
				if (!pDestation->m_pLeftNode)
				{
					pDestation->m_pLeftNode = pNode;
				}
				else				//pDestation已经有了右节点
				{
					return false;
				}				
			}
			m_nNodeCount++;
			return true;
		}
		return false;
	}
	
	void DestroyBinaryTree(Type *pNode)		//释放二叉树节点
	{
		Type *pLeftNode, *pRightNode;
		if (pNode != NULL)
		{
			pLeftNode = pNode->m_pLeftNode;
			pRightNode = pNode->m_pRightNode;
			delete pNode;
			pNode = NULL;
		}
		if (pLeftNode != NULL)
		{
			DestroyBinaryTree(pLeftNode);
		}
		if (pRightNode != NULL)
		{
			DestroyBinaryTree(pRightNode);
		}		
	}

	virtual ~CBinaryTree()			//析构函数
	{
		//释放二叉树节点
		DestroyBinaryTree(m_pRootNode);
	}
};


//定义节点类型
class CNode
{
private:
	CNode	*m_pLeftNode;	//左子节点
	CNode	*m_pRightNode;	//右子节点
	int		m_nData;		//节点数据
public:
	CNode()					//默认构造函数					
	{
		m_pLeftNode		= NULL;
		m_pRightNode	= NULL;
		m_nData			= 0;
	}
	friend class CBinaryTree<CNode>;
	virtual ~CNode()
	{
		m_pLeftNode		= NULL;
		m_pRightNode	= NULL;
		m_nData			= 0;		
	}
};


int main(int argc, char* argv[])
{
	CBinaryTree<CNode> BinaryTree;
	BinaryTree.LoopBinaryTree();
	return 0;
}

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

坐望云起

如果觉得有用，请不吝打赏

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值