一、交换排序
1、冒泡排序
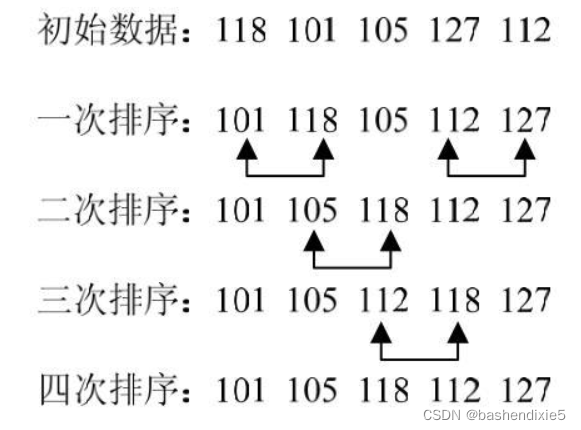
冒泡排序(Bubble Sort)算法是所有排序算法中最简单、最基本的一种。冒泡排序算法的思路就是交换排序,通过相邻数据的交换来达到排序的目的。
平均速度为O(n2),最坏情况下的速度为O(n2);
冒泡排序算法通过多次比较和交换来实现排序,其排序流程如下:
(1)对数组中的各数据,依次比较相邻的两个元素的大小。
(2)如果前面的数据大于后面的数据,就交换这两个数据。经过第一轮的多次比较排序后,便可将最小的数据排好。
(3)再用同样的方法把剩下的数据逐个进行比较,最后便可按照从小到大的顺序排好数组各数据。
public static <T extends Comparable<T>> T[] bubble_sort(T[] array) {
for (int i = 1, size = array.length; i < size; ++i) {
boolean swapped = false;
for (int j = 0; j < size - i; ++j) {
//判断大小
if (greater(array[j], array[j + 1])) {
//交换位置
swap(array, j, j + 1);
swapped = true;
}
}
if (!swapped) {
break;
}
}
return array;
}
2、快速排序
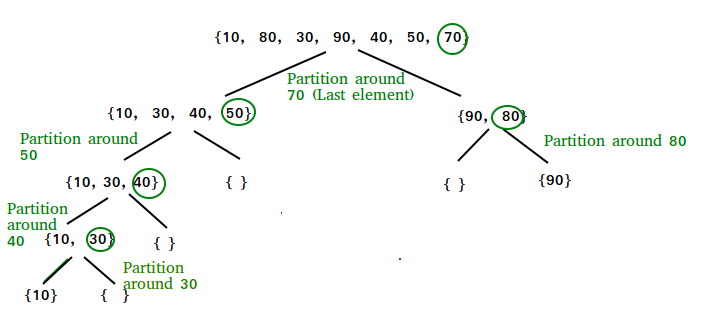
快速排序(Quick Sort)算法和冒泡排序算法类似,都是基于交换排序思想的。快速排序算法对冒泡排序算法进行了改进,从而具有更高的执行效率。快速排序是一种分治算法。它选择一个元素作为轴,并围绕选择的轴对给定数组进行分区。有许多不同版本的 quickSort 以不同的方式选择轴。
平均速度为O(nlogn),最坏情况下的速度为O(n2)
快速排序算法通过多次比较和交换来实现排序,其排序流程如下:
(1)首先设定一个分界值,通过该分界值将数组分成左右两部分。
(2)将大于等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边。此时,左边部分中各元素都小于等于分界值,而右边部分中各元素都大于等于分界值。
(3)然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样将左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
(4)重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左、右两部分各数据排序完成后,整个数组的排序也就完成了。
package com.algorithm.demo.algorithms;
import static com.algorithm.demo.algorithms.SortUtils.*;
public class QuickSortAlgorithm {
/**
* 对外的方法
*
* @param array 要排序的数组,按升序对数组进行排序
*/
public static <T extends Comparable<T>> T[] sort(T[] array) {
doSort(array, 0, array.length - 1);
return array;
}
/**
* 排序方法
*
* @param left The first index of an array
* @param right The last index of an array
* @param array The array to be sorted
*/
private static <T extends Comparable<T>> void doSort(T[] array, int left, int right) {
if (left < right) {
int pivot = randomPartition(array, left, right);
doSort(array, left, pivot - 1);
doSort(array, pivot, right);
}
}
/**
* 随机化数组以避免基本有序的序列
* Ramdomize the array to avoid the basically ordered sequences
*
* @param array The array to be sorted
* @param left The first index of an array
* @param right The last index of an array
* @return the partition index of the array
*/
private static <T extends Comparable<T>> int randomPartition(T[] array, int left, int right) {
int randomIndex = left + (int) (Math.random() * (right - left + 1));
swap(array, randomIndex, right);
return partition(array, left, right);
}
/**
* 此方法查找数组的分区索引
* This method finds the partition index for an array
*
* @param array The array to be sorted
* @param left The first index of an array
* @param right The last index of an array Finds the partition index of an
* array
*/
private static <T extends Comparable<T>> int partition(T[] array, int left, int right) {
int mid = (left + right) >>> 1;
T pivot = array[mid];
while (left <= right) {
while (less(array[left], pivot)) {
++left;
}
while (less(pivot, array[right])) {
--right;
}
if (left <= right) {
swap(array, left, right);
++left;
--right;
}
}
return left;
}
}
二、选择排序
选择排序(Selection Sort)算法也是比较简单的排序算法,其思路比较直观。选择排序算法在每一步中选取最小值来重新排列,从而达到排序的目的。
平均速度O(n2),最坏情况下的速度为O(n2)
选择排序算法通过选择和交换来实现排序,其排序流程如下:
(1)首先从原始数组中选择最小的1个数据,将其和位于第1个位置的数据交换。
(2)接着从剩下的n-1个数据中选择次小的1个数据,将其和第2个位置的数据交换。
(3)然后不断重复上述过程,直到最后两个数据完成交换。至此,便完成了对原始数组的从小到大的排序。

插入排序算法在对n个数据进行排序时,无论原数据有无顺序,都需要进行n-1步的中间排序。这种排序方法思路简单直观,在数据已有一定顺序的情况下,排序效率较好。但如果数据无规则,则需要移动大量的数据,其排序效率也不高。
public static <T extends Comparable<T>> T[] selection_sort(T[] arr) {
int n = arr.length;
for (int i = 0; i < n - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < n; j++) {
if (arr[minIndex].compareTo(arr[j]) > 0) {
minIndex = j;
}
}
if (minIndex != i) {
T temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
return arr;
}
三、插入排序
插入排序(Insertion Sort)算法通过对未排序的数据执行逐个插入至合适的位置而完成排序工作。插入排序算法的思路比较简单,应用比较多。
平均速度为O(n2),最坏情况下的速度为O(n2)
插入排序算法通过比较和插入来实现排序,其排序流程如下:
(1)首先对数组的前两个数据进行从小到大的排序。
(2)接着将第3个数据与排好序的两个数据比较,将第3个数据插入合适的位置。
(3)然后,将第4个数据插入已排好序的前3个数据中。
(4)不断重复上述过程,直到把最后一个数据插入合适的位置。最后,便完成了对原始数组从小到大的排序。

/**
* 插入排序
* @param array
* @return
*/
public static <T extends Comparable<T>> T[] insertion_sort(T[] array) {
for (int i = 1; i < array.length; i++) {
T insertValue = array[i];
int j;
for (j = i - 1; j >= 0 && less(insertValue, array[j]); j--) {
array[j + 1] = array[j];
}
if (j != i - 1) {
array[j + 1] = insertValue;
}
}
return array;
}
四、合并排序
合并排序(Merge Sort)算法就是将多个有序数据表合并成一个有序数据表。如果参与合并的只有两个有序表,则称为二路合并。对于一个原始的待排序序列,往往可以通过分割的方法来归结为多路合并排序。下面以二路合并为例,来介绍合并排序算法。
平均速度为O(nlogn),最坏情况下的速度为O(nlogn)。
一个待排序的原始数据序列进行合并排序的基本思路是,首先将含有n个结点的待排序数据序列看作由n个长度为1的有序子表组成,将其依次两两合并,得到长度为2的若干有序子表;然后,再对这些子表进行两两合并,得到长度为4的若干有序子表……,重复上述过程,一直到最后的子表长度为n,从而完成排序过程。





class MergeSort
{
void merge(int arr[], int l, int m, int r)
{
// Find sizes of two subarrays to be merged
int n1 = m - l + 1;
int n2 = r - m;
/* Create temp arrays */
int L[] = new int[n1];
int R[] = new int[n2];
/*Copy data to temp arrays*/
for (int i = 0; i < n1; ++i)
L[i] = arr[l + i];
for (int j = 0; j < n2; ++j)
R[j] = arr[m + 1 + j];
/* Merge the temp arrays */
// Initial indexes of first and second subarrays
int i = 0, j = 0;
// Initial index of merged subarray array
int k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
}
else {
arr[k] = R[j];
j++;
}
k++;
}
/* Copy remaining elements of L[] if any */
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
/* Copy remaining elements of R[] if any */
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
// Main function that sorts arr[l..r] using
// merge()
void sort(int arr[], int l, int r)
{
if (l < r) {
// Find the middle point
int m =l+ (r-l)/2;
// Sort first and second halves
sort(arr, l, m);
sort(arr, m + 1, r);
// Merge the sorted halves
merge(arr, l, m, r);
}
}
/* A utility function to print array of size n */
static void printArray(int arr[])
{
int n = arr.length;
for (int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
// Driver code
public static void main(String args[])
{
int arr[] = { 12, 11, 13, 5, 6, 7 };
System.out.println("Given Array");
printArray(arr);
MergeSort ob = new MergeSort();
ob.sort(arr, 0, arr.length - 1);
System.out.println("\nSorted array");
printArray(arr);
}
}
/* This code is contributed by Rajat Mishra */
五、Shell排序
Shell排序算法严格来说基于插入排序的思想,其又称为希尔排序或者缩小增量排序。Shell排序算法的排序流程如下:
(1)将有n个元素的数组分成n/2个数字序列,第1个数据和第n/2+1个数据为一对,…
(2)一次循环使每一个序列对排好顺序。
(3)然后,再变为n/4个序列,再次排序。
(4)不断重复上述过程,随着序列减少最后变为一个,也就完成了整个排序。
平均速度为O(n3/2),最坏情况下的速度为O(n2)。
class ShellSort
{
//打印
static void printArray(int arr[])
{
int n = arr.length;
for (int i=0; i<n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
//排序方法
int sort(int arr[])
{
int n = arr.length;
// 从大差距开始,然后缩小差距
for (int gap = n/2; gap > 0; gap /= 2)
{
for (int i = gap; i < n; i += 1)
{
int temp = arr[i];
int j;
for (j = i; j >= gap && arr[j - gap] > temp; j -= gap)
arr[j] = arr[j - gap];
arr[j] = temp;
}
}
return 0;
}
public static void main(String args[])
{
int arr[] = {12, 34, 54, 2, 3};
System.out.println("Array before sorting");
printArray(arr);
ShellSort ob = new ShellSort();
ob.sort(arr);
System.out.println("Array after sorting");
printArray(arr);
}
}
六、桶排序
桶排序是一种排序算法,它将元素分成多个组,称为桶。桶排序中的元素首先被统一分成称为桶的组,然后通过任何其他排序算法对它们进行排序。之后,以排序的方式收集元素。
执行桶排序的基本过程如下:
首先,将范围划分为固定数量的桶。
然后,将每个元素扔到相应的桶中。
之后,通过应用排序算法对每个存储桶进行单独排序。
最后,连接所有已排序的存储桶。
桶排序的最佳和平均情况复杂度是O(n + k),桶排序的最坏情况复杂度是O(n 2 )
import java.util.*;
import java.util.Collections;
class BucketSort {
// Function to sort arr[] of size n
// using bucket sort
static void bucketSort(float arr[], int n)
{
if (n <= 0)
return;
// 1) Create n empty buckets
@SuppressWarnings("unchecked")
Vector<Float>[] buckets = new Vector[n];
for (int i = 0; i < n; i++) {
buckets[i] = new Vector<Float>();
}
// 2) Put array elements in different buckets
for (int i = 0; i < n; i++) {
float idx = arr[i] * n;
buckets[(int)idx].add(arr[i]);
}
// 3) Sort individual buckets
for (int i = 0; i < n; i++) {
Collections.sort(buckets[i]);
}
// 4) Concatenate all buckets into arr[]
int index = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < buckets[i].size(); j++) {
arr[index++] = buckets[i].get(j);
}
}
}
// Driver code
public static void main(String args[])
{
float arr[] = { (float)0.897, (float)0.565,
(float)0.656, (float)0.1234,
(float)0.665, (float)0.3434 };
int n = arr.length;
bucketSort(arr, n);
System.out.println("Sorted array is ");
for (float el : arr) {
System.out.print(el + " ");
}
}
}
七、堆排序(HeapSort)
与归并排序一样,但不同于插入排序的是,堆排序的时间复杂度是。而与插入排序相同,但不同于归并排序的是堆排序同样具有空间原址性:任何时候都只需要常数个额外的元素空间存储临时数据。
二叉(堆)可以被看成是一个数组,它可以被看成一个近似的完全二叉树。树上的每一个节点对应数组中的一个元素。
public class HeapSort {
public void sort(int arr[])
{
int n = arr.length;
// 构建堆(重新排列数组)
for (int i = n / 2 - 1; i >= 0; i--)
heapify(arr, n, i);
// 一个一个地从堆中提取一个元素
for (int i = n - 1; i > 0; i--) {
// 将当前根移动到末尾
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
//
heapify(arr, i, 0);
}
}
// 堆化以节点 i 为根的子树,节点 i 是 arr[] 中的索引。 n 是堆的大小
void heapify(int arr[], int n, int i)
{
int largest = i; // Initialize largest as root
int l = 2 * i + 1; // left = 2*i + 1
int r = 2 * i + 2; // right = 2*i + 2
// 如果左孩子大于根
if (l < n && arr[l] > arr[largest])
largest = l;
// 如果右孩子大于迄今为止最大的孩子
if (r < n && arr[r] > arr[largest])
largest = r;
// 如果最大不是根
if (largest != i) {
int swap = arr[i];
arr[i] = arr[largest];
arr[largest] = swap;
// 递归地堆积受影响的子树
heapify(arr, n, largest);
}
}
/*打印大小为 n 的数组的实用程序函数 */
static void printArray(int arr[])
{
int n = arr.length;
for (int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
System.out.println();
}
// Driver code
public static void main(String args[])
{
int arr[] = { 12, 11, 13, 5, 6, 7 };
int n = arr.length;
HeapSort ob = new HeapSort();
ob.sort(arr);
System.out.println("Sorted array is");
printArray(arr);
}
}
八、多路归并排序
对于一些大的文件,由于计算机的内存有限,往往不能直接将其读入内存进行排序。这时可以采用多路归并排序法,将文件划分为几个能够读入内存的小部分,然后分别读入进行排序,经过多次处理即可完成大文件的排序。








 本文详细介绍了包括冒泡排序、快速排序、选择排序等在内的八种经典排序算法的工作原理及实现方式,涵盖了各种算法的时间复杂度及其适用场景。
本文详细介绍了包括冒泡排序、快速排序、选择排序等在内的八种经典排序算法的工作原理及实现方式,涵盖了各种算法的时间复杂度及其适用场景。



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










