机器学习笔记 - 模拟退火算法

一、什么是模拟退火？

        模拟退火是一种求解无约束和有界约束优化问题的方法。 该方法模拟加热材料然后缓慢降低温度以减少缺陷的物理过程，从而最大限度地减少系统能量。

        模拟退火算法是一种通用概率演算法，用来在一个大的搜索空间内寻找命题的最优解，它是基于Monte-Carlo迭代求解策略的一种随机寻优算法。

        在模拟退火算法的每次迭代中，都会随机生成一个新点。 新点与当前点的距离，或搜索范围，基于一个概率分布，其尺度与温度成正比。 该算法接受所有降低目标的新点，但也以一定的概率接受提高目标的点。 通过接受提高目标的点，该算法避免陷入局部最小值，并且能够全局探索更多可能的解决方案。 随着算法的进行，选择一个退火方案来系统地降低温度。 随着温度的降低，该算法会减小其搜索范围以收敛到最小值。

二、模拟退火算法描述

        模拟退火算法执行以下步骤：

        该算法生成一个随机试验点。 该算法通过具有取决于当前温度的尺度的概率分布来选择试验点与当前点的距离。 您可以使用 AnnealingFcn 选项将试验点距离分布设置为函数。 选择：

        @annealingfast（默认）——步长等于当前温度，方向是均匀随机的。

        @annealingboltz — 步长等于温度的平方根，方向是均匀随机的。

        @myfun — 自定义退火算法，myfun。 有关自定义退火函数语法。

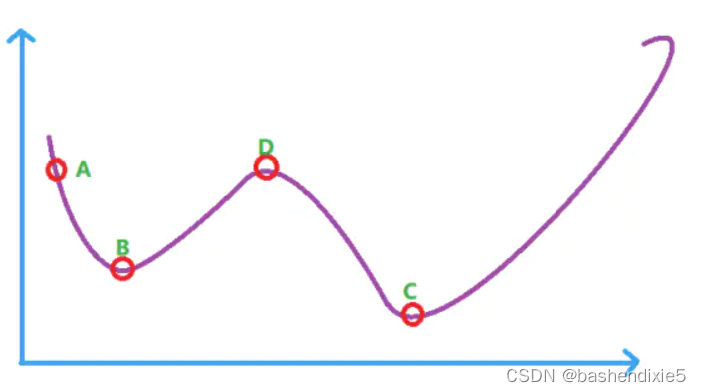
        从下图来说，模拟退火算法在搜索到局部最优解B后，会以一定的概率接受向右的移动。也许经过几次这样的不是局部最优的移动后会到达BC之间的峰点D，这样一来便跳出了局部最优解B，继续往右移动就有可能获得全局最优解C。如下图：

         算法步骤

        可以看出，算法实际上是两层循环嵌套，外层循环控制温度，内层循环来进行扰动产生新解。随着温度逐渐降低，算法最终由可能收敛到全局最优，这里说有可能的原因是因为，在温度很低时，虽然从地内能状态跳到高内能状态的可能性不大，但是也有可能发生。

 三、应用场景

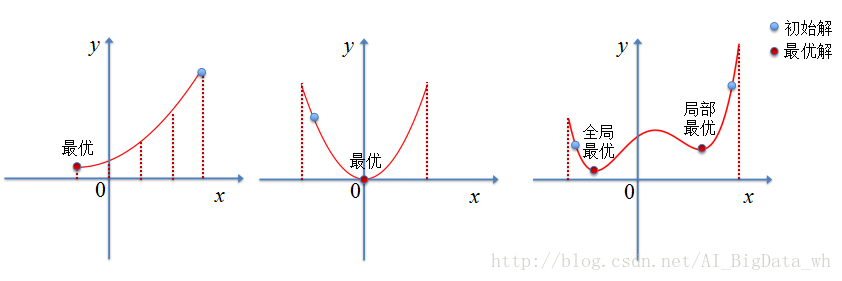
• 如果是离散取值，则可以用穷举法获得问题最优解
• 如果取值连续，且函数是凸函数，则可以用梯度下降等方法获得最优解
• 如果连续非凸，虽说根据已有的近似求解法能够找到问题解，可解是否是最优的还有待考量，很多时候若初始值选择的不好，非常容易陷入局部最优值

 四、使用模拟退火算法解决旅行商问题

        TSP是经典的NP完全问题。精确的解决TSP的算法的时间复杂度是O(2^N), 其中N是节点的个数 。而使用模拟退火算法则可以快速地获得一条近似最优路径。大体的思路如下：

  1) 产生一条新的遍历路径P(i+1)，计算路径P(i+1)的长度L( P(i+1) )。

  2) 若L(P(i+1)) < L(P(i))，则接受P(i+1)为新的路径，否则以模拟退火的那个概率接受P(i+1) ，然后降温。

  3) 重复步骤1，2直到满足退出条件。

/*
 * 使用模拟退火算法(SA)求解TSP问题(以中国TSP问题为例)
 * 参考自《Matlab 智能算法30个案例分析》
 */
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<time.h>
#include<math.h>
#define T0 50000.0  // 初始温度
#define T_end (1e-8)
#define q  0.98   // 退火系数
#define L 1000  // 每个温度时的迭代次数，即链长
#define N 31  // 城市数量
int city_list[N]; // 用于存放一个解

// 中国31个城市坐标
double city_pos[N][2] =
    {
    {1304,2312},{3639,1315},{4177,2244},{3712,1399},
    {3488,1535},{3326,1556},{3238,1229},{4196,1004},
    {4312,790},{4386,570},{3007,1970},{2562,1756},
    {2788,1491},{2381,1676},{1332,695},
    {3715,1678},{3918,2179},{4061,2370},
    {3780,2212},{3676,2578},{4029,2838},
    {4263,2931},{3429,1908},{3507,2367},
    {3394,2643},{3439,3201},{2935,3240},
    {3140,3550},{2545,2357},{2778,2826},
    {2370,2975}};

//函数声明
double distance(double *,double *); // 计算两个城市距离
double path_len(int *);  // 计算路径长度
void  init();  //初始化函数
void create_new(); // 产生新解
// 距离函数
double distance(double * city1,double * city2)
{
    double x1 = *city1;
    double y1 = *(city1+1);
    double x2 = *(city2);
    double y2 = *(city2+1);
    double dis = sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
    return dis;
}

// 计算路径长度
double path_len(int * arr)
{
    double path = 0; // 初始化路径长度
    int index = *arr; // 定位到第一个数字(城市序号)
    for(int i=0;i<N-1;i++)
    {
        int index1 = *(arr+i);
        int index2 = *(arr+i+1);
        double dis = distance(city_pos[index1-1],
                                city_pos[index2-1]);

        path += dis;
    }
    int last_index = *(arr+N-1); // 最后一个城市序号
    int first_index = *arr; // 第一个城市序号
    double last_dis = distance(city_pos[last_index-1],
                                city_pos[first_index-1]);
    path = path + last_dis;
    return path; // 返回总的路径长度
}

// 初始化函数
void init()
{
    for(int i=0;i<N;i++)
        city_list[i] = i+1;  // 初始化一个解
}

// 产生一个新解
// 此处采用随机交叉两个位置的方式产生新的解
void create_new()
{
    double r1 = ((double)rand())/(RAND_MAX+1.0);
    double r2 = ((double)rand())/(RAND_MAX+1.0);
    int pos1 = (int)(N*r1); //第一个交叉点的位置
    int pos2 = (int)(N*r2);
    int temp = city_list[pos1];
    city_list[pos1] = city_list[pos2];
    city_list[pos2] = temp;   // 交换两个点
}

// 主函数
int main(void)
{
    srand((unsigned)time(NULL)); //初始化随机数种子
    time_t start,finish;
    start = clock(); // 程序运行开始计时
    double T;
    int count = 0; // 记录降温次数
    T = T0; //初始温度
    init(); //初始化一个解
    int city_list_copy[N]; // 用于保存原始解
    double f1,f2,df; //f1为初始解目标函数值，
                     //f2为新解目标函数值，df为二者差值

    double r; // 0-1之间的随机数，用来决定是否接受新解
    while(T > T_end) // 当温度低于结束温度时，退火结束
    {
        for(int i=0;i<L;i++)
        {
            // 复制数组
            memcpy(city_list_copy,city_list,N*sizeof(int));
            create_new(); // 产生新解
            f1 = path_len(city_list_copy);
            f2 = path_len(city_list);
            df = f2 - f1;
            // 以下是Metropolis准则
            if(df >= 0)
            {
                r = ((double)rand())/(RAND_MAX);
                if(exp(-df/T) <= r) // 保留原来的解
                {
                    memcpy(city_list,city_list_copy,N*sizeof(int));
                }
            }
        }
        T *= q; // 降温
        count++;
    }
    finish = clock(); // 退火过程结束
    double duration = ((double)(finish-start))/CLOCKS_PER_SEC; // 计算时间
    printf("模拟退火算法，初始温度T0=%.2f,降温系数q=%.2f,每个温度迭代%d次,共降温%d次，得到的TSP最优路径为:\n",T0,q,L,count);
    for(int i=0;i<N-1;i++)  // 输出最优路径
    {
        printf("%d--->",city_list[i]);
    }
    printf("%d\n",city_list[N-1]);
    double len = path_len(city_list); // 最优路径长度
    printf("最优路径长度为:%lf\n",len);
    printf("程序运行耗时:%lf秒.\n",duration);
    return 0;
}

五、opencv中的模拟退火 

        opencv中未实现模拟退火算法，但是声明了一个接口。

        下面是原文说明，大意是说 “此类声明了模拟退火优化算法中使用的系统状态的示例接口。此类未在 C++ 代码中定义，不能直接使用 - 您需要使用相同方法自己实现。”

This class declares example interface for system state used in simulated annealing optimization algorithm.

This class is not defined in C++ code and can't be use directly - you need your own implementation with the same methods.