codeforces1516D. Cut（质因数分解+倍增算法）

codeforces1516D. Cut（质因数分解+倍增算法）

因为C没写出来，所以就跑过来写D(lll￢ω￢)

题意：给定一个长度为n的整数序列a，有m个询问。每次询问一个区间【l，r】，问能最少能将该区间分成几个完美的子区间，


定义：
       1、子区间需要连续
       2、完美子区间表示该区间内所有数的乘积为其所有数的最小公倍数

思路：
       完美序列的要求其实就是该区间内的所有数要互质。
怎么分割才是最合理的呢？
必然是从前往后，把能互质的都放在一个区间，一旦不能互质，就另开一个区间去存就好了，这样子必然是满足最小。
但是问题在于m的数目很大，每次都去遍历必然会超时，而且还要判断互质，那必然是不可能完成的。
所以，我们就要先对数据进行处理，得到对数据得到一个记忆化。
怎么处理？得到什么？
我这里定义一个mx数组，定义为，从i位置起，往后所能保证得到的最长的完美区间的位置，也就是mx[i] = j,表示i位置起，到j位置位置，其中的数都互质。
然后通过倍增算法，来跑一遍就可以了。

那么怎么得到mx数组呢？以及判断区间互质呢？
我们不难想到要用双指针判断长度以及质因数分解。

简单说一下原理：
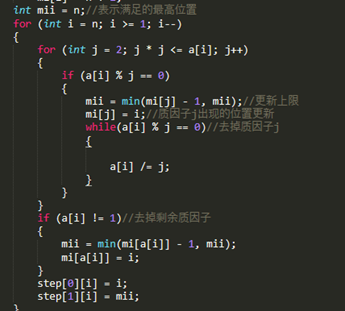
互质，那么必然所有数的质因子不能存在有一样。分解质因子的就可以更新出这个质因子的位置i。然后，如果有前面的数出现了这个质因子，那么就不能超过这个质因子的位置i，因为超过就会出现重复质因子，所以要取出这个数所有的质因子的最小位置，然后mii作为双指针的右边界，来保证右边的数也满足条件的综合最小值，可以保证不互质。
然后就是跑一下倍增就好了。

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<set>
#include<stack>
#include<vector>
#include<queue>
#include<unordered_map>
#include<stdio.h>
using namespace std;
const int MAXN = 3e5 + 7;
typedef long long ll;
#define INFll 9223372036854775807
#define INF 0x3f3f3f3f
#define dbg(x) cout << #x << " = " << x << endl;
#define lowbit(n) (n&-n)
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
const ll mod = 1e9 + 7;
ll a