算法导论学习《视频》

很明显，啃算法导论是我必须要做的事情，参考《算法导论》b站

算法导论分为两个部分，第一部分为算法分析，第二部分为算法设计。

算法分析关注性能，也就是时间复杂度。

第一节课   算法分析

T（n）表示是期望运行时间，是关于输入规模n的函数。

我们需要一个有关输入的统计分布假设，不然期望运行时间无从谈起。常见情况就是均匀分布，就是输入是每种输入n都是等可能出现的。

那么最好情况输入（欺骗）

1.1 渐进分析技术（伟大的算法分析技术）

忽略常量，不去真正比较时间，而是关注T(n）与n的增长趋势。

关注三个符号，就是上界、中界、下界？

例子1

插入排序的最坏情况下，计算其运行次数，使用渐进分析就是

 

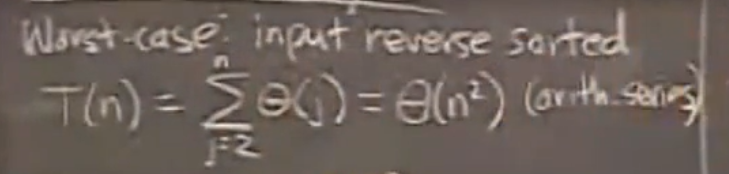
O（n2），使用一点点算术级数的小技巧就可以，这里的O是一种描述符号。

例子2

然后又是合并排序

两个列表合并排序的时间复杂度仅仅是O（n）的，是线性的。那么对于合并排序，可以有一个递归表达式

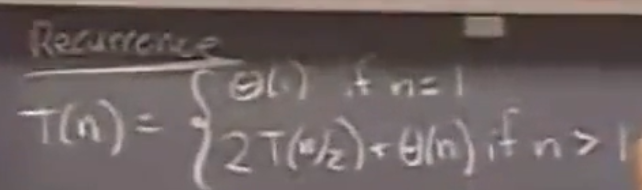
就会得到分析的递推树，问题是树有logn那么高、树的叶子节点就是n个。自然就可以得到O（nlogn）复杂度。

那么就可以得到归并排序比插入排序快的结论。

 

 

第二节课   渐进符号、递归和解法（数学角度）

1 定义

1.1    基于O（）符号的数学严格定义，待写

会有O（）的不对称，还有其数学形式化定义，还有其误差分析，O表示上界。

 

1.2 

  现在是下界的数学严格定义了，（可能也是最好情况的时间复杂度分析），待写

 

 

2 应用

2.1 解递归式

   有三种方法，代换法和猜想法，递归树法（一层层相加，再全部加起来）。其中代换法比价精确，而递归树法不太推荐，只是比较直观而已。

 

 

例子：

 

第三节课 分治法

这里主要就归并排序，和利用1,2节课的知识对算法进行分析。

 

 

第4节课  快排及其随机化算法

4.1 快排本身算法

4.2  快排正确性分析

4.3  快排算法分析

    4.3.1  最优、最坏、最好最坏交换输入时的时间复杂度分析

         这个分析还挺常规

         最优情况就是每次都是刚好每次划分主元都是从中间划分，这样的时间复杂度

T（n）=2T（n/2） +O(n),为O（nlogn）利用之前学习的主成分分析法。

         最差情况就是每次分割都是最左边或者最右边，对应于数据是输入有序的。时间复杂度为O（n2）。

        最好最坏交换输入时，用代换法进行分析

 

 

     4.3.2  随机选择主元的时间复杂度分析

为什么选择它，因为它易于分析

它有几个特点：

• 输入的顺序无关紧要
• 无需对输入序列分布做任何假设，因为是随机选择主元

我们用指示器随机变量来分析其时间复杂度

指示器随机变量可以很好地帮助你去求一大推东西的和。

利用指示器变量的期望，我们发现指示器变量将期望和概率等同起来，我们再写出入随机快排的

 

再利用对T（n）求期望，利用和的期望等于期望的和。

经过对期望的求，可以得到

我们要证明其为O（nlogn），如何证明？

利用指示器随机变量来随机化输入分布，构建求解T（n）的表达式，可以得到随机化的输入对应的时间复杂度分析。

接下来课程就让我们直接证明其小于O（a*n*logn）即可

 

 

第5节课    线性时间排序

 

         这节课很有意思，有点像陶哲轩《科研的简明行程》中的一步，就是将解决当前问题的多种方法归为一个大一统的模型，是该大一统模型在不同条件下导出了多种方法，从而利用该大一统模型得出多种方法的共同性质。

本节课关注两个部分

• 将之前所学的快排、归并、堆排序，将其归为比较模型（大一统模型）中，并且提出决策树模型，并证明所有基于比较的排序算法都可以转为决策树模型，进而利用决策树模型的最小数深度得到一个定理（所有基于比较的排序算法，其时间复杂度不会小于O（nlogn））
• 探索在某些特定条件下，比O（nlong）更快的线性排序算法

5.1 比较模型和决策树模型的定理

所有基于比较模型的排序算法都可以用决策树模型来画出，该决策树画出了排序算法所有的进行步骤，进而可得该决策树的叶子结点数目为n的阶乘个，同时也可得该决策树的最短树深为O（nlogn）（利用树高h和叶子节点总数及斯特林公式可以得到其下界），并且对于任意的随机化输入，其下界仍然保持。证毕。

5.2  比O（nlogn）还要快的方法

有计数排序和基数排序，这两种排序都可以在一定条件下达到O（n）的复杂度。

前者条件为需要排序的数字是一段范围的数，后者不太清楚。

 

6  顺序统计和中值

从一个问题出发，找出一个数组中第k小的元素。

6.1 随机选择法（如何分析其期望时间复杂度）

利用快排算法思想，有一个随机算法

那么如何分析这个随机找第k个最小值的算法期望时间复杂度呢？

按照惯例，分析最好、最坏、平均的算法期望复杂度？

最好的情况：

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

，