一维树状数组几种模板

树状数组模板，单点更新，区间查询：

//树状数组存取、查询log(n),区间求和问题
int n,tree[N]; //tree数组按二进制存,根据n的末尾0的个数存取

int lowbit(int x)
{
    return x&(-x);
}

int Query(int x)  //返回1到x的前缀和
{
    int res=0;
    while(x)
    {
        res+=tree[x];
        x-=lowbit(x);
    }
    return res;
}

void Add(int x,int v)  //实现a[x]+v;
{
    while(x<=n)
    {
        tree[x]+=v;
        x+=lowbit(x);
    }
}

void init()   //输入数据
{
    for(int i=1;i<=n;i++)
    {
        int x;
        scanf("%d",&x);
        Add(i,x);
    }
}

区间更新，单点查询：

//一维树状数组区间修改，单点查询
//原来的值存在a[]里面，多建立个数组c1[](代码中用tree数组表示),注意：c1[i]=a[i]-a[i-1]。
//那么求a[i]的值的时候a[i]=a[i-1]+c1[i]=a[i-2]+c1[i]+c1[i-1]=…..=c1[1]+c1[2]+…+c1[i]。
int a[N],tree[N];
int n;
int lowbit(int x){return x&(-x);}
void updata(int x,int val){  //单点更新
    while(x<=n){
        tree[x]+=val;
        x+=lowbit(x);
    }
}
void regionUpdata(int x,int y,int val){ //区间更新，实现a[x]~a[y]+val
    updata(x,val);
    updata(y+1,-val);
}
int pointQuery(int x){  //单点查询,因为tree数组是差分数组，所以a[x]=tree[1]+tree[2]+...+tree[x]
    int ans=0;
    while(x>0){
        ans+=tree[x];
        x-=lowbit(x);
    }
    return ans;
}
void init(){
    a[0]=0;
    for(int i=1;i<=n;i++){
        updata(i,a[i]-a[i-1]);   //用差分数组初始化树状数组
    }
}

区间跟新，区间查询：

详解：

设原数组第i位的值为ai，di=ai−ai−1，则有(这里认为a0=0)：

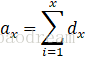
所以有：

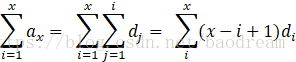
故：

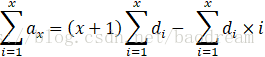
于是我们在更新差分数组的时候再维护一个di*i数组即可。

代码：

ll a[N],tree[N],tree2[N]; //因为tree2是乘积，有可能超int
ll n;
int lowbit(int x){return x&(-x);}
void updata(ll c[],int x,ll val){  //单点更新
    while(x<=n){
        c[x]+=val;
        x+=lowbit(x);
    }
}
ll query(const ll c[],ll x){   //1~x前缀和查询
    ll res = 0;
    while(x>0){
        res+=c[x];
        x-=lowbit(x);
    }
    return res;
}
void regionUpdata(ll x,ll y,ll val){ //区间更新，实现a[x]~a[y]+val
    updata(tree,x,val);
    updata(tree,y+1,-val);
    updata(tree2,x,x*val);
    updata(tree2,y+1,-(y+1)*val);
}
ll regionQuery(ll x,ll y){
    //求1~y的和
    ll ans1 = (y+1)*query(tree,y) - query(tree2,y);
    //求1~x-1的和
    ll ans2 = x*query(tree,x-1) - query(tree2,x-1);
    return ans1-ans2;
}
void init(){
    a[0]=0;
    for(ll i=1;i<=n;i++){
        updata(tree,i,a[i]-a[i-1]);   //用差分数组初始化树状数组
        updata(tree2,i,i*(a[i]-a[i-1]));   
    }
}