华为OD机试D卷C卷 - 围棋的气（C++ Java JavaScript Python C语言）

题目描述

围棋棋盘由纵横各19条线垂直相交组成，棋盘上一共19 x 19 = 361 个交点，对弈双方一方执白棋，一方执黑棋，落子时只能将棋子置于交点上。

“气”是围棋中很重要的一个概念，某个棋子有几口气，是指其上下左右方向四个相邻的交叉点中，有几个交叉点没有棋子，由此可知：

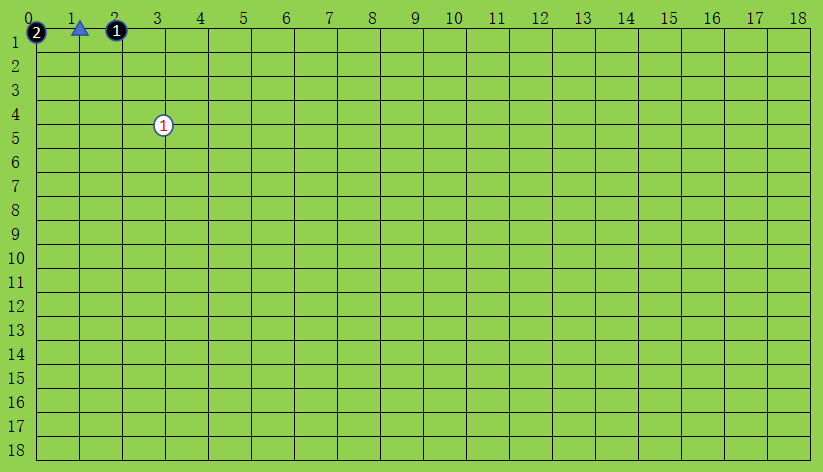
1. 在棋盘的边缘上的棋子最多有 3 口气（黑1），在棋盘角点的棋子最多有2口气（黑2），其他情况最多有4口气（白1）
2. 所有同色棋子的气之和叫做该色棋子的气，需要注意的是，同色棋子重合的气点，对于该颜色棋子来说，只能计算一次气，比如下图中，黑棋一共4口气，而不是5口气，因为黑1和黑2中间红色三角标出来的气是两个黑棋共有的，对于黑棋整体来说只能算一个气。
3. 本题目只计算气，对于眼也按气计算，如果您不清楚“眼”的概念，可忽略，按照前面描述的规则计算即可。

现在，请根据输入的黑棋和白棋得到坐标位置，计算黑棋和白棋一共各有多少气？

输入描述

输入包含两行数据，

每行数据以空格分隔，数据个数是2的整数倍，每两个数是一组，代表棋子在棋盘上的坐标；
坐标的原点在棋盘左上角点，第一个值是行号，范围从0到18；第二个值是列号，范围从0到18。

举例说明：如：

0 5 8 9 9 10
5 0 9 9 9 8

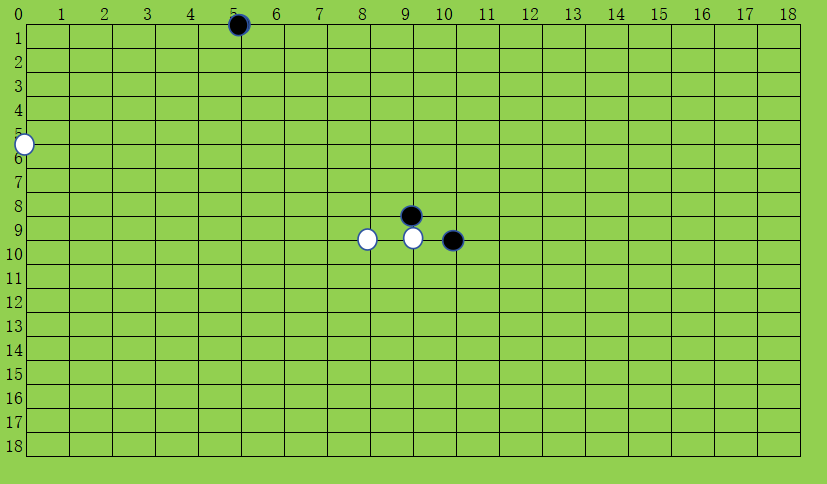
第一行数据表示三个坐标（0, 5）、(8, 9)、(9, 10)
第一行表示黑棋的坐标，第二行表示白棋的坐标。
题目保证输入两行数据，无空行且每行按前文要求是偶数个，每个坐标不会超出棋盘范围。

输出描述

两个数字以空格分隔，第一个数代表黑棋的气数，第二个数代表白棋的气数。

8 7

用例

输入

0 5 8 9 9 10
5 0 9 9 9 8

输出

8 7

说明

数数黑棋一共8口气，数数白棋一共7口气。

解法1

解题思路

在这个例子中，我们有两组棋子的坐标。第一组是黑棋的坐标，第二组是白棋的坐标。

首先，得到两个整数数组，分别代表黑棋和白棋的位置。

黑棋的坐标数组为：{0_5, 8_9, 9_10}
白棋的坐标数组为：{5_0, 9_9, 9_8}

然后，我们计算每组棋子的"气"。

对于黑棋，我们检查每个棋子周围的四个位置，得到的"气"的坐标集合为：{“0_4”, “0_6”, “1_5”, “7_9”, “8_8”, “8_10”, “9_9”, “9_11”, “10_10”}。然后，我们从这个集合中减去黑棋的位置和白棋占据的位置，得到最终的"气"的数量为8。

对于白棋，我们同样检查每个棋子周围的四个位置，得到的"气"的坐标集合为：{“4_0”, “5_1”, “6_0”, “8_9”, “9_8”, “9_10”, “10_9”, “10_8”}。然后，我们从这个集合中减去白棋的位置和黑棋占据的位置，得到最终的"气"的数量为7。

所以，黑棋的"气"的数量为8，白棋的"气"的数量为7。

C++