【Maths】对数 logrithm

Backto Maths Index
在数学中，对数是对求幂的逆运算，正如除法是乘法的逆运算.

如果 $N=a^x(a>0,a̸=1)$, 那么记 $x={\log }_{a}N$, 其中 $a$叫做对数的底数, $N$叫做真数, $x$叫做 以 $a$为底 $N$ 的对数.

特别地,

1. 以 10 为底的对数叫做常用对数(common logarithm), 记做 $lg$
2. 以 $e(=2.71828...)$ 为底的对数称为自然对数(natural logrithm), 记做 $ln$
3. 0 没有对数
4. 在实数范围内, 负数无对数. 在负数范围内, 负数是有对数的

运算法则

1. ${\log }_a(mn)={\log }_{a}m+{\log }_{a}n$
2. ${\log }_a(\frac{m}{n})={\log }_{a}m-{\log }_{a}n$
3. ${\log }_a{m}^n=n{\log }_{a}m$
4. ${\log }_{a}x=\frac{{\log }_{b}x}{{\log }_{b}a}$

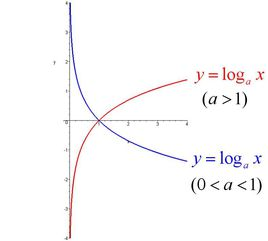
对数函数

复变函数

$e^{ix}=\cos x+i\sin x$, $e$ 是自然对数的底, $i$是虚数单位. 它将指数函数的定义域扩大到负数, 建立了三角函数和指数函数的关系, 被誉为 数学中的天桥.

特别的, 取 $x=\pi$, 得到 $$e^{\pi i}+1=0$$, 这个式子中凝聚了数学最重要的几块儿基石, 被誉为 最美的数学公式

Ref

• 指数与对数: 超级形象完整的总结