练习题随记

最新推荐文章于 2023-03-12 09:26:06 发布

原创最新推荐文章于 2023-03-12 09:26:06 发布 · 721 阅读

0 ·

CC 4.0 BY-SA版权

杂题集专栏收录该内容

1 篇文章

订阅专栏

博主分享了编程竞赛中的经验教训，包括动态规划问题、期望计算、概率模型以及解决策略。提到了在动态区间第k小、工作、抽奖、公正的赌博等问题中的思考和错误，强调了细心和深入理解的重要性。同时，博主还反思了在数学期望、概率计算题目中的误解和计算错误，如抽奖和搜集卡片问题，指出在面对复杂问题时需要更加细致的分析和正确的方程推导。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

动态区间第k小

之前已经写过题解了，链接动态区间第k小，总结：代码要细心一点啊qwq

秀肌肉

莫队裸题，然后没有开longlong又wa又tqwq

小z的袜子

莫队裸题（因为莫队写起来很简单所以就没有用分块），对于 $C (x, y)$ ，令 $t = s i z e (x, y)$ ，则 $C (x, y) = t * (t - 1) / 2$ 即可

弹飞绵羊

同样也是写了题解了owo，但是还是错掉了呢qwq（每一次都会都掉细节emm），太心急了，还有，太不仔细了（感觉写了像白写）。对于思路只有一个模糊的概念，没有一个深刻的认识（好比今天没回答上来的问题）

图书管理员

是字典数裸题，对不起我智障了qwq（没有考虑到可以有多本相同的书，还有借出去如果没有就不借了）

为什么会有一种自己喜欢做水题的错觉

紧急集合

对任意两点求最近公共祖先（思考片刻就会发现不需要求三个的），看哪个花费最少。（这个给个代码？？？？？）

货车运输

最小生成树+lca（其实一开始是以为是图论呢）

从现在开始排列组合！

排队

有6个同学，编号1~6，让六个同学排队，使得5在2前面，求有多少种方案？
正确答案使360，原本自己考虑的是缩点，也就是把5在2前面的情况直接当成一个点计算。然而发现会把中间插数的情况漏掉。
正解有两种，这里介绍其中一种，我们先不考虑5在2前面，单独算的话就是 $C_{6}^{6}$ ,因为5在2前面与2在5前面的数量是相同的(这里很精妙啊)，所以 $C_{6}^{6}/2$ 就可以了。

买糖果（插板插板）

其实不用考虑怎么从5种里面选8个糖果，只需要将8个糖果分成5种类型就行了，是插板法的典型思想呢

体操队形1（缩点啊缩点）

把三个女生看成一个，有点类似于最小生成树的缩点

数学期望

工作

一项工作由甲一个人完成，平均需要4h，而乙有0.4的概率来帮忙，两个人完成平均只需要3h。由于这项工作要么由一个人完成，要么由两个人完成，那么这项工作完成的期望时间？

个人理解的话：是 $e (t) = 4 - 0.4 * 3$ 而实际上应该是 $e (t) = 4 * 0.6 + 0.4 * 3$ （因为一个人做完的情况是60%，算成100%了qwq）

抓球

一个不透明的袋子里装有大小相同的6个白球和5个黑球，从中随意抓一把取出4个球，期望其中所含白球个数x是多少？

个人理解：如果一个个球考虑，则会出现很多种情况，但是如果从整体考虑的话就会发现数据时可算的。
对于取白球有0,1,2,3,4这5种情况。

公正的赌博

设甲，乙两人玩必分胜负的赌博游戏，假定两人的实力相差悬殊，以致两人获胜的概率不等，以至于

抽奖

何老板有一个不透明的袋子，袋中有n张卡片，号码分别为1,2，……，n。从中不放回的随机抽出k张卡片，求所有号码之和的期望值？

个人思考环节：对不起，我忘记该怎么求i张牌出现次数了qwq（智障啊qwq）

题解：

一袋老鼠（哪个公主会恶心到抓老鼠啊！）

原本想的思路是分回合讨论，但是这里给出了可以看成一回合讨论（也就是公主和龙各一回合放到一起讨论）
题解：
状态: $f [i] [j]$ 表示袋中有i白j黑，公主胜的概率，求 $f [w] [b]$
定义: $f [i] [0] = 1, f [0] [i] = 0$
1.抓白： $p 1 = i / （ i + j ）$ 公主胜
2.公主抓黑，龙抓白: $p 2 = j / (i + j) * i / (i + j - 1)$ 公主胜
3.公抓黑，龙抓黑，跑黑： $p 3 = j / (j + i) * (j - 1) / （ i + j - 1 ） * (j - 2) / (i + j - 2)$
4.公抓黑，龙抓黑，跑白: $p 4 = j / (i + j) * (j - 1) / (i + j - 1) * i / (i + j - 2)$

总的方程就是

$f [i] [j] = p 1 * 1 + p 2 * 0 + p 3 * f [i] [j - 3] + p 4 * f [i - 1] [j - 2]$

从今天起你就是我的儿子啦

随记多叉转二叉

for (int i=1;i<=n-1;i++)
{
	cin>>x>>y;
	right[y]=left[x];
	left[x]=y;
}

莎拉公主的困惑

求[1,M!] 与 M！互质的个数？ m<=n
1.[1,m!] :fai(m!)
2.[m!+1,n!]
————未完待续

装糖果（是被隐藏起来的题目呢）

看数据可以得到类似于动归的解法（其实细想就会发现跟动规）完全不沾边系列QAQ
思路大概是：分为1和2两个盒子。
第一个盒子有i种糖果，第二种有m-i种糖果
则可得到：填满第一个盒子的方案数为 $i^n$ ,第二个盒子的方案数为 $m-i)^n$
对于在m个糖果里面选择i个糖果就有 $s g m$ //待定
最后求和 $i$ 属于[1,m-1]
然而这样算是会算重的！

五一完爆比赛题记：
round2
A：（对不起，我是个DP 做签到题的人）
因为只需要点k个蜡烛，会发现k个蜡烛是连续的，所以我们对k个蜡烛的排列方式分类来讨论，1.都在零点左边或者右边，2经过零点，这种情况本身要经过最左边到最右边，然后加上从零点到最左边，和从零点到最右边。
Q：为什么不用考虑中间折返的情况？

B:（个人的思路是用寻找余数的循环节，并且暴力枚举b）
对于b很容易求出范围[k+1,n]（为了保证余数>=k）
然后对于a我们也就能求出范围[1,k)并不满足，而[k,b)则可以满足
同样，倍数的情况也是行得通的所以我们就可以推出一个公式:n/b*(b-k);
但是要考虑无法构成长度为b的区间的情况
例如:n%b若>=k,则有n%b-b+k个满足上述情况

D交换（数形结合）
首先建立数值与下标的联系，然后建立下标与下标之间的联系。然后判断对于的数值能否走到对应的下标，然后进行一个统计。图论的思路最后以并查集进行检验。

E.切序列
首先翻转（就是相当于影响提前计算，然后按照最小表示来进行切割，注意要保证切割数的右边>=3-i）

F中位数们的中位数
算法：二分答案，前缀和，顺序对，树状数组（归并排序）
首先我们得到了B数列的长度n*(n+1)/2，则m所在的位置应该是(n+1)*n/4+1
那么我们就可以使用二分答案
如果小于m的个数> $n * (n + 1) / 4$ ，把m调小
若大于等于m的个数>(n+1)*n/4，把m调大
为了直接获得关于m的位置的相关信息，我们进行如下处理：
设置一个C数组满足若a[i]<m 则c[i]=-1,若a[i]>=m，则c[i]=1；
然后进行一个前缀和操作。目的是检验中位数的左右数的个数:
若sum[y]-sum[x]>=0，那么[x+1,y]位置的中位数>=m
如果将等式进行变换，我们就可以得到:sum[y]>=sum[x]
最后我们得到的只需要顺序对就行了，用树状数组或者归并排序维护。

玩具取名：
啊啊啊啊我真的是个智障···（好吧，也不是第一次了）
对于老板的f[x][y][z]这个状态我居然觉得推不动QAQ，原因是我认为f[x][y][z]中的z应该是一长串的字母，而不是单个字母，但是实际上，一长串字母是一个个组成，最后变成单个字母的。有些时候我想题很容易偏离题意，导致没法推动，并且得到一个比较复杂的过程不知道如何去省略，以及转换思路换一个方式去向，有一点不撞南墙不回头的感觉qwq

已经2019.5.28日了···

赛事直播

一个网络直播平台计划直播今年ioi比赛。网络中的中转点和观看点构成了一个树形结构。这棵树的根是直播点，它将直播比赛。其中观看点是树的叶节点，他们是可能要观看比赛的用户（用户可以选择不看比赛，这样就不用缴观看费）。其他非根节点、非叶节点的中间节点就是直播数据的中间转发点，即中转点。
将比赛数据从树中一个点传到另一个点需要一定的花费。整个直播的费用就是所有传输费用的总和。
每一个用户都给出了自己愿意支付的观看费用。直播公司要决定是否给这个用户提供直播服务。例如：给一个用户（叶节点）直播比赛的花费很大，而这个用户愿意支付的费用却很少时，直播公司可以选择不给他直播。
找到一个方案使得观看ioi直播的客户尽可能多，且直播公司不能亏本（直播的费用不超过所有观看比赛的客户的缴费总和）。

【NOIP2012 day2】疫情控制

对于这道题的思路
首先先算出军队到每个边缘的最短距离，存在dis[maxn][maxn]中（好吧并不是很实际，因为w<10^9次方）
1.判-1
如果军队数少于边境数，则输出-1
2.那么我的第一个思路就是行得通的了，也就是[50000][50000];考虑vector?(这里原本就会炸了，还是照样写)
3.如果当前的边境已经有人把守了，就不讨论
Q？是否可以考虑二分答案，也就是时间尽可能的少？如果超出答案的范围我就选择return
4.对于有多个军队把守的边境，那么肯定走向了dp的道路（）（很明显这里要超时）

思路狭隘的地方：
我的思路中老是会保存已经得到的东西，然后，更细节的地方观察不到。什么叫做更细节的地方呢，我想的话就是，老板能一下子就提取出跟题目相关的有用的信息，并且利用价值很高，而我的呢就会很低，我想的话，以后我在考虑思路的时候，应该首先能把找到的东西列个表，然后对于关键信息打上着重符号，再来校对，看自己的判断能力如何。

何老板的思路补充：
1.移动方向：往上：控制的地点会越多（这一点我没有观察得到，虽然最开始想到了要用最少的人管理更多的地方，但是因为图的原因限制了自己的思路）
2.二分答案（这个考虑到了，应该是练成习惯了，但是这里讲的更详细），假设每支军队可以移动mid分钟
3.军队情况：
1）走不到根节点，就能走多高走多高
2）走到根，再安排（其实这里有漏洞，应该是考虑要控制多少个之后再派多少个军队，但这里不影响，因为可同时进行）
4.分配问题（实际上这里还是考虑到哪些被控制，哪些不被控制）
这里有一个显而易见的贪心，剩余时间多的控制远的，剩余时间少的控制近的

重新梳理题目：
1.因为军队可以同时移动，所以总时间才是最重要的，移动多少支军队到时没有问题，所以不需要考虑积累
2.树中应该发现我应该向上走，以少量的军队控制大批的人
3.贪心原则：剩余时间多的控制远的，剩余时间少的控制近的

注意：
1.Long Long!
2.倍增求往上走的上限（从大到小枚举）
3.注意dfs（由于没有看到dfs问了两次一模一样的问题）

时间复杂度： $n{(log_2n)}^2$

暑期OI，最后三个月QAQ

2019.7.6考试总结

跟初中小学生被虐的好惨啊QAQ，其实题目都是绕了个弯，然后就卡了我半个小时woc，我好菜啊···
可以保留的经验：关于B题的仔细思考（全场唯一的仔细思考）
需要学习的地方：不要老是卡在一道题上面（后面还有个H 题还可以做），很多时候都在错误的道路上一次性闯到底，导致最后一道题都没有时间看

2019.7.7考试总结

woc我不会做动规啊，我看不出B题是动规啊，我推了1个半小时的数学公式，我真的菜到底了QAQ。我可以跟着初中的学动规吗T^T。
这一次A题是一道普及-的题，但是并没有A掉。
可以保留的经验：因为A题我花了一个小时（着实太菜），所以我选择了跳过（可能有点不及时）。
需要学习的地方：B题动规我着实没看出来，C题我似乎有了点思路，但是思考的时间太多了。
所以需要改进的就是思考的时间，以及动规。

关于这两场比赛，都有一个比较严重的失误，基础算法不扎实，不能先判断算法再解题，而是跟着自己的思路自顾自

我是不是有一天没写博客了——2019.7.9考试总结

对不起，第二道题的dp我没有推出来，我好菜QAQ
这里记录一下zz的地方和高端的地方
关于B题，信心满满认为能推出来，没看数据范围，推了个假的n^2算法（两个小时就这样过去了）。第一题很快就看出结果了，但是还是花了半个小时，代码不能保证一次性编译通过，太菜了QAQ
C 和D以至于没有时间看，其实D题很简单，如果做过parity就思路，parity和D题特别的类似，可以考虑从并查集方向思考最后得到要合并到一起从而想到最小生成树。这个故事告诉我们，多积累模型，多做题。我就是做题太少了。
C题有一个高端的写法，因为给出的方程是一个求和公式，一个是前缀和优化，还有一个就是直接将其加到树状数组里面去当做数值。

记录改换赛制之后的第一次得40

我太菜啦QAQ，第一题和第三题都应该全对的（其实第三题模数很大用不着lucas（我居然还抄ppt，我····）），第四题是原题，可惜我之前没有改（要好好改错啊orz orz），第二题的显然emm特别显然，我一点都没有看出来这是显然。（学习rethinking大佬的反向操作，删繁就简）关于第四题，个人觉得自己之前的那道题还是没有理解到，因为我还是在想怎么去做删除操作。

咳咳咳好好写博客：
A题：不是很难，但是注意用BKDRhash容易出现重复的，方法是换一种hash或者直接用map以及不用hash（我打成了关键字爆零）
B题：观察找规律（真的一点都不显然好吗！），发现题意理解错了···（不是自由落体QAQ）
C题：组合数取模，lucas用不上，因为模数太大了（自己真的菜，背不到代码还要去翻pdf）。
D题：是之前猴子捞月的翻版，考虑并查集反向连边，然而之前没有把那道题做了orz orz。

B题注意事项：这道题有一个很不显然的结论（为什么会很显然啊）就是从(0,0)出发，到(x,y)的最短距离为：（x+y）/2，但是这里就会考虑到推到过程，实际上就是先走(x-y)，然后跳y格，如果（x-y）与 y 不同奇偶就会出现要取上下整的情况，这个时候画画图（因为数学菜没法证明）就可以得到不同奇偶时的处理方法，还有一个就是最后算答案的时候，以及判断奇偶情况，都是根据（0，0）到（x，y）来判定的，这里很容易写错，判断奇偶可能会好理解，但是算答案的话就会有个疑问：为什么是根据(0,0)到目标水管，不是中间还有其他水管吗。我们可以这样抽象的想，就是前面讨论的水管是一定会通过的，通过了就假设不存在（因为对答案不会有影响，反正前一根水管道这根水管的距离是用来向上跳的，前面使用来保持平稳飞行的）

D题：这里引入一个很重要的思路，就是删繁就简，并查集由于只可增加不可删除，反向连边，判断连通块。

今天是进步的一天，我至少变成得70了···

今天又是菜鸡到爆的一天，两道签到题，一道都没拿到。
老规矩先记录一下今天比赛的优缺点：
优点1.准时换题，2.有按计划的去想题，也有自己的一些思路。
缺点：还是很慌，想到了正解，就没有去想反例（因为想正解就想了很久），做题有些中规中矩。也是经验不足，最后一道题有贪心和状压两种解法，但是都没有想到（虽然推了个方程但是都不知道自己错在哪里）。第一道题想出了正解的很小一部分，但是没有举反例，以为自己能A（还是太嫩了emmm）。

然后是算法时间：
A：100个堆。（对，就是100个堆）
B: 就是用前缀和，然后观察找规律，最后利用类似于dp的思想求解
C：要么性价比贪心，要么状态压缩。

个人发现，三道题前半段思路都跟我一样，但是我并没有想到后面半段，我个人的理解是刷题太少了，没有多少经验（前半段玩去了QAQ）我错了，我要反省QAQ。

几天没有更新啦，回来更新一下
2019.8.23练习赛

题目：(A)

Eyiz正在与邪恶的Dgdon战斗.
为了打败Dgdon,Eyiz决定召唤PhantasmDragon来帮助他.
但是,召唤PhantasmDragon需要搭建一个祭坛.祭坛可以视作一个的网格.网格从上往下数第行,从左往右数第列记作 .
现在,Eyiz在网格的每个格子中放置了三种字符中的一种,召唤出PhantasmDragon的数量取决于三种字符的排列方式.具体的,数量等于满足以下条件的有序四元组的数量.
条件: 位置上的字符为P, 位置上的字符为H, 位置上的字符为D.
Eyiz想知道一共能召唤出多少只PhantasmDragon.
算法：只需要差分一下，再加前缀和一下，再乘一下就可以啦

题目：（B）

自从周文武老师在班上吹嘘了"录试"这款游戏之后,PHD同学沉迷于其中无法自拔.
"录试"是这样一款游戏:两名玩家使用卡牌召唤随从进行战斗.每名随从具有攻击与血量两个属性,如果一名随从的血量<=0,它就会死亡.
PHD发现一张叫做考古专家雷诺的卡牌十分强大.它的攻击方式是,如果其攻击力为K,它会造成K次伤害,每次伤害为1,且会随机选择每次攻击的目标.现在,PHD同学想去挑战ZZY.他知道ZZY最喜欢使用的卡牌是奴隶主.奴隶主的血量为3,每当它受到伤害且没有死亡时,如果场上奴隶主数量不超过7,就会召唤另一个血量为3的奴隶主.我们假设场上只有雷诺与奴隶主,且雷诺只会攻击奴隶主.PHD想知道,在他的雷诺攻击结束之后,ZZY场上剩余奴隶主个数在模19260817意义下的期望值.

算法：这道题是一道递推+数学期望，然而我题目都没有看懂（当时特别的饿，然后我就开始颓废emm）
总结就是:要带够食物去比赛（乘法逆元有点忘记了要记得复习一下）

题目：（C）

你最近买六合彩赚了很多钱，导致一个银行账户存不下了，于是你开设了 i个账户，第 i个账户里存有 ai元。
你的好友们闻讯而来，纷纷要求兑现当时 ”苟富贵，勿相忘“ 的承诺，所以无可奈何的你只好把这些账户分给你的朋友们。
对于第 i个朋友，你会对应地把你开设的第 i个账户赠与他。但是，因为有些朋友已经多年不见，所以你并不想分很多钱给他们。
对于第 i个朋友，你只想分给他i元，但是第 i个账户里的钱可能并不与 bi相等。因此，你需要利用银行的转账系统来分配资金。
因为你 Too young, Sometimes naive, 你不小心选择了一个黑心银行。你的第个账户只能向第个账户转账。特别的，第个账户只能向第个账户转账。而且当第个账户向第个账户转账元时，需要等量地从第个账户中扣除元手续费。
请注意，每个账户不允许透支，也就是钱数不能小于0.
对于每个账户，只要没有透支，对转账额度和次数没有限制。
你想知道，有没有一种转账方案，使得你的计划得以实现，也就是第个账户的最终钱数等于 .
这道题是一道模拟（当然也可以公式过），但是有一个坑点就是可以试试数据2 2 1 2 1，正确答案是yes，但大部分程序会输出No原因是在a[i]-b[i]的时候要+1再除以二，如果结果大了，就再减一下，就可以通过了（很迷，真的emm）

最好的期望

1.【概率】搜集卡片

搜集卡片
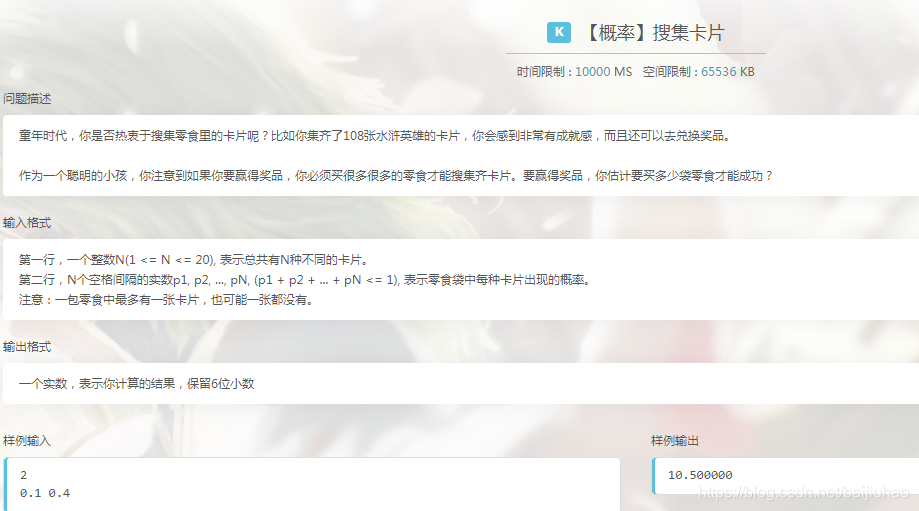
一道水题，卡了我半天，结果发现时不仅方程推错了，而且还是在用int进行计算emm
记录一下方程（感觉一道期望的部分都比较喜欢从后往前推）
$f[i]=f[i]*\displaystyle \sum^{1\to n}_{j}{p[j]}^{表示没有抽中任何卡片}+f[i]*\sum{p[j]}^{表示抽中了以前有过的卡片}+\sum{f[i|1<<j-1]*p[j]}^{表示抽中一张以前没有过的}+1$

2019.9.16
听董神说，这是一场可以用10minAK的比赛。然而，我全场暴力，还MLE了····

先总结：40+0+30=70（实际得分），期望得分：40+？+50=90+？（由于b题想到的感觉是正解但是不知道能得多少分（因为是在最后几分钟打的），C题给的是50分的暴力，但是只拿了30min）
然后是总结：发挥失误（更多的是在思维的发挥失误上面），代码上面大概是B题原地爆炸，有点失落。
在C题上面由于自己写代码的功底不足，改了1h，浪费了很多时间。A和B题本来是想到了正解的，但是，没有仔细的思考就忽略了正解，只能走暴力或者其他的歪门邪道。关于B题有贪心的策略在里面，但是我一看到Dp就不敢用贪心。然后方程没有得到优化，就没这么写。（感觉在贪心和Dp的分别上面我一直存在很大的问题）

2019.9.18
热烈庆贺我的爆零赛，多久没打了。A题以为是板题，然后就挂掉了。正解是贝尔曼·福特。（woc！这谁想得出来啊）这解法我是打了几百年都见不到的算法吧。B题，我花了1h半想出了正解的一半，然后我就剩下30min敲正解了。C题，我一来就想到了Dp，但是并不是，正解是滑动窗口emm