2.1数据的表示和存储(一）

2.1 数制和编码

1.信息的二进制编码

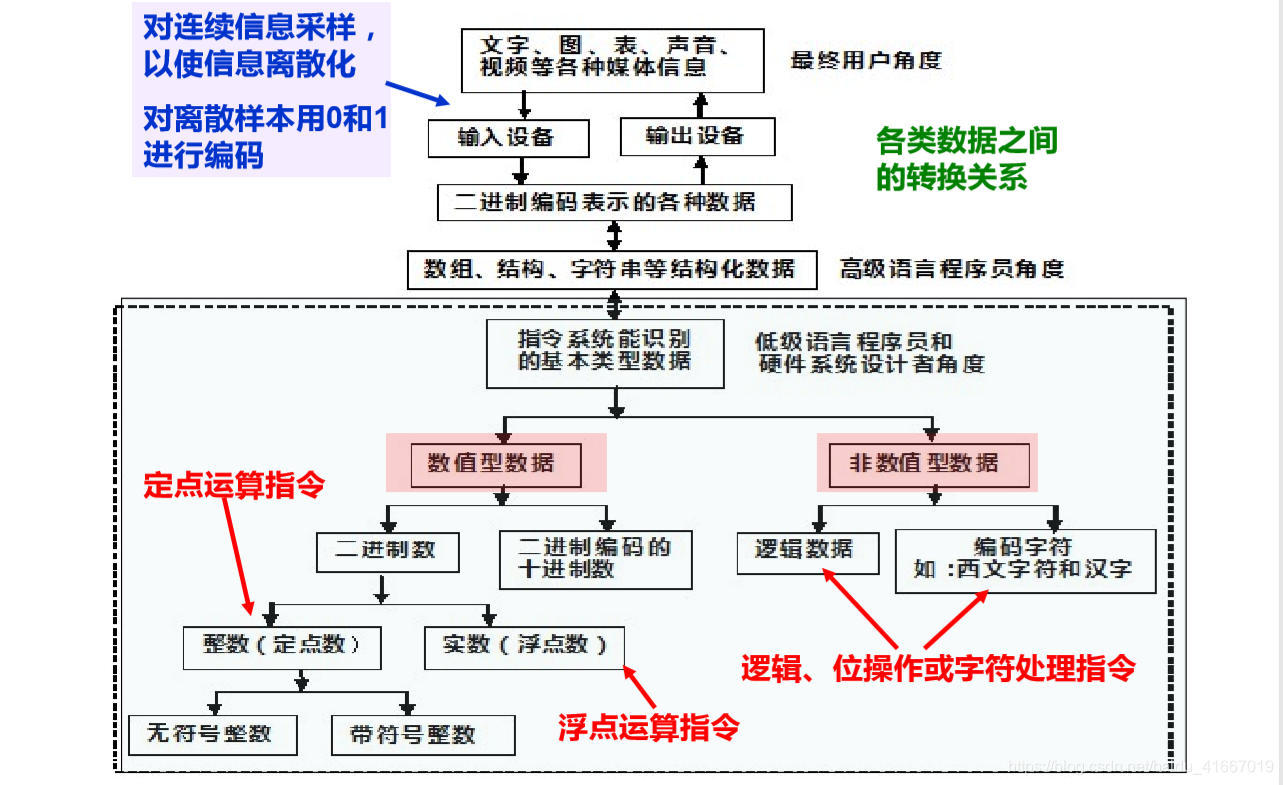
（1） 机器级数据分两大类

• 数值数据：无符号整数、带符号整数、浮点数（实数）
• 非数值数据：逻辑数（包括位串）、西文字符和汉字

（2）计算机内部所有信息都用二进制（即：0和1）进行编码

• 用二进制编码的原因
   ①制造二个稳定态的物理器件容易(电位高/低，脉冲有/无，正/负极)
   ②二进制编码、计数、运算规则简单
   ③正好与逻辑命题真/假对应，便于逻辑运算
   ④可方便地用逻辑电路实现算术运算
• 真值和机器数
   机器数：用0和1编码的计算机内部的0/1序列
   真值：真正的值，即：现实中带正负号的数

2.数值数据的表示

（1）数值数据表示的三要素

• 进位计数制
• 定、浮点表示
• 如何用二进制编码 即：要确定一个数值

即：要确定一个数值数据的值必须先确定这三个要素。
例如，20137564的值是多少？ 答案是：不知道

（2）进位计数制

• 十进制、二进制、十六进制、八进制数及其相互转换

（3）定/浮点表示（解决小数点问题）

• 定点整数、定点小数
• 浮点数（可用一个定点小数和一个定点整数来表示）

（4）定点数的编码（解决正负号问题）

• 原码、补码、反码、移码（反码很少用）

3.进制计数制

(1) R进位计数制

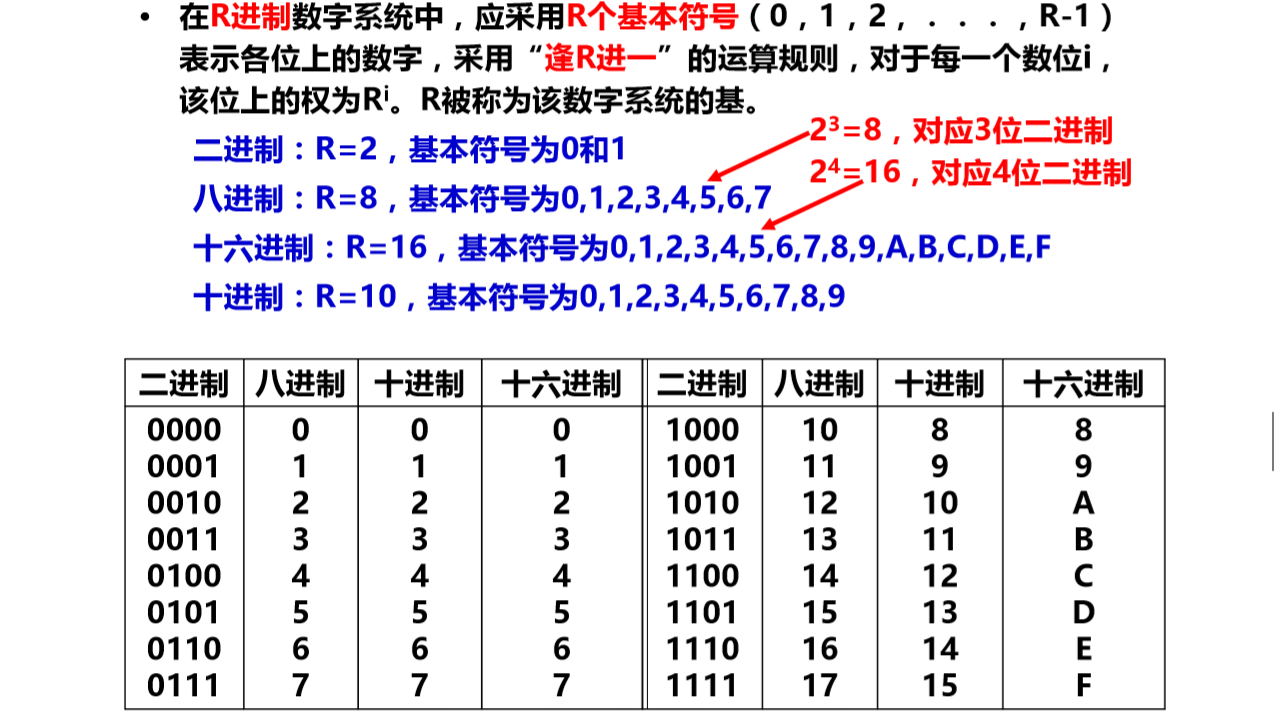
• 八进制/ 十六进制是二进制的简便表示。便于阅读和书写！它们之间对应简单，转换容易。
• 在机器内部用二进制表示，在屏幕或其他设备上表示时，转换为八进制/十六进制数，可缩短长度。
    八进制：Octal （用后缀“O”表示）
    十六进制：Hexadecimal （用后缀“H”，或前缀“0x”表示）
• 现代计算机系统多用十六进制表示机器数

(2) 十进制数与R进制数之间的转换

整数----“除基取余，上右下左” 小数----“乘基取整，上左下右”

(3) 十进制数与二进制数之间的转换

整数----“除基取余，上右下左” 小数----“乘基取整，上左下右”

(4) 十进制数与八进制数之间的转换

整数----“除基取余，上右下左” 小数----“乘基取整，上左下右”
（可能小数部分总得不到0，此时得到一个近似值 ）

4. 定点数和浮点数

2.2 定点数的编码表示

1. 原码表示

“正”号用0表示 “负”号用1表示，数值部分不变

Decimal	Binary	Decimal	Binary
0	0000	-0	1000
1	0001	-1	1001
2	0010	-2	1010
3	0011	-3	1011
4	0100	-4	1100
5	0101	-5	1101
6	0110	-6	1110
7	0111	-7	1111

易于理解，但是：

 ① 0 的表示不唯一，故不利于程序员编程
 ② 加、减运算方式不统一
 ③ 需额外对符号位进行处理，故不利于硬件设计
 ④ 特别当a小于b时，实现a-b比较困难

2. 补码表示

(1) 模运算（modular运算）

• 重要概念：在一个模运算系统中，一个数与它除以“模”后的余数等价

                    时钟是一种模12系统 
    假定钟表时针指向10点，要将它拨向6点， 则有两种拨法： 
        ①倒拨4格：10-4 = 6
        ②顺拨8格：10+8 = 18 ≡ 6(mod 12) 
    模12系统中： 10-4 ≡10+8(mod 12) -4 ≡8(mod 12)    
    则，称8是-4对模12的补码（即：-4的模12补码等于8）。
    同样有-3 ≡9（mod 12） -5 ≡ 7（mod 12）等
  

结论1：一个负数的补码等于模减该负数的绝对值
结论2：对于某一确定的模，某数减去小于模的另一数，总可以用该数加上另一数负数的补码来代替。

(2) 补码的表示

补码（modular运算）：+ 和–的统一

• 补码的定义 : [X]补= 2n + X （-2n≤X＜2n，mod 2n）,其中X是真值，[x]补是机器数

• 求特殊数的补码

    假定机器数有n位
    ①[-2n-1]补= 2n -2n-1 = 10…0（n-1个0）（mod 2n）
    ②[-1]补= 2n -0…01 = 11…1（n个1） （mod 2n）
    ③[+0]补= [-0]补= 00…0（n个0） 
  

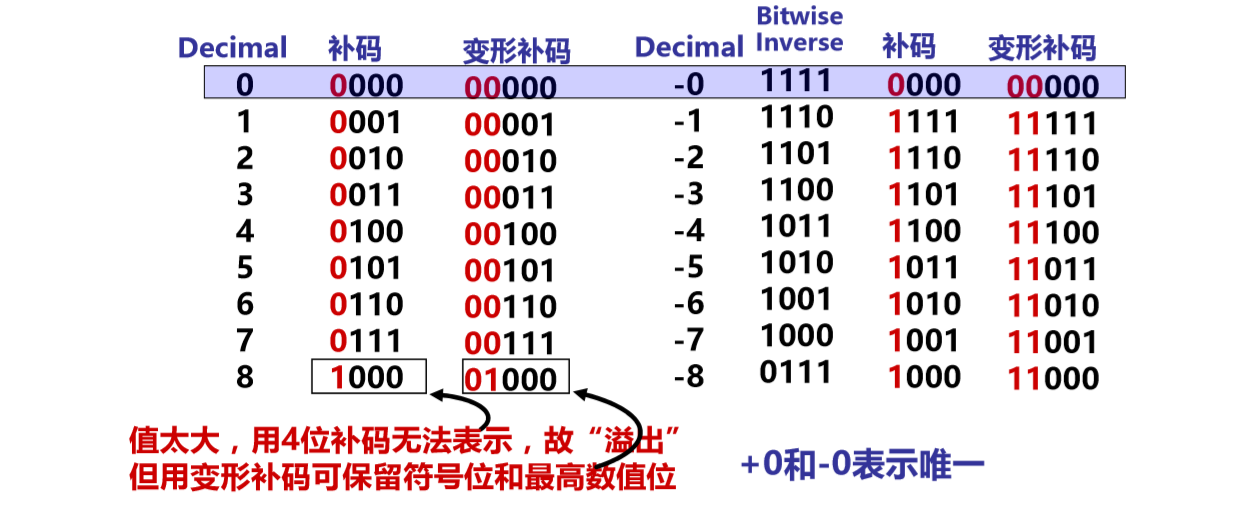
(3) 变形补码的表示

补码定义：[X]补= 2n + X （-2n≤X＜2n，mod 2n）
变形（4’s）补码：双符号，用于存放可能溢出的中间结果。

• 正数：符号位（sign bit）为0，数值部分不变
• 负数：符号位为1，数值部分“各位取反，末位加1”
• +0和-0表示唯一

（4）求真值的补码

（5）求补码的真值

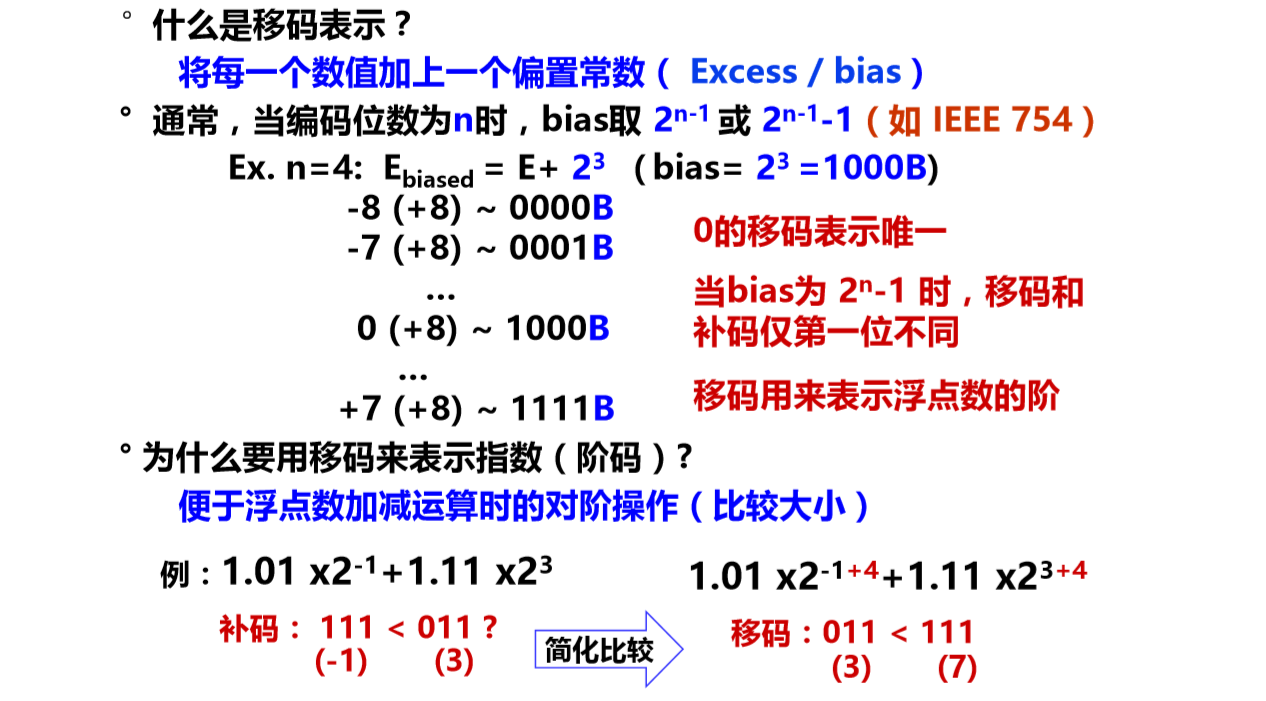
3. 移码表示Excess (biased) notion

2.3 C语言中的整数

1. 无符号整数 (Unsigned integer)

常在一个数的后面加一个“u”或“U”表示无符号数

（1）最低有效位&最低有效位

• 机器中字的位排列顺序有两种方式：（例：32位字:0…010112）
  • 高到低位从左到右：00000000000000000000000000001011 <==LSB
  • 高到低位从右到左：11010000000000000000000000000000 <==MSB
• Leftmost和rightmost这两个词有歧义，故用LSB(Least SignificantBit)来表示最低有效位，用MSB来表示最高有效位
• 高位到低位多采用从左往右排列

（2）无符号整数

• 一般在全部是正数运算且不出现负值结果的场合下，可使用无符号 数表示。例如，地址运算，编号表示，等等
• 无符号整数的编码中没有符号位
• 能表示的最大值大于位数相同的带符号整数的最大值（例如，8位无符号整数最大是255（11111111） 而8位带符号整数最大为127（01111111） ）

2. 带符号整数（Signed integer）

计算机必须能处理正数(positive) 和负数(negative)，用 MSB表示数符（0–正数，1–负数）

• 有三种定点编码方式
    Signed and magnitude （原码）
    Excess (biased) notion （移码）
    Two’s complement （补码）
• 50年代以来，所有计算机都用补码来表示带符号整数 （原因）
    ①补码运算系统是模运算系统，加、减运算统一
    ②数0的表示唯一，方便使用
    ③比原码多表示一个最小负数

3. C语言中的整数

若同时有无符号和带符号整数，则C编译器将带符号整数强制转换为无符号数，符号与数值分开进行处理
通过补码进行整数的大小比较

例一

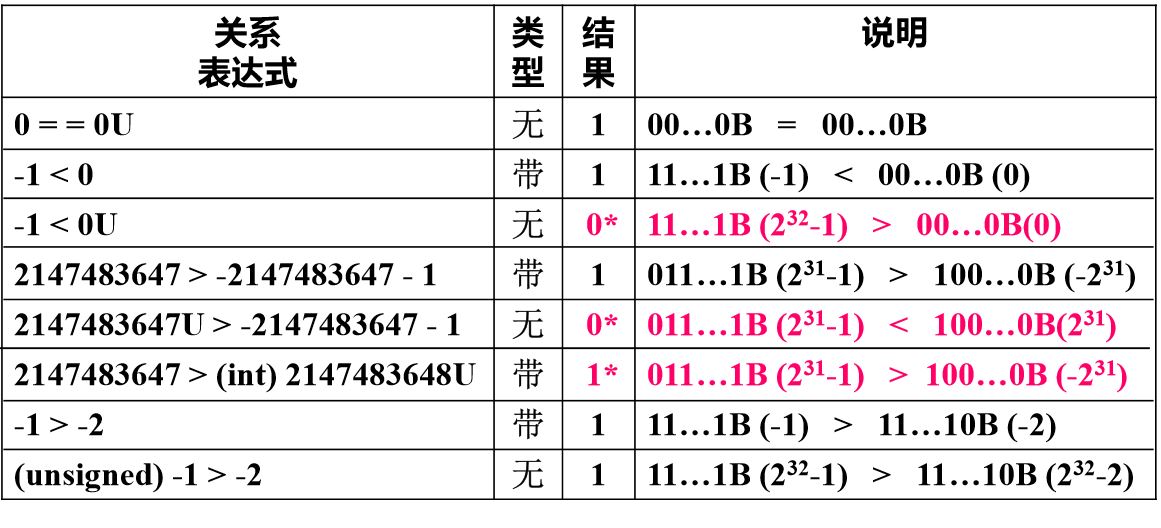
例二

//考虑以下C代码： 
	int x = –1; 
	unsigned u = 2147483648; 
	printf ( “x = %u = %d\n”, x, x); 
	printf ( “u = %u = %d\n”, u, u); 
//在32位机器上运行上述代码时，它的输出结果:
// x = 4294967295 = –1
// u = 2147483648 = –2147483648 

• –1的补码整数表示为“11…1”，作为32位无符号数解释 时，其值为232–1= 4 294 967 296–1 = 4 294 967 295。
• 231的无符号数表示为“100…0”，被解释为32位带符号整数 时，其值为最小负数：–232-1= –231= –2 147 483 648。

编译器处理常量时默认的类型

• C90

  范围	类型
  0 ~ 2^31-1	int
  2^31 ~ 2^32-1	unsigned int
  2^32 ~ 2^63-1	long long
  2^63 ~ 2^64-1	unsigned long long

• C99

  范围	类型
  0~2^31-1	int
  2^31 ~ 2^63-1	long long
  2^63 ~ 2^64-1	unsigned long long

• 2147483648=2^31

Q&A

Q1: 在有些32位系统上，C表达式-2147483648 < 2147483647的执行结 果为false。Why？
A1: 在ISO C90标准下，2147483648为unsigned int型，因此 “-2147483648 < 2147483647”按无符号数比较， 10……0B比01……1B大，结果为false。在ISO C99标准下，“-2147483648 < 2147483647”按带符号整数比较， 10……0B比01……1B小，结果为true。

Q2: 若定义变量“int i=-2147483648;”，则“i < 2147483647”的执行 结果为true。Why？
A2： i < 2147483647 按int型数比较，结果为true。

Q3: 如果将表达式写成“-2147483647-1 < 2147483647”，则结果会怎 样呢？Why？
A3: -2147483647-1 < 2147483647 按int型比较，结果为true。