Transformer中的位置编码：绝对位置编码、相对位置编码与旋转位置编码

1. 引言

Transformer模型自2017年提出以来，凭借其在序列到序列任务中的优异表现，迅速成为自然语言处理（NLP）领域的主流模型。与传统的循环神经网络（RNN）不同，Transformer模型完全基于自注意力机制，因此在处理长距离依赖关系方面有显著优势。然而，由于Transformer模型缺乏内置的序列顺序信息，必须通过位置编码（Positional Encoding）显式引入位置信息，以便模型能够区分序列中的不同位置。

位置编码是Transformer模型中一个至关重要的部分，直接影响到模型对序列信息的处理能力。 本文将系统地介绍Transformer模型中的三种主要位置编码方法：绝对位置编码、相对位置编码和旋转位置编码。通过对这些方法的详细剖析，并结合具体代码和案例，深入探讨它们在实际应用中的表现和适用场景。

在本文的案例部分，我们将以“我爱你，中国。”为例，使用d_model=32的设定，通过代码展示每种位置编码的实际效果，以帮助读者更直观地理解这些编码方法。

2. 绝对位置编码

2.1 绝对位置编码的原理

绝对位置编码（Absolute Positional Encoding）是最常见的一种位置编码方法，其**思想是在每个输入序列的元素上添加一个位置向量，以表示该元素在序列中的具体位置。****这个位置向量通常通过固定的函数生成，与输入数据无关。**通常使用的是正弦和余弦函数，这样生成的编码具有很强的周期性，能够捕捉序列中的相对位置信息。

具体来说，对于序列中的第𝑝𝑜𝑠个位置，绝对位置编码向量的第𝑖个维度的值定义如下：

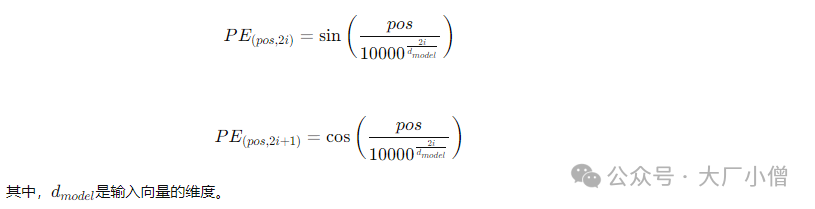
2.2 绝对位置编码的代码实现

接下来，我们将展示如何在代码中实现绝对位置编码，并以“我爱你，中国。”为例，展示位置编码后的向量表示。

import numpy as np
import matplotlib.pyplot as plt

def get_absolute_positional_encoding(seq_len, d_model):
    position = np.arange(seq_len)[:, np.newaxis]    
    div_term = np.exp(np.arange(0, d_model, 2) * -(np.log(10000.0) / d_model))    
    pe = np.zeros((seq_len, d_model))    
    pe[:, 0::2] = np.sin(position * div_term)    
    pe[:, 1::2] = np.cos(position * div_term)    
    return pe

# 假设句子长度为8，d_model为32
sentence = "我爱你，中国。"
seq_len = len(sentence)
d_model = 32

absolute_positional_encoding = get_absolute_positional_encoding(seq_len, d_model)

# 展示绝对位置编码的效果
plt.figure(figsize=(12, 8))
plt.imshow(absolute_positional_encoding, cmap='viridis')
plt.colorbar()
plt.title("Absolute Positional Encoding")
plt.xlabel("d_model dimensions")
plt.ylabel("Position in Sentence")
plt.show()

2.3 案例分析

在上面的代码中，我们为长度为8的句子生成了一个绝对位置编码矩阵。该矩阵的维度为（8, 32），每一行表示句子中一个位置的编码。通过热图可以看到，不同位置的编码在特定维度上具有不同的模式，这些模式帮助Transformer区分序列中不同位置的元素。

具体到“我爱你，中国。”这句话，每个字符都有一个32维的编码向量，这个向量的数值是基于该字符的位置计算出来的。这样，Transformer模型在处理这个句子时，就可以感知到每个字符在句子中的位置。

2.4 绝对位置编码的优缺点

绝对位置编码的优势在于其简单且具有良好的可解释性。 它能够有效地为序列中的每个位置分配独特的编码，从而帮助模型捕捉序列的顺序信息。然而，它也有一定的**局限性，**尤其是在处理变长序列或长距离依赖时，绝对位置编码可能无法充分表达复杂的位置信息。

3. 相对位置编码

相对位置编码最早在Transformer-XL和T5等模型中引入，以解决绝对位置编码在捕捉长距离依赖关系时的不足。

3.1 相对位置编码的原理

与绝对位置编码不同，相对位置编码（Relative Positional Encoding）并不直接为每个位置分配一个唯一的编码，而是关注序列中各元素之间的相对位置。 相对位置编码的**核心思想是通过计算序列中元素之间的距离，来表示它们之间的相对关系。这种方法尤其适合处理需要捕捉长距离依赖关系的任务，因为它能够更加灵活地表示序列中的结构信息。

相对位置编码可以通过多种方式**实现，其中最常用的方法之一是将位置差值与注意力权重相结合，即在计算自注意力时，不仅考虑内容，还考虑位置差异。**这样，模型能够根据元素之间的距离调整它们之间的交互强度。

3.2 公式推导出

3.2.1 基本概念

3.1.2 计算Attention Scores

在这里，我们可以看到相对位置编码引入了额外的偏置项和位置信息，通过这种方式捕捉到序列中的长距离依赖关系。

3.3 案例

3.4 相对位置编码的代码实现

下面是一个简单的相对位置编码的实现示例，仍然以“我爱你，中国。”为例。

import torch
import torch.nn.functional as F

class RelativePositionalEncoding(torch.nn.Module):
    def __init__(self, d_model, max_len=5000):     
        super(RelativePositionalEncoding, self).__init__()        
        self.d_model = d_model        
        self.max_len = max_len        
        
        # 生成相对位置编码        
        self.relative_positions_matrix = self.generate_relative_positions_matrix(max_len)        
        self.embeddings_table = self.create_embeddings_table(max_len, d_model)    
        
    def generate_relative_positions_matrix(self, length):    
        range_vec = torch.arange(length)        
        distance_mat = range_vec[None, :] - range_vec[:, None]        
        return distance_mat    
        
    def create_embeddings_table(self, max_len, d_model):    
        table = torch.zeros(max_len, max_len, d_model)        
        for pos in range(-max_len+1, max_len):        
            table[:, pos] = self.get_relative_positional_encoding(pos, d_model)        
        return table    
        
    def get_relative_positional_encoding(self, pos, d_model):   
        pos_encoding = torch.zeros(d_model)        
        for i in range(0, d_model, 2):         
            pos_encoding[i] = torch.sin(pos / (10000 ** ((2 * i)/d_model)))            
            if i + 1 < d_model:           
                pos_encoding[i + 1] = torch.cos(pos / (10000 ** ((2 * i)/d_model)))        
        return pos_encoding    
        
    def forward(self, length):    
        positions_matrix = self.relative_positions_matrix[:length, :length]        
        return F.embedding(positions_matrix, self.embeddings_table)

# 使用相对位置编码
sentence_length = len(sentence)
relative_positional_encoding = RelativePositionalEncoding(d_model, max_len=sentence_length)
relative_positional_encodings = relative_positional_encoding(sentence_length)

# 展示相对位置编码的效果
plt.figure(figsize=(12, 8))
plt.imshow(relative_positional_encodings.detach().numpy(), cmap='viridis')
plt.colorbar()
plt.title("Relative Positional Encoding")
plt.xlabel("d_model dimensions")
plt.ylabel("Relative Position")
plt.show()

3.5 案例分析

在这个示例中，我们生成了一个基于相对位置的编码矩阵，该矩阵的维度为（8, 8, 32），每个元素表示句子中两个位置之间的相对编码向量。这种编码方式在处理长句子时能够更好地捕捉不同元素之间的关系，因为它可以灵活地处理序列中的相对位置。

例如，在“我爱你，中国。”中，模型可以更准确地捕捉到“我”和“爱”，“爱”和“你”之间的关系，而不仅仅依赖于它们在句子中的绝对位置。

3.6 相对位置编码的优缺点

相对位置编码的优势在于其对序列长度和相对位置信息的良好适应性，特别适合处理长文本或存在复杂依赖关系的任务。然而，相对位置编码的实现相对复杂，且在某些情况下可能增加计算成本。

4. 旋转位置编码

4.1 旋转位置编码的原理

旋转位置编码（Rotary Positional Encoding, RoPE）是近年来提出的一种新型位置编码方法，主要应用于图像处理和三维数据处理中。RoPE的核心思想是通过对输入向量进行旋转变换，将位置信息嵌入到向量中。具体来说，RoPE通过旋转每个维度对中的向量，实现对序列中位置信息的编码。

RoPE具有很强的表达能力，尤其是在处理具有对称性或周期性的任务时，能够更加自然地捕捉序列中的位置信息。

4.2 公式推导

4.2.1 基本概念

4.2.2 在查询和键向量中的应用

4.2.3 旋转操作 (rotate) 详解

可以得到：

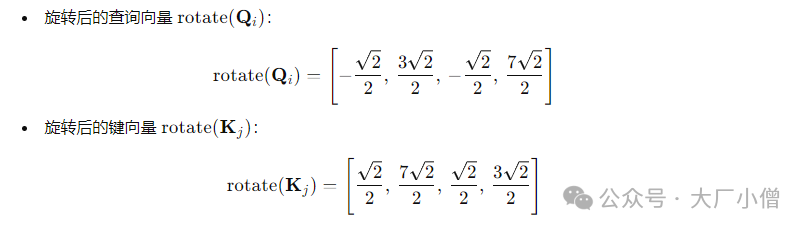
4.3 旋转位置编码的代码实现

下面的代码展示了如何在NLP任务中实现旋转位置编码，并以“我爱你，中国。”为例，展示其效果。

4.4 案例分析

在上述代码中，我们通过旋转向量对实现了RoPE编码，并将其应用于Q和K矩阵。可视化结果显示，经过旋转位置编码后，Q矩阵的不同维度展示出明显的周期性模式，这有助于捕捉序列中的周期性或对称性信息。

在“我爱你，中国。”的例子中，RoPE能够更好地捕捉句子中的重复模式和相似结构。例如，“我”和“你”可能在某些情境中具有相似的语义，而这种关系可以通过RoPE更自然地表达。

4.5 旋转位置编码的优缺点

RoPE的优势在于其强大的表达能力，特别是在处理具有对称性或周期性特征的数据时表现优异。 此外，RoPE具有一定的灵活性，可以应用于不同类型的输入数据。然而，RoPE的实现复杂度较高，且其适用性尚需在更多场景中验证。

5. 三种位置编码的比较与应用场景

5.1 性能比较

在实际应用中，选择适当的编码方式对于模型性能至关重要。绝对位置编码因其简单易实现且在大多数NLP任务中表现良好，成为默认选择。然而，在处理长文本或复杂依赖关系时，相对位置编码具有明显优势，能够捕捉到更为细致的序列信息。而RoPE则因其在特定任务中的独特表现，成为研究人员探索的热点。

5.2 应用场景

绝对位置编码：适用于大多数NLP任务，尤其是短文本处理和无复杂依赖的场景，如文本分类和情感分析。

相对位置编码：适用于长文本处理和需要捕捉长距离依赖的任务，如机器翻译和问答系统。

旋转位置编码：适用于具有对称性或周期性特征的数据处理任务，如图像处理、时间序列分析，以及在3D数据中的应用。

6. 总结

位置编码是Transformer模型中至关重要的一部分，不同的编码方式适用于不同的任务和数据类型。本文详细介绍了绝对位置编码、相对位置编码和旋转位置编码的原理、实现及应用，通过具体的案例分析展示了它们在实际任务中的表现。随着NLP领域的不断发展，新的位置编码方法可能会不断涌现，进一步提升Transformer模型在复杂任务中的表现。

了解并掌握这些位置编码方法，将有助于研究人员和工程师更好地应用Transformer模型，处理各种序列数据，提升模型的性能和应用效果。

如何学习大模型 AI ？

由于新岗位的生产效率，要优于被取代岗位的生产效率，所以实际上整个社会的生产效率是提升的。

但是具体到个人，只能说是：

“最先掌握AI的人，将会比较晚掌握AI的人有竞争优势”。

这句话，放在计算机、互联网、移动互联网的开局时期，都是一样的道理。

我在一线互联网企业工作十余年里，指导过不少同行后辈。帮助很多人得到了学习和成长。

我意识到有很多经验和知识值得分享给大家，也可以通过我们的能力和经验解答大家在人工智能学习中的很多困惑，所以在工作繁忙的情况下还是坚持各种整理和分享。但苦于知识传播途径有限，很多互联网行业朋友无法获得正确的资料得到学习提升，故此将并将重要的AI大模型资料包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。

😝有需要的小伙伴，可以Vx扫描下方二维码免费领取🆓

👉1.大模型入门学习思维导图👈

要学习一门新的技术，作为新手一定要先学习成长路线图，方向不对，努力白费。

对于从来没有接触过AI大模型的同学，我们帮你准备了详细的学习成长路线图&学习规划。可以说是最科学最系统的学习路线，大家跟着这个大的方向学习准没问题。（全套教程文末领取哈）

👉2.AGI大模型配套视频👈

很多朋友都不喜欢晦涩的文字，我也为大家准备了视频教程，每个章节都是当前板块的精华浓缩。

👉3.大模型实际应用报告合集👈

这套包含640份报告的合集，涵盖了AI大模型的理论研究、技术实现、行业应用等多个方面。无论您是科研人员、工程师，还是对AI大模型感兴趣的爱好者，这套报告合集都将为您提供宝贵的信息和启示。（全套教程文末领取哈）

👉4.大模型落地应用案例PPT👈

光学理论是没用的，要学会跟着一起做，要动手实操，才能将自己的所学运用到实际当中去，这时候可以搞点实战案例来学习。（全套教程文末领取哈）

👉5.大模型经典学习电子书👈

随着人工智能技术的飞速发展，AI大模型已经成为了当今科技领域的一大热点。这些大型预训练模型，如GPT-3、BERT、XLNet等，以其强大的语言理解和生成能力，正在改变我们对人工智能的认识。 那以下这些PDF籍就是非常不错的学习资源。

👉6.大模型面试题&答案👈

截至目前大模型已经超过200个，在大模型纵横的时代，不仅大模型技术越来越卷，就连大模型相关的岗位和面试也开始越来越卷了。为了让大家更容易上车大模型算法赛道，我总结了大模型常考的面试题。

这份完整版的大模型 AI 学习资料已经上传优快云，朋友们如果需要可以微信扫描下方优快云官方认证二维码免费领取【保证100%免费】

😝有需要的小伙伴，可以Vx扫描下方二维码免费领取🆓