matlab/两方三方四方演化博弈建模、方程求解、相位图、雅克比矩阵、稳定性分析。 2.Mat

关于Matlab与演化博弈建模的深入探讨

一、引言

演化博弈论是一种基于博弈理论的研究方法，常用于描述复杂的动态和参与者之间的互动关系。Matlab作为一款强大的科学计算，在演化博弈建模方面有着广泛的应用。本文将详细介绍使用Matlab进行两方、三方、四方演化博弈建模的流程，包括方程求解、相位图、雅克比矩阵稳定性分析等关键步骤。

二、两方、三方、四方演化博弈建模

1. 模型构建：根据具体的博弈场景，设定参与者的策略空间、收益函数等。
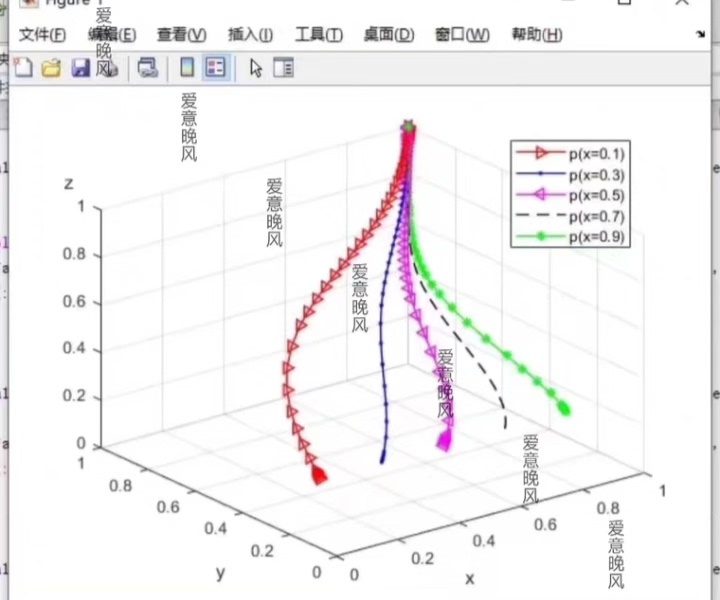
2. 方程求解：通过设定演化方程，利用Matlab的数值计算能力求解各参与者的演化路径。
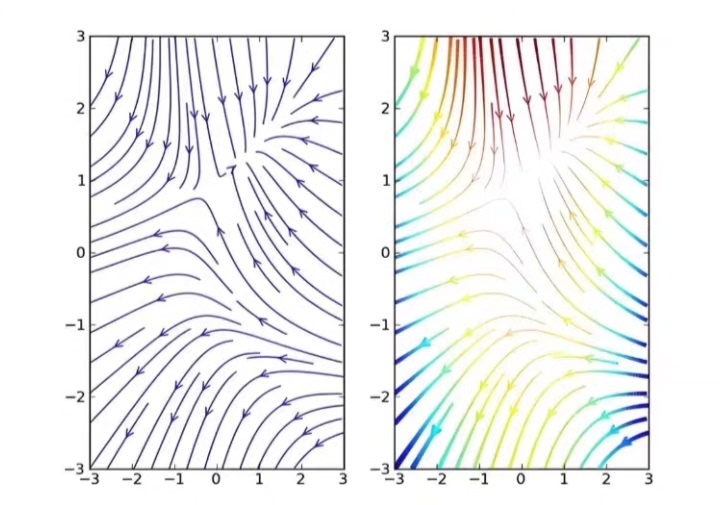
3. 相位图：根据求解结果，绘制相位图，直观地展示的动态变化过程。

三、方程求解与稳定性分析

1. 雅克比矩阵：通过计算雅克比矩阵，分析的局部稳定性。雅克比矩阵的元素由演化方程的偏导数组成。
2. 稳定性分析：根据雅克比矩阵的特征值，判断的稳定性。若所有特征值的实部均小于零，则为稳定状态。

四、Matlab数值仿真模拟

1. 参数赋值：根据实际需求，为模型参数赋值。
2. 初始演化路径：设定初始条件，观察的演化路径。
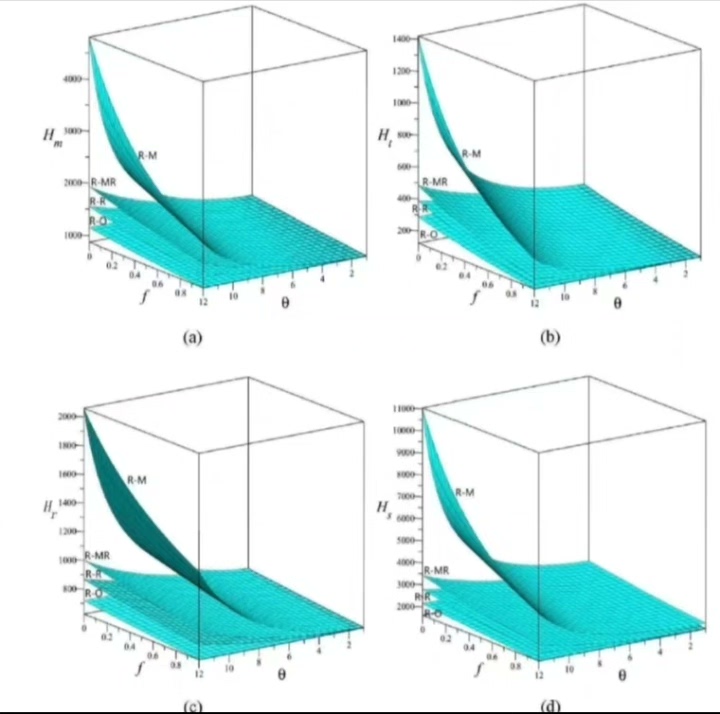
3. 参数敏感性：通过改变参数值，分析参数对演化的影响，以及的参数敏感性。

五、含有动态奖惩机制的演化稳定性控制

1. 线性动态奖惩：通过设定线性奖惩机制，调整参与者的收益，从而影响的演化方向。
2. 非线性动态奖惩：在某些复杂场景下，可能需要采用非线性的奖惩机制，以更精细地控制的演化过程。
3. 稳定性控制：通过调整奖惩机制，使达到期望的稳定状态。

六、Vensim PLE动力学（SD）模型的演化博弈仿真

1. 因果逻辑关系：在Vensim PLE中，建立模型的因果逻辑关系，设定各变量之间的相互影响。
2. 流量存量图：绘制流量存量图，描述内部的流动和存储关系。
3. 模型调试：通过反复调试模型参数，使模型更准确地反映实际的演化过程。

七、结论

本文详细介绍了使用Matlab进行演化博弈建模的流程和方法，包括两方、三方、四方演化博弈建模、方程求解、相位图、雅克比矩阵稳定性分析等关键步骤。同时，还介绍了Matlab数值仿真模拟、含有动态奖惩机制的演化稳定性控制以及Vensim PLE动力学（SD）模型的演化博弈仿真等方法。这些方法可以帮助我们更好地理解复杂的演化过程，为实际问题的解决提供有力的工具。
matlab/两方三方四方演化博弈建模、方程求解、相位图、雅克比矩阵、稳定性分析。
2.Matlab数值仿真模拟、参数赋值、初始演化路径、参数敏感性。
3.含有动态奖惩机制的演化稳定性控制，线性动态奖惩和非线性动态奖惩。
4.Vensim PLE动力学（SD）模型的演化博弈仿真，因果逻辑关系、流量存量图、模型调试等