DAY 14 SHAP库的绘制

原创已于 2025-05-29 21:02:40 修改 · 1.3k 阅读

CC 4.0 BY-SA版权

文章标签：

于 2025-05-29 21:01:41 首次发布

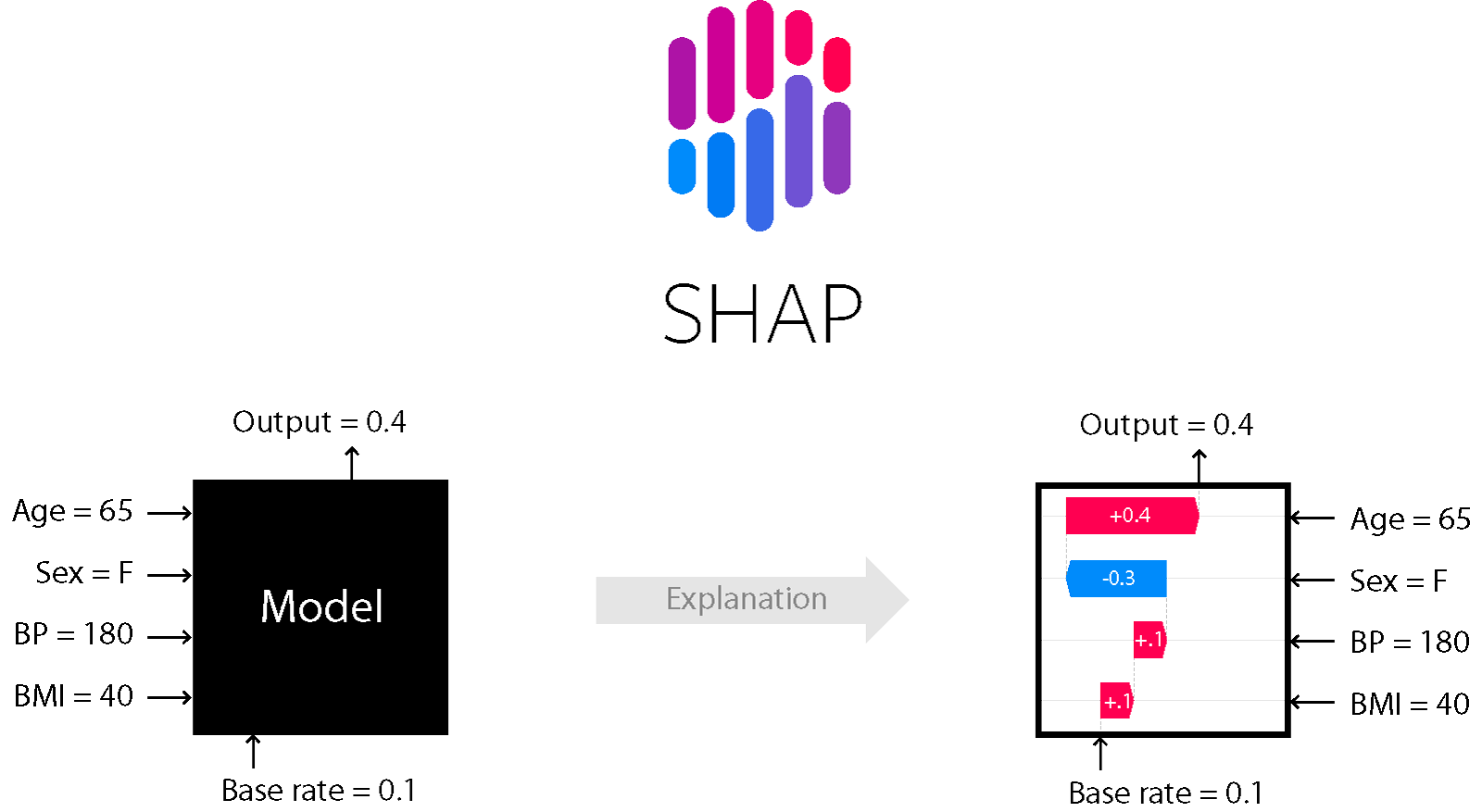
上面这个图就是一个比较直观的解释。机器学习模型一般都是一个黑盒。比如某个模型要进行一些预测任务，首先对模型输入一些已知条件（Age=65,Sex=F,BP=180,BMI=40），然后模型根据输入进行训练，最终训练完的模型可以对该条件输出预测结果（Output=0.4）。

所以这样模型只能得到最终的结果，至于模型内部是怎么计算的，输入的已知条件（Age=65,Sex=F,BP=180,BMI=40）是怎么对预测结果（Output=0.4）影响的，我们都没法知道。而SHAP模型就可以让我们知道这些已知条件到底对最终预测结果起到哪些影响（是对结果起到正向影响还是对结果起到了负向影响）。

SHAP 属于模型事后解释的方法，它的核心思想是计算特征对模型输出的边际贡献，再从全局和局部两个层面对“黑盒模型”进行解释。SHAP构建一个加性的解释模型，所有的特征都视为“贡献者”。

一、SHAP

SHAP的全称是SHapley Additive exPlanation，SHAP是由Shapley value启发的可加性解释模型。而Shapley value起源于合作博弈论，那什么是合作博弈呢。比如说甲乙丙丁四个工人一起打工，甲和乙完成了价值100元的工件，甲、乙、丙完成了价值120元的工件，乙、丙、丁完成了价值150元的工件，甲、丁完成了价值90元的工件，那么该如何公平、合理地分配这四个人的工钱呢？Shapley提出了一个合理的计算方法，我们称每个参与者分配到的数额为Shapley value。

结合文章一开始提到的预测任务，我认为就是已知条件（Age=65,Sex=F,BP=180,BMI=40）一起完成了预测结果（Output=0.4），那么该如何公平、合理地分配这四个已知条件对预测结果的贡献呢？此时SHAP模型就会给这四个已知条件都分配一个Shapley value值，根据这个值我们就可以很好的进行理解。

二、SHAP 原理简介

目标： 理解复杂机器学习模型（尤其是“黑箱”模型，如随机森林、梯度提升树、神经网络等）为什么会对特定输入做出特定预测。SHAP 提供了一种统一的方法来解释模型的输出。

核心思想：合作博弈论中的 Shapley 值

SHAP （SHapley Additive exPlanations）的核心基于博弈论中的 Shapley 值概念。想象一个合作游戏：

玩家（Players）： 模型的特征（Features） 就是玩家。
游戏（Game）： 目标是预测某个样本的输出值。
合作（Coalition）： 不同的特征子集可以“合作”起来进行预测。
奖励/价值（Payout/Value）： 某个特征子集进行预测得到的值。
目标： 如何公平地将最终预测结果（相对于平均预测结果的“收益”）分配给每个参与的特征（玩家）？

Shapley 值的计算思路（概念上）：

为了计算一个特定特征（比如“特征 A”）对某个预测的贡献（它的 Shapley 值），SHAP 会考虑：

所有可能的特征组合（子集/联盟）： 从没有特征开始，到包含所有特征。
特征 A 的边际贡献： 对于每一个特征组合，比较“包含特征 A 的组合的预测值”与“不包含特征 A 但包含其他相同特征的组合的预测值”之间的差异。这个差异就是特征 A 在这个特定组合下的“边际贡献”。
加权平均：Shapley 值是该特征在所有可能的特征组合中边际贡献的加权平均值。权重确保了分配的公平性。

SHAP 的关键特性（加性解释 - 加法解释）：

SHAP 的一个重要特性是**加性（Additive）**。这意味着：

基准值（Base Value / Expected Value）： 这是模型在整个训练（或背景）数据集上的平均预测输出。可以理解为没有任何特征信息时的“默认”预测。
SHAP 值之和： 对于任何一个样本的预测，所有特征的 SHAP 值加起来，再加上基准值，就精确地等于该样本的模型预测值。
```
模型预测值(样本 X) = 基准值 + SHAP值(特征1) + SHAP值(特征2) + ... + SHAP值(特征N)
```

为什么会生成 shap_values 数组？

根据上述原理，SHAP 需要为每个样本的每个特征计算一个贡献值（SHAP 值）：

解释单个预测：SHAP 的核心是解释单个预测结果。
特征贡献： 对于这个预测，我们需要知道每个特征是把它往“高”推了，还是往“低”推了（相对于基准值），以及推了多少。
数值化： 这个“推力”的大小和方向就是该特征对该样本预测的 SHAP 值。

因此：

对于回归问题：
- 模型只有一个输出。
- 对个样本中的每一个，计算个特征各自的 SHAP 值。n_samplesn_features
- 这就自然形成了形状为的数组。代表第个样本的第个特征对该样本预测值的贡献。(n_samples, n_features)shap_values[i, j]ij
对于分类问题：
- 模型通常为每个类别输出一个分数或概率。
- SHAP 需要解释模型是如何得到每个类别的分数的。
- 因此，对个样本中的每一个，分别为每个类别计算个特征的 SHAP 值。n_samplesn_features
- 最常见的组织方式是返回一个列表，列表长度等于类别数。列表的第个元素是一个的数组，表示所有样本的所有特征对预测类别 k 的贡献。k(n_samples, n_features)
- shap_values[k][i, j]代表第个样本的第个特征对该样本预测类别 k 的贡献。ij

总结:

SHAP 通过计算每个特征对单个预测（相对于平均预测）的边际贡献（Shapley 值），提供了一种将模型预测分解到每个特征上的方法。这种分解对于每个样本和每个特征（以及分类问题中的每个类别）都需要进行，因此生成了我们看到的数组结构。shap_values

三、实战

1、前提准备：数据预处理和划分数据集、基准随机森林模型rf_model

2、导包

import shap
import matplotlib.pyplot as plt

# 初始化 SHAP 解释器
explainer = shap.TreeExplainer(rf_model)
# 计算 SHAP 值（基于测试集），这个shap_values是一个numpy数组，表示每个特征对每个样本的贡献值
shap_values = explainer.shap_values(X_test)

1. shap_values(测试集特征) ✅

优势：解释模型在未见数据上的表现
注意：需确保explainer初始化时已包含训练集信息

2. shap_values(训练集特征) ❌

(需特殊处理)

使用训练集数据会暴露模型内部信息

3. shap_values(数据集全部特征) ❌

会导致数据泄露：

训练数据包含在解释数据中
破坏模型评估的客观性

1、SHAP 的维度要求

代码跑不通，甚至换个电脑就不行了等玄学问题，本质都是由于没有搞清楚shap的维度要求，这里记录下，希望对大家有所帮助。

分类问题和回归问题输出的shap_values的形状不同（重点）。

分类问题：shap_values.shap = (n_samples, n_features, n_classes)

回归问题：shap_values.shap = (n_samples, n_features)

数据维度的要求将是未来学习神经网络最重要的东西之一

搞懂了数据维度的要求，就可以知道如何去调整模型的输入数据，从而使得模型的输出数据符合shap_values的要求。

# 每一行代表一个样本，每一列代表一个特征，值表示该特征对该样本的预测结果的影响程度。
# 正值表示对该预测结果有正向影响，负值表示负向影响，某一样本的某一特征对标签0/1的影响程度是对称的。
shap_values

输出：

array([[[ 9.07465700e-03, -9.07465700e-03],
        [ 7.21456498e-03, -7.21456498e-03],
        [ 4.55189444e-02, -4.55189444e-02],
        ...,
        [ 7.12857198e-05, -7.12857198e-05],
        [ 4.67733508e-05, -4.67733508e-05],
        [ 1.61298135e-04, -1.61298135e-04]],

       [[-1.02606871e-02,  1.02606871e-02],
        [ 1.85572634e-02, -1.85572634e-02],
        [-1.64992848e-02,  1.64992848e-02],
        ...,
        [ 2.00070852e-04, -2.00070852e-04],
        [ 5.11798841e-05, -5.11798841e-05],
        [ 1.02827796e-04, -1.02827796e-04]],

       [[ 3.21529115e-03, -3.21529115e-03],
        [ 1.28184070e-02, -1.28184070e-02],
        [ 1.02124914e-01, -1.02124914e-01],
        ...,
        [ 1.73012306e-04, -1.73012306e-04],
        [ 4.74133256e-05, -4.74133256e-05],
        [ 1.26753231e-04, -1.26753231e-04]],

       ...,

       [[ 1.15222741e-03, -1.15222741e-03],
        [-1.71843266e-02,  1.71843266e-02],
        [-3.04994337e-02,  3.04994337e-02],
        ...,
        [ 1.44859329e-04, -1.44859329e-04],
        [ 1.80111014e-05, -1.80111014e-05],
        [ 1.30107512e-04, -1.30107512e-04]],

       [[ 1.29249120e-03, -1.29249120e-03],
        [ 5.66948438e-03, -5.66948438e-03],
        [ 2.49050264e-02, -2.49050264e-02],
        ...,
        [ 2.50590715e-06, -2.50590715e-06],
        [ 4.68839113e-05, -4.68839113e-05],
        [ 1.15002997e-05, -1.15002997e-05]],

       [[-1.12640555e-03,  1.12640555e-03],
        [ 1.42648293e-02, -1.42648293e-02],
        [ 4.74790019e-02, -4.74790019e-02],
        ...,
        [ 6.19451775e-05, -6.19451775e-05],
        [ 3.30996384e-05, -3.30996384e-05],
        [ 4.45219920e-05, -4.45219920e-05]]])

注：

整体是一个列表，里边有1500个列表，对应测试集中1500个样本，每一个长这样：

# 一个样本对应的列表
[[ 9.07465700e-03, -9.07465700e-03],
[ 7.21456498e-03, -7.21456498e-03],
[ 4.55189444e-02, -4.55189444e-02],
...,
[ 7.12857198e-05, -7.12857198e-05],
[ 4.67733508e-05, -4.67733508e-05],
[ 1.61298135e-04, -1.61298135e-04]]

其中又有31个列表，对应31个特征，每一个长这样：

[ 9.07465700e-03, -9.07465700e-03]

其中有两个值，分别表示对标签0和1的shap值。

2、查看形状并验证

shap_values.shape # 第一维是样本数，第二维是特征数，第三维是类别数

输出：

(1500, 31, 2)

# 验证维度
print(f"样本数: {shap_values.shape[0]}")  # 1500
print(f"特征数: {shap_values.shape[1]}")  # 31 
print(f"类别数: {shap_values.shape[2]}")  # 2（0=非违约，1=违约）

输出：

样本数: 1500
特征数: 31
类别数: 2

# 第1个样本中31个特征对预测结果的影响
shap_values[0]

输出：

array([[ 9.07465700e-03, -9.07465700e-03],
       [ 7.21456498e-03, -7.21456498e-03],
       [ 4.55189444e-02, -4.55189444e-02],
       [ 3.47666501e-04, -3.47666501e-04],
       [ 2.57821493e-04, -2.57821493e-04],
       [ 2.00758099e-03, -2.00758099e-03],
       [-7.54175659e-03,  7.54175659e-03],
       [-1.35324163e-03,  1.35324163e-03],
       [-7.08191659e-04,  7.08191659e-04],
       [-6.06829865e-03,  6.06829865e-03],
       [-1.90501403e-03,  1.90501403e-03],
       [ 1.44384291e-02, -1.44384291e-02],
       [-4.91452434e-02,  4.91452434e-02],
       [ 6.28172371e-03, -6.28172371e-03],
       [-1.64613559e-02,  1.64613559e-02],
       [-6.04576031e-01,  6.04576031e-01],
       [ 4.58074016e-04, -4.58074016e-04],
       [-1.95125086e-05,  1.95125086e-05],
       [-1.47478232e-05,  1.47478232e-05],
       [ 6.27274034e-04, -6.27274034e-04],
       [-1.26003035e-05,  1.26003035e-05],
       [-3.58303017e-04,  3.58303017e-04],
       [ 7.89740644e-05, -7.89740644e-05],
       [ 2.08492876e-04, -2.08492876e-04],
       [ 5.52330472e-06, -5.52330472e-06],
       [ 4.11019037e-04, -4.11019037e-04],
       [ 7.15614011e-06, -7.15614011e-06],
       [ 1.07037925e-04, -1.07037925e-04],
       [ 7.12857198e-05, -7.12857198e-05],
       [ 4.67733508e-05, -4.67733508e-05],
       [ 1.61298135e-04, -1.61298135e-04]])

数一数，确实有31个。

print("第1个样本的第2个特征对应的SHAP值为:",shap_values[0][1])

输出：

第1个样本的第2个特征对应的SHAP值为： [ 0.00721456 -0.00721456]

3、绘制SHAP图

寻找shap_values如何与X_test形状相同，不然后边没法做。

注：相同的操作，shap_values的形状可能会不同，我这里是（样本×特征×类别）上边已经展示了。你训练出来可能是（类别×样本×特征），很迷很抽象！！！

print("shap_values shape:", shap_values.shape)
print("shap_values[0] shape:", shap_values[0].shape)
print("shap_values[:, :, 0] shape:", shap_values[:, :, 0].shape)

print("X_test shape:", X_test.shape)

输出：

shap_values shape: (1500, 31, 2)
shap_values[0] shape: (31, 2)
shap_values[:, :, 0] shape: (1500, 31)
X_test shape: (1500, 31)

上面输出有点玄学，不用电脑可能输出不同，易得 shap_values[:, :, 0] 和 X_test 的尺寸一样，选它！

1.SHAP 特征重要性条形图

# --- 1. SHAP 特征重要性条形图 （Summary Plot - Bar） ---
print("--- 1. SHAP 特征重要性条形图 ---")
shap.summary_plot(shap_values[:, :, 0], X_test, plot_type="bar", show=False, max_display=10)
plt.title("SHAP Feature Importance (Bar Plot)")
plt.show()

--- 1. SHAP 特征重要性条形图 ---

当前模型重要程度前十的特征为：Credit Score、Current Loan Amount、Long Term、Annual Income、

Maximum Open Credit、Monthly Debt、Home Ownership、Current Credit Balance、

Years of Credit History、Number of Open Accounts

2.特征重要性蜂巢图

# --- 2.特征重要性蜂巢图(Summary Plot - Violin) ---
print("--- 2. SHAP 特征重要性蜂巢图 ---")
shap.summary_plot(shap_values[:, :, 0], X_test, plot_type="violin", show=False, max_display=10)  # 这里的show=False表示不直接显示图形,这样可以继续用plt来修改元素，不然就直接输出了
plt.title("SHAP Feature Importance (Bar Plot)")
plt.show()

--- 2. SHAP 特征重要性蜂巢图 ---

举例：Credit Score：越小（蓝色部分）越可能违约；越大（红色部分）违约可能性越小

3.SHAP 依赖性图

SHAP 依赖性图显示了单个特征在整个数据集中的影响。它们绘制了许多样本中特征的值与该特征的 SHAP 值的关系图，即揭示特征值与模型预测之间的关系，而非单纯的特征与特征的关系。
SHAP 依赖性图类似于部分依赖性图，但考虑了特征中存在的交互效应，并且仅在数据支持的输入空间区域中定义。

x轴为信用分数，点的颜色映射当前贷款金额值的分布，Y轴为对应样本的shap值。（图1）

# 揭示“Credit Score”和“Current Loan Amount”的联合影响模式
shap.dependence_plot('Current Credit Balance', shap_values[:, :, 0], X_test, interaction_index='Monthly Debt')

shap.dependence_plot('Annual Income', shap_values[:, :, 0], X_test, interaction_index='Monthly Debt')
shap.dependence_plot('Annual Income', shap_values[:, :, 0], X_test, interaction_index='Long Term')