教材170页第18题。删除数字求最小值
给定一个n位正整数a, 去掉其中k个数字后按原左右次序将组成一个新的正整数。对给定的a, k寻找一种方案,使得剩下的数字组成的新数最小。
提示:应用贪心算法设计求解
操作对象为n位正整数,有可能超过整数的范围,存储在数组a中,数组中每一个数组元素对应整数的一位数字。
在整数的位数固定的前提下,让高位的数字尽量小,整数的值就小。这就是所要选取的贪心策略。
每次删除一个数字,选择一个使剩下的数最小的数字作为删除对象。
当k=1时,对于n位数构成的数删除哪一位,使得剩下的数据最小。删除满足如下条件的a[i]:它是第一个a[i]>a[i+1]的数,如果不存在则删除a[n]。
当k>1(当然小于n),按上述操作一个一个删除。每删除一个数字后,后面的数字向前移位。删除一个达到最小后,再从头即从串首开始,删除第2个,依此分解为k次完成。
若删除不到k个后已无左边大于右边的降序或相等,则停止删除操作,打印剩下串的左边n−k个数字即可(相当于删除了若干个最右边的数字)。
具体代码:
#include<stdio.h>
#include<stdlib.h>
void minest(int *p,int n,int k)
{
int i,j,t,s=0;
int *a=new int[n-k];
for(i=0;i<n-k+1;i++)
a[i]=0;
int min;
if(n<k)
printf("这样子删除的结果无意义!\n");
else
{
for(i=0;i=n-k;i++)
{
min=p[s];
t=s;
for(j=s;j<=k+i;j++)
{
if(p[j]<min)
{
min=p[j];
t=j;
}
}
s=t+1;
a[i]=min;
}
for(i=0;i<n-k;i++)
printf("%d",a[i]);
}
}
void main()
{
int n,i,k;
printf("n位正整数的n值为: ");
scanf("%d",&n);
int *p=new int[n];
printf("这个正整数的值为:");
for(i=0;i<n;i++)
{
if(i==0)p[0]=rand()%8+1;
else p[i]=rand()%9;
printf("%d",p[i]);
}
printf("\n");
printf("需要删除的位数: ");
scanf("%d",&k);
minest(p,n,k);
delete []p;
}
结果截图:
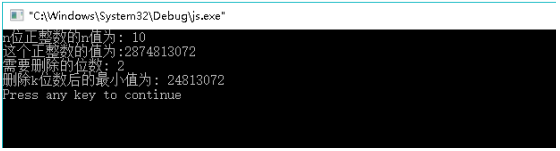




 本文介绍了一种使用贪心算法解决数学问题的方法,具体为从一个n位正整数中删除k个数字,使剩余数字组成的新数尽可能小。通过逐次选择删除能使剩余数字最小化的数字,实现算法目标。
本文介绍了一种使用贪心算法解决数学问题的方法,具体为从一个n位正整数中删除k个数字,使剩余数字组成的新数尽可能小。通过逐次选择删除能使剩余数字最小化的数字,实现算法目标。
















 2268
2268

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








