目录
一、前言
前面学过的数据结构,包括向量、链表、栈、队列,从物理上或者逻辑上来说,存在一定的前后次序,并且前驱和后继是唯一的,因此称之为线性结构。然而,向量的插入和删除操作、链表的循秩访问等操作,复杂度都非常高。树的结构,可以把两种结构的优势结合起来。
与前两种结构不同,树不存在天然的直接后继或者直接前驱关系,不过,我们可以通过定义一些约束,在树中确定节点之间的线性次序。树属于半线性结构。从结构来看,树其实是一种特殊的图,等价于连通无环图。与图一样,树也由一组顶点以及之间的联边组成,外加指定一个特定的根节点。
二、树的几个概念
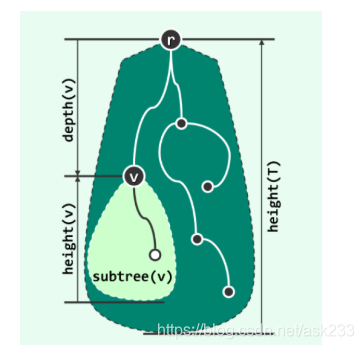
深度(depth):如图所示,根节点为r,v是一个树中间的节点。v的深度,即为v到r的唯一通路经过的边的个数,记作depth(v)。
祖先(ancestor)、后代(descendant):任一节点v在通往树根沿途所经过的每个节点都是其祖先,v是他们的后代。特别地,如果u恰好比v高一层,则u是v的父亲(parent),v是u的孩子(child)。
度数(degree):v孩子的个数,称为v的度数,记作deg(v)。
叶节点(leaf):如果节点v没有后代,那么v称为叶节点。
子树(subtree):v及其后代,以及他们直接的联边,称为一颗子树,记作subtree(v)。
高度(height):树T中所有节点深度的最大值,称作该树的高度,记作height(T),推广这一定义,节点v对应子树的高度,记作height(v)
三、二叉树
如果每个节点最多有两个孩子,即每个节点的度数均不超过2,称为二叉树(binary tree)。
性质

1.二叉树的遍历
以下遍历以该二叉树为例:
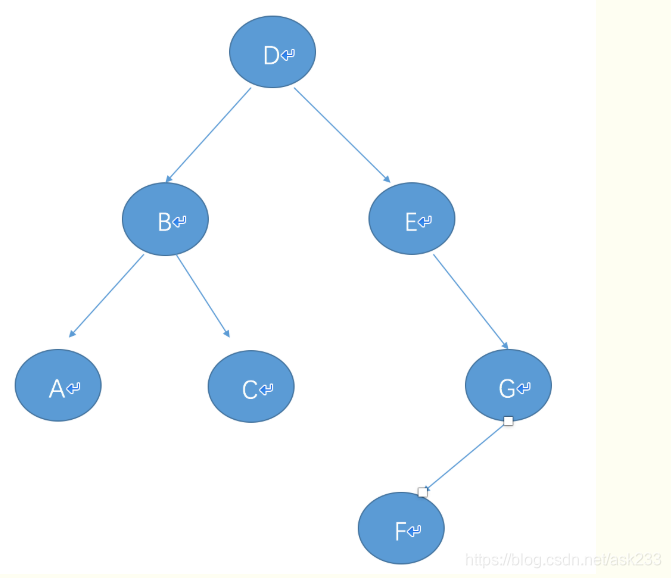
深度优先遍历
- 前序遍历
思想:先访问根节点,再先序遍历左子树,然后再先序遍历右子树。总的来说是根—左—右
- 中序遍历
思想:先中序访问左子树,然后访问根,最后中序访问右子树。总的来说是左—根—右
- 后序遍历
思想:先后序访问左子树,然后后序访问右子树,最后访问根。总的来说是左—右—根
递归实现:
void PreOrder(BiNode *bt)//前序遍历
{
if (bt != nullptr)
{
cout << bt->data << " ";
PreOrder(bt->lchild);
PreOrder(bt->rchild);
}
}
void InOrder(BiNode *bt)//中序遍历
{
if (bt == nullptr)
return;
else
{
InOrder(bt->lchild);
cout << bt->data << " ";
InOrder(bt->rchild);
}
}
void PostOrder(BiNode *bt)//后序遍历
{
if (bt == nullptr)
return;
else
{
PostOrder(bt->lchild);
PostOrder(bt->rchild);
cout << bt->data << " ";
}
}
非递归实现:
//前序遍历非递归实现
void preOrder(TreeNode *node) {
if (node == nullptr) {
return;
}
stack<TreeNode *> nstack;
nstack.push(node);
while (!nstack.empty()) {
TreeNode *temp = nstack.top();
cout << temp->val;
nstack.pop();
if (temp->right) {
nstack.push(temp->right);
}
if (temp->left) {
nstack.push(temp->left);
}
}
}
//中序遍历非递归实现
void inOrder(TreeNode *node) {
stack<TreeNode *> nstack;
TreeNode *temp = node;
while (temp || !nstack.empty())
{
if (temp) {
nstack.push(temp);
temp = temp->left;
}
else {
temp = nstack.top();
cout << temp->val;
nstack.pop();
temp = temp->right;
}
}
}
//后序遍历非递归实现
void posOrder(TreeNode *node) {
if (node == nullptr)
return;
stack<TreeNode *> nstack1, nstack2;
nstack1.push(node);
while (!nstack1.empty()) {
TreeNode *temp = nstack1.top();
nstack1.pop();
nstack2.push(temp);
if (temp->left)
nstack1.push(temp->left);
if (temp->right)
nstack1.push(temp->right);
}
while (!nstack2.empty())
{
cout << nstack2.top()->val;
nstack2.pop();
}
}层次遍历(宽度优先遍历)
思想:利用队列,依次将根,左子树,右子树存入队列,按照队列的先进先出规则来实现层次遍历。
//层序遍历二叉树:从上到下,从左到右
void Levelorder(TreeNode* t)
{
if (t == nullptr)
return;
deque<TreeNode*> dequeTreeNode;
dequeTreeNode.push_back(t);
while (!dequeTreeNode.empty())
{
//依次取出队列中的头部元素进行打印
TreeNode *pNode = dequeTreeNode.front();
cout << pNode->val << " ";
dequeTreeNode.pop_front(); //删除首部元素
if (pNode->left)
dequeTreeNode.push_back(pNode->left);
if (pNode->right)
dequeTreeNode.push_back(pNode->right);
}
}2.二叉树常见问题
2.1 重建二叉树
问题描述:
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
思路:
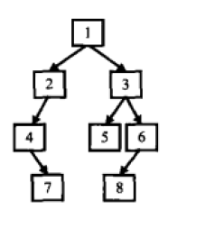
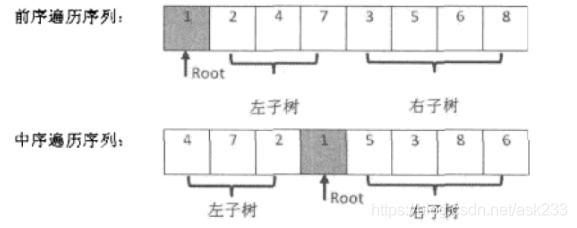
代码:
class Node:
def __init__(self,data):
self.data = data
self.left = None
self.right = None
'''
重建二叉树
'''
class Solution():
def reconstructBinaryTree(self,pre,tin):
# 返回构造树的根节点
if not pre and not tin:
return None
if set(pre) != set(tin):
return None
res = Node(pre[0])
res.left = self.reconstructBinaryTree(pre[1:tin.index(pre[0])+1],tin[:tin.index(pre[0])])
res.right = self.reconstructBinaryTree(pre[tin.index(pre[0])+1:],tin[tin.index(pre[0])+1:])
return res测试:
# 后序输出
if __name__ == '__main__':
s = Solution()
pre_order = [1, 2, 4, 7, 3, 5, 6, 8]
mid_order = [4, 7, 2, 1, 5, 3, 8, 6]
root = s.reconstructBinaryTree(pre_order, mid_order)
s.postorder(root)结果:
7 4 2 5 8 6 3 12.2 二叉树的下一个节点
题目描述:

思路:
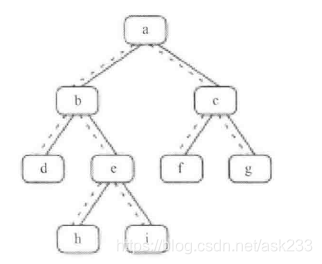
结合图,我们可发现分成两大类:
1、有右子树的,那么下个结点就是右子树最左边的点。(例如:b的下一个节点是h;a的下一个节点是f)
2、没有右子树的,也可以分成两类:
a)是父节点左孩子,那么父节点就是下一个节点 。(例如:d的下一个节点是b;f的下一个节点是c)
b)是父节点的右孩子,沿着父节点指针向上遍历,直到当前结点是其父节点的左孩子。如果没有父节点,它就是尾节点。例如:i的下一个节点是a;g没有下一个节点。
class Node:
def __init__(self,data):
self.data = data
self.left = None
self.right = None
# 指向父节点
self.next = None
class Solution():
def GetNext(self, pNode):
if not pNode:
return
#如果该节点有右子树,那么下一个节点就是它右子树中的最左节点
elif pNode.right!=None:
pNode=pNode.right
while pNode.left!=None:
pNode=pNode.left
return pNode
#如果一个节点没有右子树,并且它还是它父节点的右子节点
elif pNode.next!=None and pNode.next.right==pNode:
while pNode.next!=None and pNode.next.left!=pNode:
pNode=pNode.next
return pNode.next
#如果一个节点是它父节点的左子节点,那么直接返回它的父节点
else:
return pNode.next2.3 树的子结构
题目描述:
输入两棵二叉树A,B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
思路:
- 在树A中找到和树B的根节点的值一样的节点R
- 判断树A中以R为根节点的子树是不是包含和树B一样的结构
class Node():
def __init__(self,data,left = None,right = None):
self.data = data
self.left = left
self.right = right
class Solution():
def hasSubTree(self,root1,root2):
result = False
if root1 != None and root2 != None:
if root1.data == root2.data:
result = self.doesTree1HaveTree2(root1,root2)
# 判断左子树中是否包含B树结构
if not result:
result = self.hasSubTree(root1.left,root2)
# 判断右子树中是否包含B树结构
if not result:
result = self.hasSubTree(root1.right,root2)
return result
def doesTree1HaveTree2(self,root1,root2):
# 若B树为空,那么B是A的子结构
if not root2:
return True
if not root1:
return False
if root1.data != root2.data:
return False
return self.doesTree1HaveTree2(root1.left,root2.left) and \
self.doesTree1HaveTree2(root1.right,root2.right) 测试:
if __name__ == "__main__":
tree1_7 = Node(data=7)
tree1_6 = Node(data=4)
tree1_5 = Node(data=2, left=tree1_6, right=tree1_7)
tree1_4 = Node(data=9)
tree1_3 = Node(data=7)
tree1_2 = Node(data=8, left=tree1_4, right=tree1_5)
tree1_1 = Node(data=8, left=tree1_2, right=tree1_3)
tree1 = tree1_1
tree2_3 = Node(2)
tree2_2 = Node(9)
tree2_1 = Node(8, left=tree2_2, right=tree2_3)
tree2 = tree2_1
s =Solution()
print(s.hasSubTree(tree1, tree2))结果:
True2.4 二叉树中和为某一值的路径
题目描述:
输入一颗二叉树和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
思路:
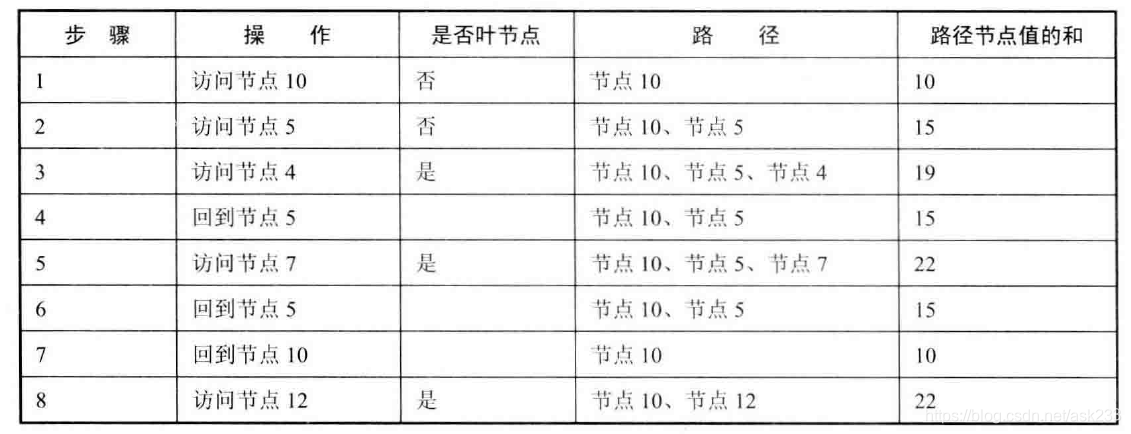
当用前序遍历的方式访问到某一节点时,我们把该节点添加到路径上,并累加该节点的值。如果该节点为叶节点,并且路径中节点值的和刚刚好等于输入的整数,则当前路径符合要求,然后打印该路径。如果当前节点不是叶节点,那么继续访问它的子节点。当前节点访问结束之后,递归函数将自动回到它的父节点。因此,我们在函数退出之前需要在路径上删除当前节点并减去当前节点的值,以确保返回父节点时路径刚好是从根节点到父节点。
根据上述分析,可以得出储存容器需要用到数据结构的栈,对于递归的调用就是一个压栈和出栈的过程。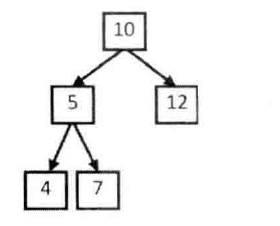
代码:
class BinaryTreeNode():
def __init__(self,data,left=None,right=None):
self.data = data
self.left = left
self.right = right
class Solution():
def findPath(self,root,expectedSum):
if root == None:
return
path = []
currentSum = 0
self.pathSum(root,expectedSum,path,currentSum)
def pathSum(self,root,expectedSum,path,currentSum):
currentSum += root.data
path.append(root.data)
if not root.left and not root.right and currentSum == expectedSum:
print('A Path is Found:')
print(' '.join([str(n) for n in path]))
# 如果不是叶节点,则遍历它的子节点
if root.left != None:
self.pathSum(root.left,expectedSum,path,currentSum)
if root.right != None:
self.pathSum(root.right,expectedSum,path,currentSum)
path.pop()测试:
if __name__ == "__main__":
node5 = BinaryTreeNode(7)
node4 = BinaryTreeNode(4)
node3 = BinaryTreeNode(12)
node2 = BinaryTreeNode(5, node4, node5)
node1 = BinaryTreeNode(10, node2, node3)
root = node1
s = Solution()
s.findPath(root, 22)结果:
A Path is Found:
10 5 7
A Path is Found:
10 122.5 二叉树的深度
题目描述:

思路:
在2.4“二叉树中和为某一值的路径”中讨论了如何记录树的路径,这种思路代码量较大,可以尝试简洁的方法。
①如果一棵树只有一个结点,它的深度为1。
②如果根结点只有左子树而没有右子树,那么树的深度应该是其左子树的深度加1;同样如果根结点只有右子树而没有左子树,那么树的深度应该是其右子树的深度加1。
③如果既有右子树又有左子树,那该树的深度就是其左、右子树深度的较大值再加1。

代码:
class BinaryTreeNode():
def __init__(self,data,left = None,right = None):
self.data = data
self.left = left
self.right = right
class Solution():
'''
递归解法, 简单直接, 时间复杂度O(n), 空间复杂度O(logn)
'''
def treeDepth(self,root):
if root == None:
return 0
else:
return max(self.treeDepth(root.left),self.treeDepth(root.right)) + 1
# 非递归算法,利用一个栈以及一个标志位栈
def TreeDepth2(self, pRoot):
if not pRoot:
return 0
depth = 0
stack, tag = [], []
pNode = pRoot
while pNode or stack:
while pNode:
stack.append(pNode)
tag.append(0)
pNode = pNode.left
if tag[-1] == 1:
depth = max(depth, len(stack))
stack.pop()
tag.pop()
pNode = None
else:
pNode = stack[-1]
pNode = pNode.right
tag.pop()
tag.append(1)
return depth测试:
if __name__ == "__main__":
node5 = BinaryTreeNode(7)
node4 = BinaryTreeNode(4)
node3 = BinaryTreeNode(12)
node2 = BinaryTreeNode(5, node4, node5)
node1 = BinaryTreeNode(10, node2, node3)
root = node1
s = Solution()
print(s.treeDepth(root))结果:
32.6 二叉树的镜像
题目描述:
操作给定的二叉树,将其变换为源二叉树的镜像。
二叉树的镜像定义:
源二叉树 镜像二叉树
8 8
/ \ / \
6 10 10 6
/ \ / \ / \ / \
5 7 9 11 11 9 7 5
思路:
- 递归:

上图求二叉树镜像的过程
(a)交换根节点的左、右子树;
(b)交换值为10的节点的左、右子节点;
(c)交换值为6的节点的左、右子节点。
总结上面的过程,我们得出求一棵树的镜像的过程:先序遍历这棵树的每个节点,如果遍历到的节点有子节点,就交换它的两个子节点。当交换完所有的非叶节点的左、右子节点之后,就得到了树的镜像。
class TreeNode:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
class Solution():
'''
递归实现,时间复杂度为O(n)。
'''
def mirrorRecursively(self,root):
if root == None:
return None
if not root.left and not root.right:
return root
root.left , root.right = root.right , root.left
if root.left:
self.mirrorRecursively(root.left)
if root.right:
self.mirrorRecursively(root.right)- 非递归:
思路1:层次遍历,根节点不为 null 将根节点入队,判断队不为空时,节点出队,交换该节点的左右孩子,如果左右孩子不为空,将左右孩子入队。
class TreeNode:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
class Solution():
# 非递归实现
def MirrorNoRecursion(self, root):
if root == None:
return
nodeQue = [root]
while len(nodeQue) > 0:
curLevel, count = len(nodeQue), 0
while count < curLevel:
count += 1
pRoot = nodeQue.pop(0)
pRoot.left, pRoot.right = pRoot.right, pRoot.left
if pRoot.left:
nodeQue.append(pRoot.left)
if pRoot.right:
nodeQue.append(pRoot.right)思路2:
先序遍历,如果根节点不为 null 将根节点入栈,当栈不为 null 出栈,交换左右节点,如果左右节点不为 null 入栈。
class TreeNode:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
class Solution():
# 非递归实现
def Mirror2(self, root):
if root == None:
return
stackNode = []
stackNode.append(root)
while len(stackNode) > 0:
nodeNum = len(stackNode) - 1
tree = stackNode[nodeNum]
stackNode.pop()
nodeNum -= 1
if tree.left != None or tree.right != None:
tree.left, tree.right = tree.right, tree.left
if tree.left:
stackNode.append(tree.left)
nodeNum += 1
if tree.right:
stackNode.append(tree.right)
nodeNum += 1
测试:
if __name__ == "__main__":
pNode1 = TreeNode(8)
pNode2 = TreeNode(6)
pNode3 = TreeNode(10)
pNode4 = TreeNode(5)
pNode5 = TreeNode(7)
pNode6 = TreeNode(9)
pNode7 = TreeNode(11)
pNode1.left = pNode2
pNode1.right = pNode3
pNode2.left = pNode4
pNode2.right = pNode5
pNode3.left = pNode6
pNode3.right = pNode7
S = Solution()
S.Mirror2(pNode1)
#S.mirrorRecursively(pNode1)
print(pNode1.right.left.data)结果:
72.7 对称的二叉树
题目描述:
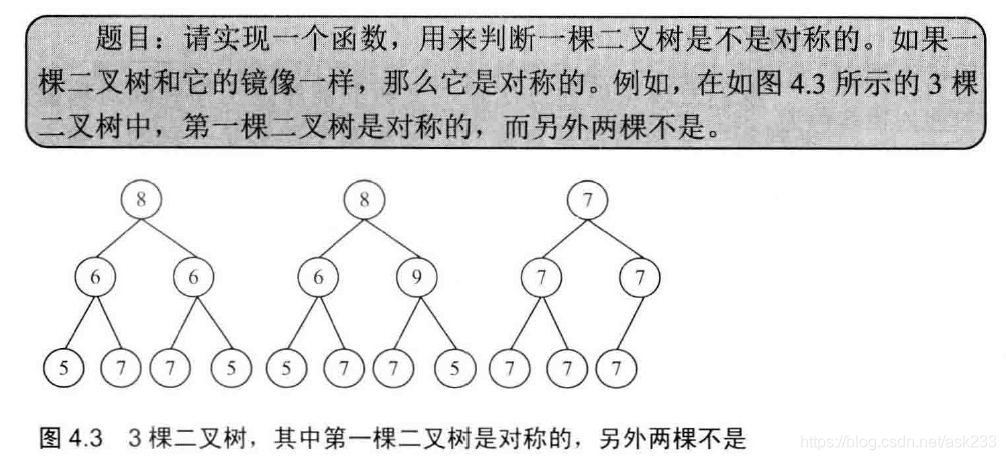
思路:
对于一棵二叉树,从根结点开始遍历:
- 如果左右子结点有一个为NULL,那么肯定不是对称二叉树;
- 如果左右子结点均不为空,但不相等,那么肯定不是对称二叉树;
- 如果左右子结点均不为空且相等,那么
- 遍历左子树,遍历顺序为:当前结点,左子树,右子树;
- 遍历右子树,遍历顺序为:当前结点,右子树,左子树;
- 如果遍历左子树的序列和遍历右子树的序列一样,那么该二叉树为对称的二叉树。(递归实现)

代码:
class TreeNode:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
class Solution():
'''
递归
左子树按照中左右的顺序遍历,
右子树按照中右左的顺序遍历,如果每一步访问的值都相同,说明左右子树对称
'''
def isSymmetrical(self,root1,root2):
if not root1 and not root2:
return True
if not root1 or not root2:
return False
if root1.data != root2.data:
return False
return self.isSymmetrical(root1.left,root2.right) \
and self.isSymmetrical(root1.right,root2.left)
def SymmetricalTree(self,root):
return self.isSymmetrical(root.left,root.right)
'''
非递归
使用栈(或者队列),把需要比较的两个节点压进栈,再依次比较。
'''
def isSymmetrical2(self, root):
if not root:
return True
nodeList = [root.left,root.right]
while nodeList:
symmetricLeft = nodeList.pop(0)
symmetricRight = nodeList.pop(0)
if not symmetricLeft and not symmetricRight:
continue
if not symmetricLeft or not symmetricRight:
return False
if symmetricLeft.data != symmetricRight.data:
return False
nodeList.append(symmetricLeft.left)
nodeList.append(symmetricRight.right)
nodeList.append(symmetricLeft.right)
nodeList.append(symmetricRight.left)
return True测试:
if __name__ == "__main__":
pNode1 = TreeNode(8)
pNode2 = TreeNode(6)
pNode3 = TreeNode(6)
pNode4 = TreeNode(5)
pNode5 = TreeNode(7)
pNode6 = TreeNode(7)
pNode7 = TreeNode(5)
pNode1.left = pNode2
pNode1.right = pNode3
pNode2.left = pNode4
pNode2.right = pNode5
pNode3.left = pNode6
pNode3.right = pNode7
S = Solution()
print(S.SymmetricalTree(pNode1))
print(S.isSymmetrical2(pNode1))结果:
True
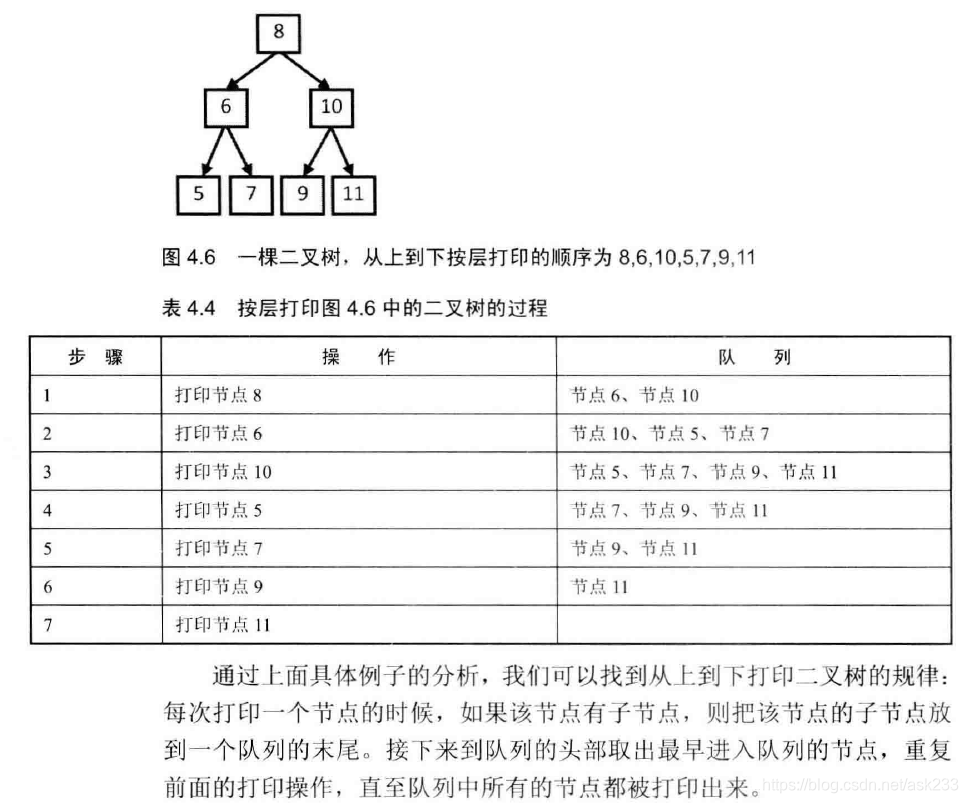
True2.8 从上到下打印二叉树
题目描述:

思路:
代码:
class Node:
def __init__(self,data,left=None,right=None):
self.data = data
self.left = left
self.right = right
class Solution():
def printFromTopToBottom(self,root):
if root == None:
return
queue = []
queue.append(root)
while queue:
cur = queue.pop(0)
print(cur.data,end=' ')
if cur.left:
queue.append(cur.left)
if cur.right:
queue.append(cur.right)测试:
if __name__ == "__main__":
pNode1 = TreeNode(8)
pNode2 = TreeNode(6)
pNode3 = TreeNode(10)
pNode4 = TreeNode(5)
pNode5 = TreeNode(7)
pNode6 = TreeNode(9)
pNode7 = TreeNode(11)
pNode1.left = pNode2
pNode1.right = pNode3
pNode2.left = pNode4
pNode2.right = pNode5
pNode3.left = pNode6
pNode3.right = pNode7
S = Solution()
S.printFromTopToBottom(pNode1)结果:
8 6 10 5 7 9 11题目描述:
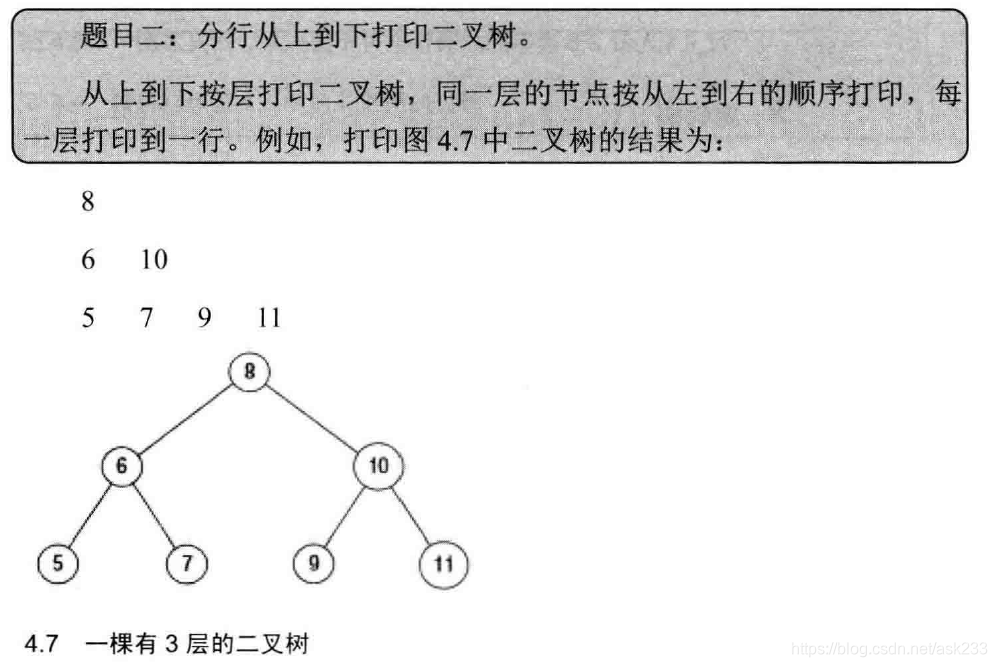
思路:
用一个队列保存将要打印的节点,为了把二叉树的每一行单独打印到一行里,需要两个变量:一个变量表示当前层中还没有打印的节点数;另一个变量表示下一层节点的数目。
代码:
class TreeNode:
def __init__(self,data):
self.data = data
self.left = None
self.right = None
class Solution():
'''
分行从上到下打印二叉树
'''
def branchPrint(self,root):
if root == None:
return
queue = []
queue.append(root)
# 下一层的节点数
nextLevel = 0
# 当前还没有打印的节点数
toBePrinted = 1
while queue:
cur = queue.pop(0)
print(cur.data,end = ' ')
if cur.left:
queue.append(cur.left)
nextLevel += 1
if cur.right:
queue.append(cur.right)
nextLevel += 1
toBePrinted -= 1
if toBePrinted == 0:
print()
toBePrinted = nextLevel
nextLevel = 0测试:
if __name__ == "__main__":
pNode1 = TreeNode(8)
pNode2 = TreeNode(6)
pNode3 = TreeNode(10)
pNode4 = TreeNode(5)
pNode5 = TreeNode(7)
pNode6 = TreeNode(9)
pNode7 = TreeNode(11)
pNode1.left = pNode2
pNode1.right = pNode3
pNode2.left = pNode4
pNode2.right = pNode5
pNode3.left = pNode6
pNode3.right = pNode7结果:
8
6 10
5 7 9 11题目描述:

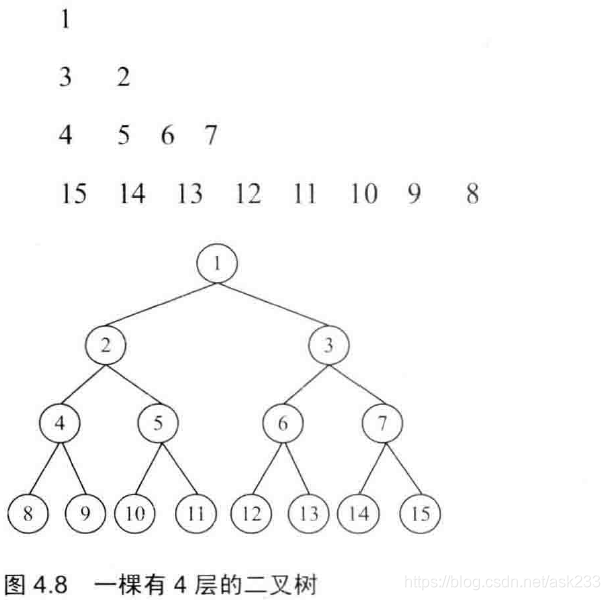
思路:

代码:
class TreeNode:
def __init__(self,data):
self.data = data
self.left = None
self.right = None
class Solution():
'''
按之字形顺序打印二叉树
'''
def ZPrint(self, pRoot):
resultArray = []
if not pRoot:
return resultArray
curLayerNodes = [pRoot]
isEvenLayer = True
while curLayerNodes:
curLayerValues = []
nextLayerNodes = []
isEvenLayer = not isEvenLayer
for node in curLayerNodes:
curLayerValues.append(node.data)
if node.left:
nextLayerNodes.append(node.left)
if node.right:
nextLayerNodes.append(node.right)
curLayerNodes = nextLayerNodes
if isEvenLayer:
curLayerValues.reverse()
print(curLayerValues)2.9 序列化二叉树
题目描述:
请实现两个函数,分别用来序列化和反序列化二叉树。
思路:
序列化二叉树:把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串。需要注意的是,序列化二叉树的过程中,如果遇到空节点,需要以某种符号(这里用#)表示。以下图二叉树为例,序列化二叉树时,需要将空节点也存入字符串中。
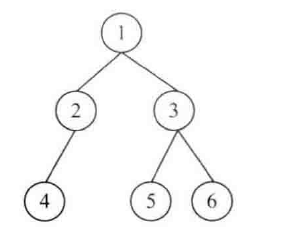
序列化可以基于先序/中序/后序/按层等遍历方式进行,这里采用先序遍历的方式实现,字符串之间用 “,”隔开。
代码:
class BinaryTree:
def __init__(self,data):
self.data = data
self.left = None
self.right = None
class Solution():
def serialize(self,root):
if root == None:
return '#'
return str(root.data) + ',' + self.serialize(root.left) \
+ ',' + self.serialize(root.right)
def Deserialize(self, s):
lst = s.split(',')
return self.deserializeTree(lst)
def deserializeTree(self, lst):
if len(lst) <= 0:
return None
val = lst.pop(0)
root = None
if val != '#':
root = BinaryTree(int(val))
root.left = self.deserializeTree(lst)
root.right = self.deserializeTree(lst)
return root
# 前序遍历
def preorder(self,root):
if root == None:
return
print(root.data,end=' ')
self.preorder(root.left)
self.preorder(root.right)测试:
if __name__ == "__main__":
pNode1 = BinaryTree(1)
pNode2 = BinaryTree(2)
pNode3 = BinaryTree(3)
pNode4 = BinaryTree(4)
pNode5 = BinaryTree(5)
pNode6 = BinaryTree(6)
pNode1.left = pNode2
pNode1.right = pNode3
pNode2.left = pNode4
pNode3.left = pNode5
pNode3.right = pNode6
S = Solution()
serializeRes = S.serialize(pNode1)
print('序列化二叉树:', serializeRes)
deserializeRes = S.Deserialize(serializeRes)
print('反序列化二叉树:', end=' ')
S.preorder(deserializeRes)结果:
序列化二叉树: 1,2,4,#,#,#,3,5,#,#,6,#,#
反序列化二叉树: 1 2 4 3 5 6四、二叉树特例—二叉搜索树
1. 基本概念
叉搜索树(Binary Search Tree),又名二叉排序树(Binary Sort Tree),是以一棵二叉树来组织的,可以用链表数据结构来表示,其中,每一个结点就是一个对象,一般地,包含数据内容key和指向孩子(也可能是父母)的指针属性。如果某个孩子结点不存在,其指针属性值为空(NIL)。
二叉搜索树中的关键字key的存储方式总是满足二叉搜索树的性质:
设x是二叉搜索树中的一个结点。如果y是x左子树中的一个结点,那么会有y.key<=x.key;如果y是x右子树中的一个节点,那么有y.key>=x.key。
2. 二叉搜索树相关操作
搜索树数据结构支持许多动态集合操作,包括SEARCH(查找指定结点)、MINIMUM(最小关键字结点)、MAXMUM(最大关键字结点)、PREDECESSOR(结点的先驱)、SUCCESSOR(结点的后继)、INSERT(结点的插入)和DELETE(结点的删除)等。因此,我们使用一棵搜索树既可以作为一个字典又可以作为一个优先队列。
2.1 查找
二叉搜索树很多时候用来进行数据查找。这个过程从树的根结点开始,沿着一条简单路径一直向下,直到找到数据或者得到NIL值。
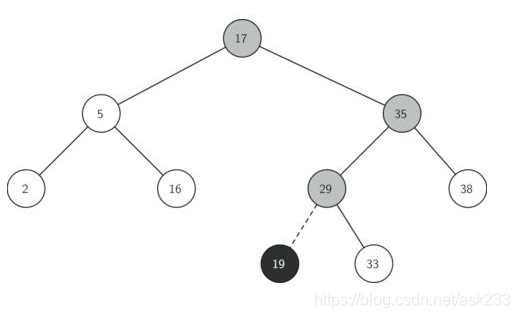
由图可以看出,对于遇到的每个结点x,都会比较x.key与k的大小,如果相等,就终止查找,否则,决定是继续往左子树还是右子树查找。因此,整个查找过程就是从根节点开始一直向下的一条路径,若树的高度是h,那么查找过程的时间复杂度就是O(h)。
BST查找的递归算法与非递归算法伪代码分别如下:
//递归实现
Tree_Search(x, k):
if x == NIL or x.key == k :
return x
if k < x.key
return Tree_Search(x.left, k)
else return Tree_Search(x.right, k)//非递归迭代实现
Tree_Search(x, k) :
while x!=NIL and k!=x.key:
if k < x.key
x = x.left
else x = x.right
return x2.2 最大关键字元素和最小关键字元素
通过从树根开始沿着left leftleft孩子指针直到遇到一个null nullnull,我们总能在一颗二叉搜索树中找到一个元素,如下所示。
Tree_minimum(x):
while x.left != NIL
x = x.left
return xTree_maxnum(x):
while x.right != NIL
x = x.right
return x寻求最大关键字元素的过程MAXMUM是对称的。这两个过程在一棵高度为h的树中均能在O(h)时间内执行完毕。
2.3 后继与前驱
对于给定的一棵二叉搜索树中的节点,按照中序遍历的次序,如果所有结点的key均不相同
定义:一个结点的后继,是大于x.key的最小关键字的结点。
一个结点的前驱,是小于x.key的最大关键字的结点。
思路:找一个结点的前驱或者后继,无非是在三个区域找。
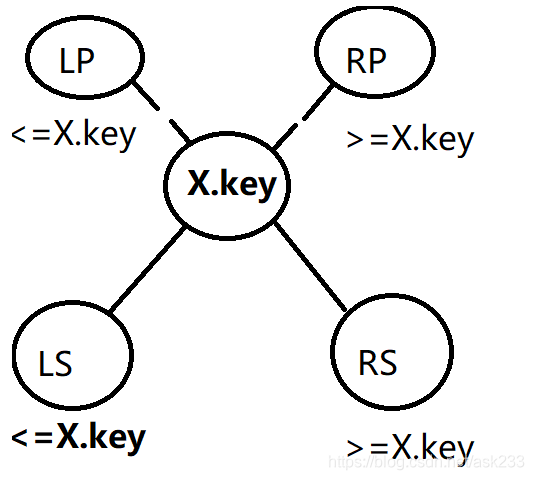
首先分析前驱:
满足两个条件,一是要小于当前键值,那么只有LP和LS区可以找。 二要求是其中最大的值。我们知道,对于LP来说,X、LS、RS都属于他的右子树,那么,X、LS和RS都是大于它的。
所以很显然,前驱就是LS中的最大值,即前驱 = 左子树中的最大值。条件是:存在左子树。
那不存在左子树只有左父母的情况呢?
那只能在LP上找了,LP也具有两部分,第一部分是LP的LS,LP的LS虽然满足小于X的条件,但是LP的LS中所有元素都是小于LP的,所以至少也是LP。
还有一部分,LP可能有左父母或者右父母,显然,右父母大于他的所有左子树,包括X,条件一都不满足,显然不行。左父母小于LP,所以它竞争不过LP。
所以最终结论就是,在只有左父母,没有左子树的情况,前驱 = 左父母的值。
那不存在左子树和左父母的情况呢?
那就只剩下右子树和右父母了,显然,右子树肯定不行,它的所有元素都大于X。那就只能在右父母中找了,毕竟虽然右父母大于它,但是右父母也有左/右父母和右子树。
右父母的右父母,和右子树都不行,都大于右父母本身,更大于X了。那就只能在右父母的左父母上找了,对于左父母来说,他的右子树全都大于他,即包括X的右父母和X,所以,此时找到的左父母就是我们的前驱。
所以,不存在左子树和左父母的情况,前驱 = 右父母的左父母(如果右父母不存在左父母,就一直往上遍历,直至出现左父母)。
分析完毕。下面是伪代码实现。
TREE-predecessor(x)
if x.left ≠ NIL
return TREE-MAXIMUM(x.left)
y = x.p
while y ≠ NIL and x == y.left
x = y
y = y.p
return y接着分析后继:(类比前驱,如果前驱看懂了可以不用看,基本上是一样的分析思路)
满足两个条件,一是要大于当前键值,那么只有RP和RS区可以找。 二要求是其中最小的值。我们知道,对于RP来说,X、LS、RS都属于他的左子树,那么,X、LS和RS都是小于它的。
所以很显然,前驱就是RS中的最小值,即后继 = 右子树中的最小值。条件是:存在右子树。
那不存在右子树只有右父母的情况呢?
那只能在RP上找了,RP也具有两部分,第一部分是RP的RS,RP的RS虽然满足大于X的条件,但是RP的RS中所有元素都是大于LP的,所以找后继,至少也得是RP。
还有一部分,RP可能有左父母或者右父母,显然,左父母小于他的所有右子树,包括X,条件一都不满足,显然不行。右父母大于RP,所以它竞争不过RP。
所以最终结论就是,在只有右父母,没有右子树的情况,后继 = 右父母的值。
那不存在右子树和右父母的情况呢?
那就只剩下左子树和左父母了,显然,左子树肯定不行,它的所有元素都小于X。那就只能在左父母中找了,毕竟虽然左父母小于它,但是右父母也有它本身的左/右父母和左子树。
左父母的左父母,和左子树都不行,都小于左父母本身,更小于X了。那就只能在左父母的右父母上找了,对于它的右父母来说,他的左子树全都小于他,即包括X的左父母和X,所以,此时找到的右父母就是我们的后继。
所以,不存在右子树和右父母的情况,后继 = 左父母的右父母(如果左父母不存在右父母,就一直往上遍历,直至出现右父母)
后继结点的伪代码:
Tree_Successor(x):
if x.right != NIL
return Tree_Minimum(x.right)
y = x.p
while y!=NIL and x == y.right
x = y
y = y.p
return y假设树的高度是h,那么PREDECESSOR与SUCCESSOR过程的时间复杂度就是O(h)。
2.4 插入
BST的插入过程非常简单,很类似与二叉树搜索树的查找过程。当需要插入一个新结点时,从根节点开始,迭代或者递归向下移动,直到遇到一个空的指针NIL,需要插入的值即被存储在该结点位置。这里给出迭代插入算法,递归方式的比较简单。
伪码如下:
Tree_Insert(T, z):
y = NIL
x = T.root
while x != NIL
y = x
if z.key < x.key
x = x.left
else x = x.right
z.p = y
if y == NIL
T.root = z
else if z.key < y.key
y.left = z
else y.right = z二叉搜索树(BST)的插入操作的时间复杂度为O(h)。
python代码:
class BinarySearchTree:
def __init__(self,data):
self.data = data
self.left = None
self.right = None
class Solution():
'''
二叉搜索树插入操作
'''
# 递归实现
def insert(self, root, val):
if root == None:
root = BinarySearchTree(val)
elif val < root.data:
root.left = self.insert(root.left, val)
elif val > root.data:
root.right = self.insert(root.right, val)
return root
2.5 删除
二叉搜索树的结点删除比插入较为复杂,总体来说,结点的删除可归结为三种情况:
- 如果结点z没有孩子节点,那么只需简单地将其删除,并修改父节点,用NIL来替换z;
- 如果结点z只有一个孩子,那么将这个孩子节点提升到z的位置,并修改z的父节点,用z的孩子替换z;
- 如果结点z有两个孩子,那么查找z的后继y,此外后继一定在z的右子树中,然后让y替换z。
这三种情况中,1和2比较简单,3相对棘手。
情况1:

情况2:

情况3:
可分为两种类型,一种是z的后继y位于其右子树中,但没有左孩子,也就是说,右孩子y是其后继。如下:

另外一种类型是,z的后继y位于z的右子树中,但并不是z的右孩子,此时,用y的右孩子替换y,然后再用y替换z。如下:

为了完成二叉搜索树中结点的DELETE过程,我们需要定义一个子过程TRANSPLANT,它是用另一棵子树来替换一棵子树并成为其双亲的孩子结点。我们通过此过程来完成上述三种情况中的替换工作。TRANSPLANT过程如下。

通过子过程TRANSPLANT,便可以实现DELETE过程。

在一棵高度为h的二叉搜索树中,DELETE过程的运行时间为O(h)。
3. 二叉搜索树常见问题
3.1 二叉搜索树的后序遍历序列
问题描述:
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
思路:
首先要清楚,这道题不是让你去判断一个给定的数组是不是一个(原先)给定的二叉搜索树的对应后序遍历的结果,而是判断一个给定的数组是不是能够对应到一个具体的二叉搜索树的后序遍历结果,所以还是用递归的思想。
把数组分成三部分,比如[4,8,6,12,16,14,10],10就是根节点,4,8,6都是左子树,12,16,14都是右子树,然后针对左右子树再去判断是不是符合根节点、左右子树这一个规律(左子树都比根节点小,右子树都比根节点大)
代码:
class BinarySearchTree:
def __init__(self,data):
self.data = data
self.left = None
self.right = None
class Solution():
def verifySeqOfBST(self,sequence):
if len(sequence) == 0:
return False
root = sequence[-1]
index = 0
# 在二叉搜索树中左子树节点的值小于根节点的值
for i in range(len(sequence)):
if sequence[i] > root:
index = i
break
# 在二叉搜索树中左子树节点的值小于根节点的值
for j in range(i,len(sequence)):
if sequence[j] < root:
return False
# 判断左子树是不是二叉搜索树
left = True
if index > 0:
left = self.verifySeqOfBST(sequence[:index])
# 判断右子树是不是二叉搜索树
right = True
if index < len(sequence) - 1:
right = self.verifySeqOfBST(sequence[index+1:])
return left and right测试:
if __name__ == "__main__":
s = Solution()
seq1 = [5,7,9,11,10,8]
seq2 = [7,4,6,5]
print(s.verifySeqOfBST(seq1))
print(s.verifySeqOfBST(seq2))结果:
True
False3.2 二叉搜索树与双向链表
题目描述:
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。如图:
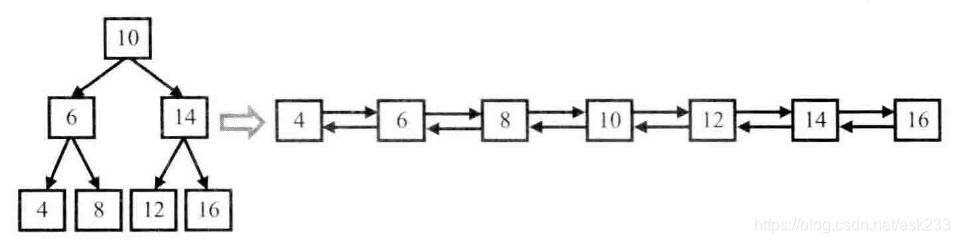
思路:
1:由于要求链表是有序的,可以借助二叉树中序遍历,因为中序遍历算法的特点就是从小到大访问结点。当遍历访问到根结点时,假设根结点的左侧已经处理好,只需将根结点与上次访问的最近结点(左子树中最大值结点)的指针连接好即可。进而更新当前链表的最后一个结点指针。
2:由于中序遍历过程正好是转换成链表的过程,即可采用递归处理
3:定义两个辅助节点listHead(链表头节点)、listTail(链表尾节点)。listHead用于记录链表的头节点,用于最后算法的返回;listTail用于定位当前需要更改指向的节点。
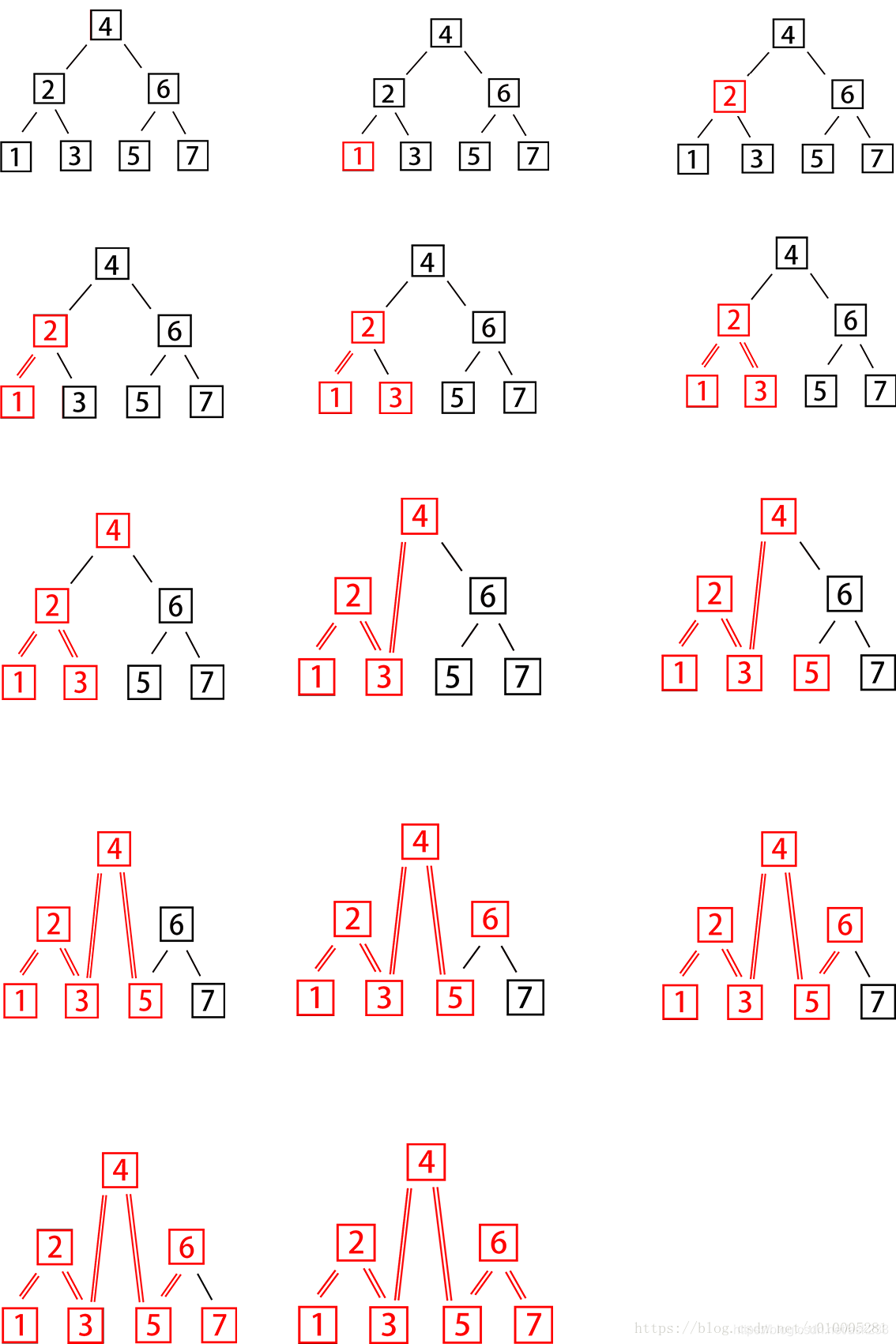
代码:
class BinarySearchTree:
def __init__(self,data):
self.data = data
self.left = None
self.right = None
class Solution:
def __init__(self):
self.listHead = None
self.listTail = None
def Convert(self, pRootOfTree):
if pRootOfTree == None:
return
self.Convert(pRootOfTree.left)
if self.listHead == None:
self.listHead = pRootOfTree
self.listTail = pRootOfTree
# 更改节点指向
else:
self.listTail.right = pRootOfTree
pRootOfTree.left = self.listTail
self.listTail = pRootOfTree
self.Convert(pRootOfTree.right)
return self.listHead
# 链表的正序和反序
def printList(self, head):
while head.right:
print(head.data, end=" ")
head = head.right
print(head.data)
while head:
print(head.data, end= " ")
head = head.left测试:
if __name__ == "__main__":
pNode1 = BinarySearchTree(10)
pNode2 = BinarySearchTree(6)
pNode3 = BinarySearchTree(14)
pNode4 = BinarySearchTree(4)
pNode5 = BinarySearchTree(8)
pNode6 = BinarySearchTree(12)
pNode7 = BinarySearchTree(16)
pNode1.left = pNode2
pNode1.right = pNode3
pNode2.left = pNode4
pNode2.right = pNode5
pNode3.left = pNode6
pNode3.right = pNode7
s = Solution()
head = s.Convert(pNode1)
s.printList(head)结果:
4 6 8 10 12 14 16
16 14 12 10 8 6 43.3 二叉搜索树的第K大节点
题目描述:

思路:
先对二叉搜索树进行中序遍历,在返回的列表中找到第k个节
代码:
class BinarySearchTree:
def __init__(self,data):
self.data = data
self.left = None
self.right = None
class Solution:
# 返回对应节点TreeNode
def __init__(self):
self.res = []
def KthNode(self, pRoot, k):
if k <= 0:
return None
self.inOrder(pRoot)
if len(self.res) < k:
return None
return self.res[k - 1]
def inOrder(self, root):
if not root:
return
if root.left:
self.inOrder(root.left)
self.res.append(root)
if root.right:
self.inOrder(root.right)测试:
if __name__ == "__main__":
pNode1 = BinarySearchTree(5)
pNode2 = BinarySearchTree(3)
pNode3 = BinarySearchTree(7)
pNode4 = BinarySearchTree(2)
pNode5 = BinarySearchTree(4)
pNode6 = BinarySearchTree(6)
pNode7 = BinarySearchTree(8)
pNode1.left = pNode2
pNode1.right = pNode3
pNode2.left = pNode4
pNode2.right = pNode5
pNode3.left = pNode6
pNode3.right = pNode7
s = Solution()
res = s.KthNode(pNode1,3)
print(res.data)结果:
43.4 二叉树中两个节点的最低公共祖先
情形1、二叉搜索树
分析:如果树是二叉搜索树的话,就比较容易解决。因为二叉搜索树的特性,左子树的上节点的值比根节点小,右子树上节点的值比根节点大。
思路:从树的根节点开始和两个输入的节点进行比较。
(1)如果当前节点的值比两个节点的值都大,最低公共祖先结点一定在当前结点的左子树。
(2)如果当前节点的值比两个节点的值都小,最低公共祖先节点一定在当前结点的右子树。
(3)如果一个结点比当前结点大或等于,另一个比当前结点小或等于,则最低公共祖先节点为当前结点。
时间复杂度为O(lgN),空间复杂度为O(1)。
class BinarySearchTree:
def __init__(self,data):
self.data = data
self.left = None
self.right = None
class Solution():
'''
树是二叉树,且是二叉搜索树
'''
def getLastCommomParent(self,pRoot,node1,node2):
if pRoot == None or node1 == None or node2 == None:
return
if node1 < pRoot.data and node2 < pRoot.data:
return self.getLastCommomParent(pRoot.left,node1,node2)
elif node1 > pRoot.data and node2 > pRoot.data:
return self.getLastCommomParent(pRoot.right,node1,node2)
else:
return pRoot测试:
if __name__ == "__main__":
pNode1 = BinarySearchTree(10)
pNode2 = BinarySearchTree(6)
pNode3 = BinarySearchTree(14)
pNode4 = BinarySearchTree(4)
pNode5 = BinarySearchTree(8)
pNode6 = BinarySearchTree(12)
pNode7 = BinarySearchTree(16)
pNode1.left = pNode2
pNode1.right = pNode3
pNode2.left = pNode4
pNode2.right = pNode5
pNode3.left = pNode6
pNode3.right = pNode7
s = Solution()
res = s.getLastCommomParent(pNode1,16,4)
print(res.data)结果:
10情形2、普通树,且有指向父节点的指针
如果树中有指向父节点的指针,那么可以把两个节点到根节点的路径想象成两条链表,那么这个问题可以转化为两个链表的第一个公共节点。
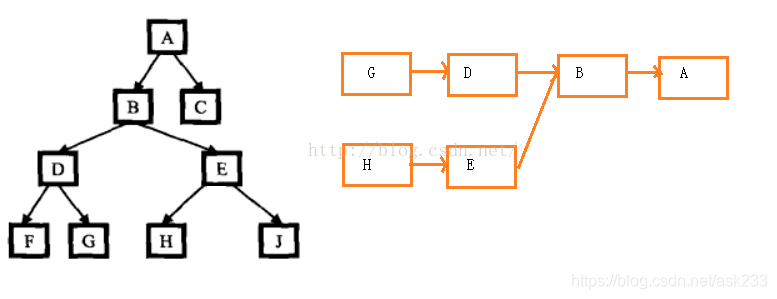
若查找节点G, H的最近公共祖先节点可转化为如图所示的两个链表的交点,可知两节点最近公共祖先节点为B。
class BinaryTree:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
self.parent = None
class Solution2():
'''
二叉树有指向父节点的指针
'''
def getLength(self,pNode):
if pNode == None:
return
length = 0
while pNode:
pNode = pNode.parent
length += 1
return length
def getLastCommomParent2(self,pRoot,pNode1,pNode2):
if pRoot == None or pNode1 == None or pNode2 == None:
return
len1 = self.getLength(pNode1)
len2 = self.getLength(pNode2)
while len1 > len2:
len1 -= 1
pNode1 = pNode1.parent
while len1 < len2:
len2 -= 1
pNode2 = pNode2.parent
while pNode1:
if pNode1 == pNode2:
return pNode1
pNode1 = pNode1.parent
pNode2 = pNode2.parent测试:
if __name__ == "__main__":
'''
二叉树有指向父节点的指针
'''
pNode1 = BinaryTree('A')
pNode2 = BinaryTree('B')
pNode3 = BinaryTree('C')
pNode4 = BinaryTree('D')
pNode5 = BinaryTree('E')
pNode6 = BinaryTree('F')
pNode7 = BinaryTree('G')
pNode8 = BinaryTree('H')
pNode9 = BinaryTree('J')
pNode1.left = pNode2
pNode1.right = pNode3
pNode2.parent = pNode1
pNode3.parent = pNode1
pNode2.left = pNode4
pNode2.right = pNode5
pNode4.parent = pNode2
pNode5.parent = pNode2
pNode4.left = pNode6
pNode4.right = pNode7
pNode6.parent = pNode4
pNode7.parent = pNode4
pNode5.left = pNode8
pNode5.right = pNode9
pNode8.parent = pNode5
pNode9.parent = pNode5
s = Solution2()
res = s.getLastCommomParent2(pNode1,pNode6,pNode5)
print(res.data)结果:
B情形3、普通树,没有指向父节点的指针
方法1、
用两个链表分别保存从根节点到输入的两个节点的路径,然后把问题转换成两个链表的最后公共节点。
时间复杂度:为了得到从根节点开始到输入的两个节点的两条路径,需要遍历两次树,每遍历一次的时间复杂度为O(N),得到两条路径的长度最差的是O(N),通常情况下两条路径是O(lgN)。
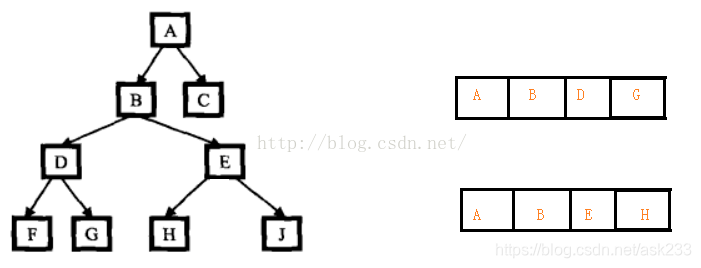
注:下面的getPath函数,并没有把最后的节点放入ret中
F :A->B->D
H:A->B->E
class BinaryTree:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
class Solution2():
'''
普通二叉树中两个结点的最低公共祖先
'''
# 获取结点的路径
def getPath(self, pRoot, pNode, ret):
if pRoot == None or pNode == None:
return False
ret.append(pRoot)
if pRoot == pNode:
return True
left = self.getPath(pRoot.left, pNode, ret)
right = self.getPath(pRoot.right, pNode, ret)
if left or right:
return True
ret.pop()
# 获取公共结点
def getLastCommonNode(self, root, node1, node2):
route1 = []
route2 = [] # 保存结点路径
ret1 = self.getPath(root, node1, route1)
ret2 = self.getPath(root, node2, route2)
ret = None
if ret1 and ret2: # 路径比较
length = len(route1) if len(route1) <= len(route2) else len(route2)
index = 0
while index < length:
if route1[index] == route2[index]:
ret = route1[index]
index += 1
return ret测试:
if __name__ == "__main__":
'''
普通二叉树中两个结点的最低公共祖先
'''
pNode1 = BinaryTree('A')
pNode2 = BinaryTree('B')
pNode3 = BinaryTree('C')
pNode4 = BinaryTree('D')
pNode5 = BinaryTree('E')
pNode6 = BinaryTree('F')
pNode7 = BinaryTree('G')
pNode8 = BinaryTree('H')
pNode9 = BinaryTree('J')
pNode1.left = pNode2
pNode1.right = pNode3
pNode2.left = pNode4
pNode2.right = pNode5
pNode4.left = pNode6
pNode4.right = pNode7
pNode5.left = pNode8
pNode5.right = pNode9
s = Solution2()
res = s.getLastCommonNode(pNode1,pNode6,pNode5)
print(res.data)结果:
B方法2、
(1)如果两个节点分别在根节点的左子树和右子树,则返回根节点
(2)如果两个节点都在左子树,则递归处理左子树;如果两个节点都在右子树,则递归处理右子树
五、二叉树特例—堆
堆分为最大堆和最小堆。在最大堆中根节点的值最大,在最小堆中根节点的值最小。有很多需要快速找到最大值或者最小值的问题都可以用堆来解决。
1.堆的实现
1.1 堆操作
数据结构二叉堆的基本操作定义如下:
- BinaryHeap():创建一个新的空二叉堆对象
- insert(k):加入一个新数据项到堆中
- findMin():返回堆中的最小项,最小项仍保留在堆中
- delMin():返回堆中的最小项,同时从堆中删除
- isEmpty():返回堆是否为空
- size():返回堆中数据项的个数
- buildHeap(list):从一个 key 列表创建新堆
1.2 堆的结构性质
1.2.1 结构:堆应该具有完全树的结构
1、二叉树的操作为对数级
这与上面我们想要用二叉堆降低操作复杂度相吻合。所以用二叉树来实现二叉堆。
2、用完全二叉树将堆操作始终保持在对数水平上。
要想将二叉树的操作保持在对数水平上,我们就需要始终保持二叉树的“平衡”(即左右子树有着相同数量的节点)。因此,我们需要用“完全二叉树”结构来近似的实现“平衡”。
若设二叉树的深度为k,除第k层外,其他各层(1~(k-1)层)的节点数都达到最大值,且第k层所有的节点都连续集中在最左边,这样的树就是完全二叉树
平衡二叉树,又称AVL树,它是一种特殊的二叉搜索树。AVL树或者是一棵空树,或者是具有以下性质的二叉树:
(1)左子树和右子树都是平衡二叉树;
(2)左子树和右子树的深度(高度)之差的绝对值不超过1。
3、完全二叉树可以用列表来实现。
完全树不需要使用节点,引用来实现,因为对于完全树,如果节点在列表中的位置为p,那么其左子节点的位置为2p,类似的,其右子节点的位置为2p+1。
所以对于找任意节点的父节点时,可以直接利用Python的整数除法。若节点在列表中的位置为n,那么父节点的位置是n//2。
下面是完全树的例子以及树的列表表示。
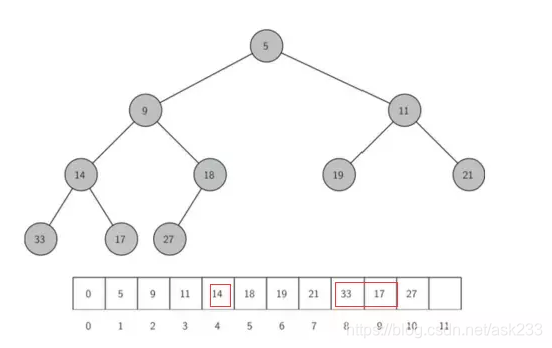
从中可以看出,33和17的父节点,通过n/2即可求得,为14。
1.2.2 性质:堆的次序性
已经解释了二叉堆应该具有什么样的结构(操作复杂度的问题解决了)。那么二叉堆中的数据应该具有什么样的性质呢?
在堆里存储数据项的方法依赖于维持堆次序。所谓堆次序,是指堆中任意一个节点x,其父节点p中的key均小于或等于x中的key。
做个比喻,如果只有完全树的结构,那么优先队列只是拥有了血肉。只能进行复杂度比较低的操作。如果再加上堆次序,那么优先队列就拥有了灵魂,可以在进行复杂度比较低的操作同时,将内在的数据项按照优先级排列。
如上图中的完全树,就是一个具有堆次序的完全树。
2. 堆的操作实现
六、几种树的区别
1.AVL树(平衡二叉树)
(1)简介
AVL树是带有平衡条件的二叉查找树,一般是用平衡因子差值判断是否平衡并通过旋转来实现平衡,左右子树树高不超过1,和红黑树相比,AVL树是严格的平衡二叉树,平衡条件必须满足(所有节点的左右子树高度差不超过1)。不管我们是执行插入还是删除操作,只要不满足上面的条件,就要通过旋转来保持平衡,而的英文旋转非常耗时的,由此我们可以知道AVL树适合用于插入与删除次数比较少,但查找多的情况
(2)局限性
由于维护这种高度平衡所付出的代价比从中获得的效率收益还大,故而实际的应用不多,更多的地方是用追求局部而不是非常严格整体平衡的红黑树。当然,如果应用场景中对插入删除不频繁,只是对查找要求较高,那么AVL还是较优于红黑树。
(3)应用
1,Windows NT内核中广泛存在;
2.红黑树
(1)简介
一种二叉查找树,但在每个节点增加一个存储位表示节点的颜色,可以是红或黑(非红即黑)。通过对任何一条从根到叶子的路径上各个节点着色的方式的限制,红黑树确保没有一条路径会比其它路径长出两倍,因此,红黑树是一种弱平衡二叉树(由于是弱平衡,可以看到,在相同的节点情况下,AVL树的高度低于红黑树),相对于要求严格的AVL树来说,它的旋转次数少,所以对于搜索,插入,删除操作较多的情况下,我们就用红黑树。
(2)性质

如图1所示,每个节点非红即黑;
1. 每个节点非红即黑
2. 根节点是黑的;
3. 每个叶节点(叶节点即树尾端NULL指针或NULL节点)都是黑的;
4. 如图所示,如果一个节点是红的,那么它的两儿子都是黑的;
5. 对于任意节点而言,其到叶子点树NULL指针的每条路径都包含相同数目的黑节点;
6. 每条路径都包含相同的黑节点;
(3)应用
1,广泛用于C ++的STL中,地图和集都是用红黑树实现的;
2,着名的Linux的的进程调度完全公平调度程序,用红黑树管理进程控制块,进程的虚拟内存区域都存储在一颗红黑树上,每个虚拟地址区域都对应红黑树的一个节点,左指针指向相邻的地址虚拟存储区域,右指针指向相邻的高地址虚拟地址空间;
3,IO多路复用的epoll的的的实现采用红黑树组织管理的的的sockfd,以支持快速的增删改查;
4,Nginx的的的中用红黑树管理定时器,因为红黑树是有序的,可以很快的得到距离当前最小的定时器;
5,Java的的的中TreeMap中的中的实现;





 本文围绕树结构展开,先介绍树的基本概念,重点阐述二叉树,包括其遍历方式和常见问题。还探讨了二叉树的特例,如二叉搜索树、堆,介绍它们的概念、操作及常见问题。最后对比了AVL树和红黑树的特点与应用场景。
本文围绕树结构展开,先介绍树的基本概念,重点阐述二叉树,包括其遍历方式和常见问题。还探讨了二叉树的特例,如二叉搜索树、堆,介绍它们的概念、操作及常见问题。最后对比了AVL树和红黑树的特点与应用场景。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








