数组算法精讲-优快云博客

本文深入探讨数组中的经典算法问题，包括查找重复数字、调整数组顺序、寻找中位数及子数组最大和等，提供多种解决方案并分析其时间与空间复杂度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.数组中重复的数字

题目一：

在一个长度为n的数组里的所有数字都在0到n-1的范围内。数组中某些数字是重复的，但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。

例如，如果输入长度为7的数组{2,3,1,0,2,5,3}，那么对应的输出是重复的数字2或者3。

思路：

1、排序

将数组排序，然后扫描排序后的数组即可。

时间复杂度：O(nlogn)，空间复杂度:O(1)

#include <iostream>
#include <algorithm>

using namespace std;

bool duplicate(int numbers[], int length) {
	if (numbers == nullptr || length <= 0)  // * 数组为空
		return false;
	for (int i = 0; i < length; ++i)       //* 数组元素不合法
	{
		if (numbers[i] < 0 || numbers[i]>length - 1)
			return false;
	}
	sort(numbers, numbers + length);

	for (int i = 0; i < length; ++i)
	{
		if (numbers[i] != i)
		{
			cout << "重复元素" << numbers[i] << endl;
			return true;
		}
	}
	return false;
}

int main()
{
	int A[] = { 2,3,1,0,2,5,3 };
	int len = sizeof(A) / sizeof(A[0]);

	duplicate(A, len);

	system("pause");
	return 0;
}

2、哈希表

从头到尾扫描数组，每扫描到一个数字，判断该数字是否在哈希表中，如果该哈希表还没有这个数字，那么加入哈希表，如果已经存在，则返回该数字；

时间复杂度：O(n)，空间复杂度:O(n)

#include <iostream>
#include <unordered_map>

using namespace std;

bool duplicate(int numbers[], int length) {
	if (numbers == nullptr || length <= 0)  // * 数组为空
		return false;
	for (int i = 0; i < length; ++i)       //* 数组元素不合法
	{
		if (numbers[i] < 0 || numbers[i]>length - 1)
			return false;
	}
	unordered_map<int, int> hashmap = {};
	int flag = 0;

	for (int i = 0; i < length; ++i)
	{
		if (hashmap.empty())//判断哈希表是否为空
		{
			hashmap.insert({ numbers[i], numbers[i] });
		}
		else
		{
			for (auto num : hashmap) 
			{  //遍历哈希表
				if (num.first == numbers[i])
				{
					cout << "重复数字:" << numbers[i] << endl;
					flag = 1;
					break;
				}
			}
			if (flag == 1)
				break;
			else
				hashmap.insert({ numbers[i], numbers[i] });
		}
	}
    return false;
}
int main()
{
	int A[] = { 2,3,1,0,2,5,3 };
	int len = sizeof(A) / sizeof(A[0]);

	duplicate(A, len);

	system("pause");
	return 0;
}

3、交换

0~n-1正常的排序应该是A[i]=i；因此可以通过交换的方式，将它们都各自放回属于自己的位置；

从头到尾扫描数组A，当扫描到下标为i的数字m时，首先比较这个数字m是不是等于i，

如果是，则继续扫描下一个数字；

如果不是，则判断它和A[m]是否相等，如果是，则找到了第一个重复的数字（在下标为i和m的位置都出现了m）；如果不是，则把A[i]和A[m]交换，即把m放回属于它的位置；

重复上述过程，直至找到一个重复的数字；

时间复杂度：O(n)，空间复杂度：O(1)

(将每个数字放到属于自己的位置最多交换两次,因此尽管有一个两重循环，总的时间复杂度为O(n))

#include <iostream>

using namespace std;

bool duplicate(int numbers[], int length, int *duplication) {
	if (numbers == nullptr || length <= 0)  // * 数组为空
		return false;
	for (int i = 0; i < length; ++i)       //* 数组元素不合法
	{
		if (numbers[i] < 0 || numbers[i]>length - 1)
			return false;
	}

	for (int i = 0; i < length; ++i)
	{
		while (numbers[i] != i)
		{
			if (numbers[i] == numbers[numbers[i]])
			{
				*duplication = numbers[i];
				return true;
			}
			else //*交换numbers[i] 与 numbers[numbers[i]]
			{
				int temp = numbers[i];
				numbers[i] = numbers[temp];
				numbers[temp] = temp;
			}

		}

	}
	return false;
}

int main()
{
	int A[] = { 2,3,1,0,2,5,3 };
	int len = sizeof(A) / sizeof(A[0]);
	int duplication;
	duplicate(A, len, &duplication);
	cout << duplication << endl;

	system("pause");
	return 0;
}

题目二：

在一个长度为n+1的数组里的所有数字都在1~n的范围内，所以数组中至少有一个数字是重复的。请找出数组中任意一个重复的数字，但是不能修改输入的数组。例如，如果输入长度为8的数组{2,3,5,4,3,2,6,7}，那么对应的输出是重复的数字2或者3。

思路：

1.使用辅助空间

由于不能修改输入的数组，我们可以创建一个长度为n+1的辅助数组，然后逐一把原数组的每个数字复制到辅助数组。如果原数组中被复制的数字是m，则把它复制到辅助数组中下标为m的位置。如果下标为m的位置上已经有数字了，则说明该数字重复了。由于使用了辅助空间，故该方案的空间复杂度是O(n)

#include <iostream>

using namespace std;

bool duplicate(int numbers[], int length, int *duplication) {
	if (numbers == nullptr || length <= 0)  // * 数组为空
		return false;
	for (int i = 0; i < length; ++i)       //* 数组元素不合法
	{
		if (numbers[i] < 0 || numbers[i]>length - 1)
			return false;
	}

	int *tempArry = new int[length];
	for (int i = 0; i < length; ++i)
	{
		if (numbers[i] == tempArry[numbers[i]])
		{
			*duplication = numbers[i];
			return true;
		}
		tempArry[numbers[i]] = numbers[i];
	}
	delete [] tempArry;
	return false;
}

int main()
{
	int A[] = { 2,3,1,0,2,5,3 };
	int len = sizeof(A) / sizeof(A[0]);
	int duplication;
	duplicate(A, len, &duplication);
	cout << duplication << endl;

	system("pause");
	return 0;
}

2.不使用辅助空间

由于思路1的空间复杂度是O(n)，因此我们需要想办法避免使用辅助空间。我们可以这样想：如果数组中有重复的数，那么n+1个1~n范围内的数中，一定有几个数的个数大于1。那么，我们可以利用这个思路解决该问题。

我们把从1~n的数字从中间的数字m分为两部分，前面一半为1~m，后面一半为m+1~n。如果1~m的数字的数目等于m，则不能直接判断这一半区间是否包含重复的数字，反之，如果大于m，那么这一半的区间一定包含重复的数字；如果小于m，另一半m+1~n的区间里一定包含重复的数字。接下来，我们可以继续把包含重复的数字的区间一分为二，直到找到一个重复的数字。

按照二分查找的思路，如果输入长度为n的数组，那么函数countRange将被调用O(log(n))次，每次需要O(n)的时间，因此总的时间复杂度为O(nlog(n))，空间复杂度为O(1)。

#include <iostream>

using namespace std;

int countRange(const int *numbers, int length, int start, int end);

int getDuplication(const int *numbers, int length)
{
	if (numbers == nullptr || length <= 0)
		return -1;

	int start = 1;
	int end = length - 1;
	while (end >= start)
	{
		int middle = ((end - start) >> 1) + start;
		int count = countRange(numbers, length, start, middle);
		if (end == start)
		{
			if (count > 1)
				return start;
			else
				break;
		}

		if (count > (middle - start + 1))
			end = middle;
		else
			start = middle + 1;
	}
	return -1;
}

int countRange(const int *numbers, int length, int start, int end)
{
	if (numbers == nullptr)
		return 0;

	int count = 0;
	for (int i = 0; i < length; ++i)
	{
		if (numbers[i] >= start && numbers[i] <= end)
			++count;
	}
	return count;
}

int main()
{
	int A[] = { 2,3,1,0,2,5,3 };
	int len = sizeof(A) / sizeof(A[0]);

	cout << getDuplication(A, len) << endl;

	system("pause");
	return 0;
}

2.二维数组中的查找

在一个二维数组中，每一行元素都按照从左到右递增的顺序排序，每一列元素都按照从上到下递增的顺序排序。实现一个查找功能的函数，函数的输入为二维数组和一个整数，判断数组中是否含有该整数。

思路

首先选取数组中右上角的数字。如果该数字等于要查找的数字，查找过程结束；如果该数字大于要查找的数字，剔除这个数字所在的列；如果该数字小于要查找的数字，剔除这个数字所在的行。也就是说如果要查找的数字不在数组的右上角，则每一次都在数组的查找范围中剔除一行或者一列，这样每一步都可以缩小查找的范围，直到找到要查找的数字，或者查找范围为空。

例如，我们要在上述的二维数组中查找数字7的步骤如下图所示：

using namespace std;

bool Find(int *matrix, int rows, int columns, int number)
{
	bool found = false;

	if (matrix != nullptr && rows > 0 && columns > 0)
	{
		int row = 0;
		int column = columns - 1;
		while (row < rows && column >= 0)
		{
			if (matrix[row * columns + column] == number)
			{
				found = true;
				break;
			}
			else if (matrix[row * columns + column] > number)
				--column;
			else
				++row;
		}
	}

	return found;
}
int main() {
	int matrix[][4] = { { 1, 2, 8, 9 },{ 2, 4, 9, 12 },{ 4, 7, 10, 13 },{ 6, 8, 11, 15 } };
	//注意(int*)强制转换.相当于将a拉成了一维数组处理。
	bool result = Find((int*) matrix, 4, 4, 7);
	if (result)
		printf("Passed.\n");
	else
		printf("Failed.\n");

	system("pause");
	return 0;
}

3.旋转数组的最小数字

题目：把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。

思路

1、从头到尾遍历数组

从头到尾遍历数组一次，我们就能找出最小的元素。这种思路的时间复杂度显然是O(n)。但是这个思路没有利用输入的旋转数组的特性，肯定达不到面试官的要求。

我们注意到旋转之后的数组实际上可以划分为两个排序的子数组，而且前面的子数组的元素都大于或者等于后面子数组的元素。我们还注意到最小的元素刚好是这两个子数组的分界线。在排序的数组中我们可以用二分查找法实现O(logn)的查找。

2、二分查找

Step1.和二分查找法一样，我们用两个指针分别指向数组的第一个元素和最后一个元素。

Step2.接着我们可以找到数组中间的元素：

　　如果该中间元素位于前面的递增子数组，那么它应该大于或者等于第一个指针指向的元素。此时数组中最小的元素应该位于该中间元素的后面。我们可以把第一个指针指向该中间元素，这样可以缩小寻找的范围。移动之后的第一个指针仍然位于前面的递增子数组之中。如果中间元素位于后面的递增子数组，那么它应该小于或者等于第二个指针指向的元素。此时该数组中最小的元素应该位于该中间元素的前面。当指针指向的数字以及它们的中间数字三者相同时，无法判断数字是位于前面还是后面的子数组，也就无法通过移动指针来缩小查找范围，此时不得不采用顺序查找的方式。

Step3.接下来我们再用更新之后的两个指针，重复做新一轮的查找。

int midInOrder(int *number, int index1, int index2) {
	int result = number[index1];
	for (int i = index1 + 1; i <= index2; ++i)
	{
		if (result > number[i])
			result = number[i];
	}
	return result;
}
int Min(int *number, int length) {
	if (number == nullptr || length <= 0)
		return -1;
	int index1 = 0;
	int index2 = length - 1;
	/*排序数组本身就是一个旋转数组
	因此把nidIndex初始化为index1*/
	int midInex = index1;
	while (number[index1] >= number[index2])
	{
		if (index2 - index1 == 1)
		{
			midInex = index2;
			break;
		}
		midInex = (index1 + index2) / 2;
		/*三个下标指向的数字相同
		只能顺序查找*/
		if (number[index1] == number[index2] && number[index2] == number[midInex])
			return midInOrder(number, index1, index2);
		if (number[midInex] >= number[index1])
			index1 = midInex;
		else if (number[midInex] <= number[index2])
			index2 = midInex;
	}
	return number[midInex];
}

4.调整数组顺序使奇数位于偶数前面

输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有奇数位于数组的前半部分，所有偶数位于数组的后半部分。

思路

1、从头扫描这个数组

如果不考虑时间复杂度，最简单的思路应该是从头扫描这个数组，每碰到一个偶数时，拿出这个数字，并把位于这个数字后面的所有数字往前挪动一位。挪完之后在数组的末尾有一个空位，这时把该偶数放入这个空位。由于每碰到一个偶数就需要移动O(n)个数字，因此总的时间复杂度是O(n^2)。

2、维护两个指针

第一个指针指向第一个数字，它只向后移动，第二个指针指向最后一个数字，它向前移动。如果第一个指针指向偶数且第二个指针指向奇数，则交换两个数字。

void ReorderOddEven(int *number, unsigned length) {
	if (number == nullptr || length <= 0)
		return;
	int *pBegin = number;
	int *pEnd = number + length - 1;
	while (pBegin < pEnd)
	{
		while (pBegin < pEnd && (*pBegin & 0x1) != 0)
			++pBegin;
		while (pBegin < pEnd && (*pEnd & 0x1) == 0)
			--pEnd;
		if (pBegin < pEnd)
		{
			int temp = *pBegin;
			*pBegin = *pEnd;
			*pEnd = temp;
		}
	}
}

可拓展解法

解耦的好处：提高了代码的重用性，为功能拓展提高了便利。

#include <iostream>

void ReorderOddEven(int *number, unsigned length, bool(*func)(int)) {
	if (number == nullptr || length <= 0)
		return;
	int *pBegin = number;
	int *pEnd = number + length - 1;
	while (pBegin < pEnd)
	{
        //向后移动pBegin，直到它指向偶数
		while (pBegin < pEnd && !func(*pBegin))
			++pBegin;
        //向前移动pEnd，直到它指向奇数
		while (pBegin < pEnd && func(*pEnd))
			--pEnd;
		if (pBegin < pEnd)
		{
			int temp = *pBegin;
			*pBegin = *pEnd;
			*pEnd = temp;
		}
	}
}
bool isEven(int n) {
	return (n & 0x1) == 0;
}

void Reorder(int *number, unsigned length) {
	ReorderOddEven(number, length, isEven);
}
int main() {
	int num[] = { 1,2,3,4,5 };
	Reorder(num, 5);
	for (auto i : num)
		std::cout << i;

	system("pause");
	return 0;
}

5.数组中出现次数超过一半的数字

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。如果不存在则输出0。

思路：

方法一：给数组排序

这大概是最直观的方法了，最容易想到，也是最多人能够想出来的。如果我们使用快排的话，只需要O(nlogn)的时间就可以找到这个数。

那么思考这样一个问题：给数组排序了，然后怎么找这个数呢？有两种方法

1、从小到大遍历已排序数组，同时统计每个数出现的次数（某个数和上一个数不同则计数置为1），如果出现某个计数超过一半，那么正在计数的数就是所求数。

PS：这种方法可行，相比于快排的时间复杂度是可以忽略的，但是我们还有更好的方法，直击本质。

2、对一个已排好序的序列，出现次数超过一半的数必定是中位数。因此，我们只要输出中位数即可。

复杂度分析：

时间复杂度	O(nlogn)
空间复杂度	O(n)

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <ctime>
#define RAND(start, end) start+(int)(end-start+1)*rand()/(RAND_MAX+1);
using namespace std;

const int maxn = 10005;

int Partition(int *data, int length, int start, int end)
{
	if (start == end) return start;
	srand((unsigned)time(NULL));
	int index = RAND(start, end);
	swap(data[index], data[end]);
	int one = start - 1;
	for (index = start; index < end; ++index) {
		if (data[index] < data[end]) {
			++one;
			if (one != index) swap(data[one], data[index]);
		}
	}
	++one;
	swap(data[one], data[end]);
	return one;
}

void QuickSort(int *data, int length, int start, int end)
{
	if (length <= 1) return;
	int mid = Partition(data, length, start, end);
	if (mid > start)
		QuickSort(data, length, start, mid - 1);
	if (mid < end)
		QuickSort(data, length, mid + 1, end);
}

int main()
{
	int n, data[maxn];
	cin >> n;
	for (int i = 0; i < n; ++i) {
		cin >> data[i];
	}
	QuickSort(data, n, 0, n - 1);
	cout << data[n >> 1];
}

方法二：找中位数（第n/2大数）

从方法一的分析中我们知道，这个数组的中位数就是答案。方法一是通过给所有的数进行排序找出这个中位数，而我们思考，排序是否有些大材小用？找这个中位数的方法是否可以更简单些？

答案是有的，而且这类问题被称为找第k个数。

思想是快排的思想。时间复杂度为O(n)

利用快排思想，我们可以找出第n/2大的数，同时在第n/2个数左边的数都小于它，右边的数都大于它。这个数就是数组的中位数。

快速排序，利用分治的思想，在数组中随机选择一个数，然后以这个数为基准，把大于它的数划分到它的右侧，小于它的数划分到它的左侧，并且递归的分别对左右两侧数据进行处理，直到所有的区间都按照这样的规律划分好。

那么在这个问题中，如何利用快排的方法呢？快排是对每一个区间进行分治处理，而此问题不必，我们只要找到第n/2小的数。每次随机划分得的第m个数，如果m < n/2, 那么对[m + 1, n - 1]这个区间继续递归；如果m > n/2，那么对[0, m - 1]这个区间进行递归；如果刚好有m = n/2，那么函数结束，区间[0, n/2 - 1]的数就是最小的n/2个数。

此算法的平均时间复杂度为O(n), 快速排序的详细证明可参考“算法导论”。

#include <iostream>
#include <cstdlib>
#include <ctime>
#define RAND(start, end) start + (int)(end - start + 1)*(rand()/(RAND_MAX + 1))

using namespace std;

bool inputInvalid = false;

bool checkInvalidArray(int *numbers, int length) {
	inputInvalid = false;
	if (numbers == nullptr || length < 0)
		inputInvalid = true;
	return inputInvalid;
}

bool checkMoreThanHalf(int *numbers, int length, int number) {
	int times = 0;
	for (int i = 0; i < length; ++i)
	{
		if (numbers[i] == number)
			++times;
	}
	bool moreThanHalf = true;
	if (times * 2 <= length)
	{
		inputInvalid = true;
		moreThanHalf = false;
	}
	return moreThanHalf;
}
int Partition(int *data, int length, int start, int end)
{
	if (start == end) return start;
	srand((unsigned)time(NULL));
	int index = RAND(start, end);
	swap(data[index], data[end]);
	int one = start - 1;
	for (index = start; index < end; ++index) {
		if (data[index] < data[end]) {
			++one;
			if (one != index) swap(data[one], data[index]);
		}
	}
	++one;
	swap(data[one], data[end]);
	return one;
}
int moreThanHalfNum(int *numbers, int length) {
	if (checkInvalidArray(numbers, length))
		return 0;

	int mid = length >> 1;
	int start = 0;
	int end = length - 1;
	int index = Partition(numbers, length, start, end);
	while (index != mid)
	{
		if (index > mid)
		{
			end = mid - 1;
			index = Partition(numbers, length, start, end);
		}
		else
		{
			start = index + 1;
			index = Partition(numbers, length, start, end);
		}
	}
	int result = numbers[mid];
	if (!checkMoreThanHalf(numbers, length, result))
		return 0;
	return result;
}

int main()
{
	int n;
	cin >> n;
	int *data = new int[n];
	for (int i = 0; i < n; ++i) {
		cin >> data[i];
	}
	moreThanHalfNum(data, n, 0, n - 1);

	system("pause");
}

解法三：根据数组特点找出O（n）的算法

接下来我们从另外一个角度来解决这个问题。数组中有一个数字出现的次数超过数组长度的一半，也就是说它出现的次数比其他所有数字出现次数的和还要多。因此我们可以考虑在遍历数组的时候保存两个值：一个是数组中的一个数字，一个是次数。

当我们遍历到下一个数字的时候，如果下一个数字和我们之前保存的数字相同，则次数加1；
如果下一个数字和我们之前保存的数字不同，则次数减1。
如果次数为零，我们需要保存下一个数字，并把次数设为1。

由于我们要找的数字出现的次数比其他所有数字出现的次数之和还要多，那么要找的数字肯定是最后一次把次数设为1时对应的数字。

#include <iostream>

using namespace std;

bool inputInvalid = false;

bool checkInvalidArray(int *numbers, int length) {
	inputInvalid = false;
	if (numbers == nullptr || length < 0)
		inputInvalid = true;
	return inputInvalid;
}
bool checkMoreThanHalf(int *numbers, int length, int number) {
	int times = 0;
	for (int i = 0; i < length; ++i)
	{
		if (numbers[i] == number)
			++times;
	}
	bool moreThanHalf = true;
	if (times * 2 <= length)
	{
		inputInvalid = true;
		moreThanHalf = false;
	}
	return moreThanHalf;
}
int moreThanHalfNum(int *numbers, int length) {
	if (checkInvalidArray(numbers, length))
		return 0;
	int result = numbers[0];
	int times = 1;
	for (int i = 0; i < length; ++i)
	{
		if (times == 0)
		{
			result = numbers[i];
			times = 1;
		}
		else if (numbers[i] == result)
			++times;
		else
			--times;
	}
	if (!checkMoreThanHalf(numbers, length, result))
		return 0;
	return result;
}

int main()
{
	int n;
	cin >> n;
	int *data = new int[n];
	for (int i = 0; i < n; ++i) {
		cin >> data[i];
	}

	cout << moreThanHalfNum(data, n);
	system("pause");
}

6.最小的K个数

输入N个数，找出其中最小的K个数。例如，输入1，2，3，4，5，6，7，8,求最小的4个数，输出1,2,3,4。

思路：

解法一、排序

最直接的想法就是将这些数按照升序排序，然后取前K个数，就是我们最终想要的到的结果，现在较好一点的排序方法时间复杂度是NlogN。

解法二、根据快速思想

对于小规模数据，可以修改输入数组的情况，可以采用类似前题的快速排序思路，pivot之前的点都是比它小的，之后的点都是比它大的。不管是找中位数还是找前k大，前k小，都可以使用这个方法，平均复杂度是O(N),但是最坏时间复杂度是O(N*N)。这样得到最后k个数是没有进行排序的，所以降低了时间复杂度。

#include <iostream>
#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <ctime>
#define RAND(start, end) start+(int)(end-start+1)*rand()/(RAND_MAX+1);

using namespace std;

const int maxn = 10005;

int Partition(int *data, int length, int start, int end)
{
	if (start == end) return start;
	srand((unsigned)time(NULL));
	int index = RAND(start, end);
	swap(data[index], data[end]);
	int one = start - 1;
	for (index = start; index < end; ++index) {
		if (data[index] < data[end]) {
			++one;
			if (one != index) swap(data[one], data[index]);
		}
	}
	++one;
	swap(data[one], data[end]);
	return one;
}

void GetLeastNumbers(int *data, int n, int *output, int k) {
	if (data == nullptr || output == nullptr || n <= 0 || k <= 0)
		return;
	int start = 0;
	int end = n - 1;
	int index = Partition(data, n, start, end);
	while (index != k - 1)
	{
		if (index > k - 1)
		{
			end = index - 1;
			index = Partition(data, n, start, end);
		}
		else
		{
			start = index + 1;
			index = Partition(data, n, start, end);
		}
	}
	for (int i = 0; i < k; ++i)
		output[i] = data[i];	
}
int main() {
	int data[8] = { 4,5,1,6,2,7,3,8 };
	int output[maxn];
	GetLeastNumbers(data, 8, output, 4);
	for (int i = 0; i < 4; ++i)
		cout << output[i] << " ";

	system("pause");
	return 0;
}

解法三、针对处理海量数据的方法，复杂度为O(nlogk）

用容器保存最小的k个数字。每次读入一个数，如果容器中已有的数字少于k个，则直接把这次读入的整数放入容器之中；如果容器中已有k个数字，则比较读入的数字和容器中最大的数字，如果前者大，则在容器中用前者替换后者；如果后者大，则前者不可能是最小的k个数之一，抛弃掉。

容器满了之后，要做3件事：

在K个整数中找到最大值
有可能在这个容器中删除最大值
有可能要插入一个新的数字

如果用二叉树来实现这个容器，能够在O(logK)的时间内实现这3步操作，因此对于n个输入数字，总的时间效率为O(nlogK)。可选用不同的二叉树实现这个容器：

堆

最大的K个数---- 建小堆
最小的K个数----建大堆

#include<iostream>
#include<vector>
using namespace std;

/* 递归方式构建大根堆(len是arr的长度，index是第一个非叶子节点的下标)*/
void adjust(vector<int> &arr, int len, int index)
{
	int left = 2 * index + 1; // index的左子节点
	int right = 2 * index + 2;// index的右子节点

	int maxIdx = index;
	if (left < len && arr[left] > arr[maxIdx])     maxIdx = left;
	if (right < len && arr[right] > arr[maxIdx])     maxIdx = right;

	if (maxIdx != index)
	{
		swap(arr[maxIdx], arr[index]);
		adjust(arr, len, maxIdx);
	}
}
vector<int> GetLeastNumbers(const vector<int> &data, int length, int k) {
	//1.利用前K个数建大堆
	vector<int> result;

	for (int i = 0; i < k; ++i)
		result.push_back(data[i]);
	for (int i = k / 2 - 1; i >= 0; --i)
	{
		adjust(result, k, i);
	}
	//2.遍历后边的数，如果小于堆顶元素则入堆
	for (int i = k; i < length; ++i)
	{
		auto iter = result.begin();
		if (result[0] > data[i])
		{
			auto temp = result.erase(iter);
			result.insert(temp, data[i]);
			adjust(result, k, 0);
		}
	}
	return result;
}
int main() {
	vector<int> data = { 4,5,1,6,2,7,3,8 };

	auto result = GetLeastNumbers(data, 8, 4);
	for (int i = 0; i < 4; ++i)
		cout << result[i] << " ";

	system("pause");
	return 0;
}

红黑树

在STL中，set和multiset都是基于红黑树

#include <iostream>
#include <set>
#include <vector>
#include <functional>

using namespace std;

typedef multiset<int, greater<int>> intSet;

void GetLeastNumbers(const vector<int> &data, intSet &leastNumbers, int k) {
	leastNumbers.clear();
	if (k < 1 || data.size() < k)
		return;
	auto iter = data.begin();
	for (; iter != data.end(); ++iter)
	{
		if (leastNumbers.size() < k)
			leastNumbers.insert(*iter);
		else
		{
			auto iterGreatest = leastNumbers.begin();
			if (*iter < *iterGreatest)
			{
				leastNumbers.erase(iterGreatest);
				leastNumbers.insert(*iter);
			}
		}
	}
}
int main() {
	vector<int> data = { 4,5,1,6,2,7,3,8 };
	intSet result;
	GetLeastNumbers(data, result, 4);
	for (auto i : result)
		cout << i << " ";

	system("pause");
	return 0;
}

7.数据流中的中位数

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。

由于数据是从一个数据流中读出来，因而数据的数目随着时间的增加而增加，如果用一个数据容器来保存从流中读出来的数据，则当新的数据从流中读出来的时候，这些数据就插入数据容器。这个数据用什么数据结构定义合适呢？接下来讨论一下最合适的数据结构：

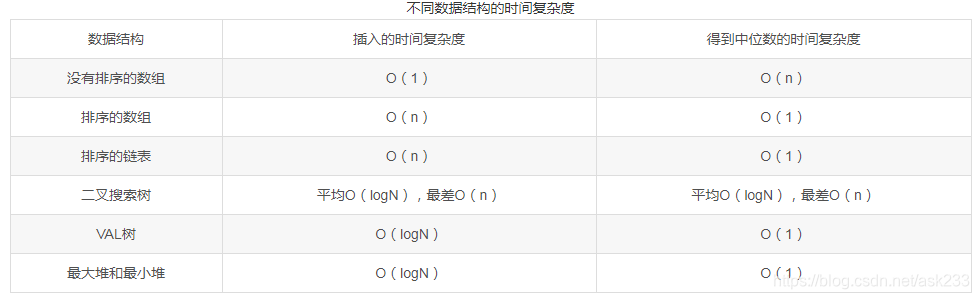
思路：

使容器左边的数都小于右边的数，即使左右两边的数没有排序，也能根据左边最大的数和右边最小的数来实现查中位数。所以左边用大顶锥实现，右边用小顶锥实现。只需要O(1)的时间就可以实现的到顶锥的数据。

如果数据总数目是偶数，插入小顶锥，否则插入大顶锥。要保证大顶锥中的数字都小于小顶锥中的数字，如果是偶数时，插入小顶锥，如果此时的数据比小顶锥中的数据小，怎么办？

解决：

插入小顶锥时，先把数据插入大顶锥，接着把大顶锥中最大数字拿出来插入小顶锥，最终插入的数字就是原大顶锥中最大的数字，这样就保证了小顶锥中的数字都比大顶锥中的数字大。

插入大顶锥与插入小顶锥类似...

#include <iostream>
#include <algorithm>
#include <vector>
#include <functional>

using namespace std;

template <typename T>
class Solution
{
public:
	void insert(T &num);
	T get_num();
private:
	vector<T> min;//右边最小堆--第一个数字最小 
	vector<T> max;//左边最大堆---第一个数字最大 
};
template <typename T>
void Solution<T>::insert(T &num)
{
	if (((min.size() + max.size()) & 1) == 0)//偶数 
	{
		if (max.size() > 0 && num < max[0])
		{
			max.push_back(num);
			push_heap(max.begin(), max.end(), less<T>());//升序 

			num = max[0];

			pop_heap(max.begin(), max.end(), less<T>());//将第一个元素与最以后一个元素替换 
			max.pop_back();//弹出最后一个元素 
		}
		min.push_back(num);
		push_heap(min.begin(), min.end(), greater<T>());//降序 
	}
	else
	{
		if (min.size() > 0 && min[0] < num)
		{
			min.push_back(num);
			push_heap(min.begin(), min.end(), greater<T>());

			num = min[0];

			pop_heap(min.begin(), min.end(), greater<T>());
			min.pop_back();
		}
		max.push_back(num);
		push_heap(max.begin(), max.end(), less<T>());
	}
}
template<typename T>
T Solution<T>::get_num()
{
	int size = max.size() + min.size();
	if (!size)
	{
		cerr << "no number available" << endl;
		return 0x3f3f;
	}
	int mid = 0;
	if (size & 1)
		return min[0];
	else
		return (min[0] + max[0]) / 2;
}
int main()
{
	vector<int> v{ 1,4,9,7,5,6 };
	Solution<int> s;
	for (int i = 0;i < v.size();++i)
	{
		s.insert(v[i]);
	}
	if (s.get_num() != 0x3f3f)
		cout << s.get_num() << endl;
	else
	{
		cerr << "数组有误." << endl;
		return 0;
	}
	return 0;
}

8.连续子数组的最大和

输入一个整型数组，数组里有正数也有负数。数组中一个或连续的多个整数组成一个子数组。求所有子数组的和的最大值。要求时间复杂度为O(n)。例如输入的数组为{1,-2,3,10,-4,7,2,-5}，和最大的子数组为{3,10,-4,7,2}，因此输出为该子数组的和18。

解法一：举例分析数组的规律
例如输入的数组为{1，-2，3，10，-4，7，2，-5}，则计算步骤如下：
1.初始化和 sum sum为0，最大子数组和 resu resu为0，第一步加上数字1， sum sum为1， resu resu为1
2.第二步加上数字-1，和变成了-1，此时最大子数组的大小为第一步中的1，即 resu resu为1，并且-1对之后子数组的和没有帮助，舍弃，即 sum sum归0。
3.第三步加上3， sum sum为3， resu resu为3
4.第四步加上10， sum sum为13， resu resu为13
5.第五步加上-4， sum sum为9，对后面的子数组和有帮助， resu resu仍然为13
6.第六步加上7， sum sum为16， resu resu为16
7.第七步加上2， sum sum为18， resu resu为18
8.第八步加上-5， sum sum为13， resu resu为18
9.结果为18

#include<iostream>

using namespace std;

bool invalidInput = false;
int FindGreatestSumOfSubArray(int arr[], int length) {
	if ((arr == nullptr) || (length <= 0))
	{
		invalidInput = true;
		return 0;
	}
	invalidInput = false;
	int curSum = arr[0];
	int result = arr[0];
	for (int i = 1; i < length; ++i)
	{
		if (curSum <= 0)
			curSum = arr[i];
		else
			curSum += arr[i];
		if (curSum > result)
			result = curSum;
	}
	return result;
}
int main()
{
	int test[]={ 1,-2,3,10,-4,7,2,-5 };

	cout << FindGreatestSumOfSubArray(test, 8) << endl;

	system("pause");
	return 0;
}