树 ( Tree ) 是 n ( n ≥ 0 ) 个结点的有限集。n = 0 时称为空树。
在任意一颗非空树中:
- 有且仅有一个特定的称为 根 ( Root ) 的结点
- 当 n > 1 时,其余结点可分为 m ( m > 0 ) 个互不相交的有限集 T₁ 、 T₂ 、 …… 、Tₘ ,其中每个集合本身又是一棵树,并且称为根的子树 ( SubTree ) 。
- 当 n > 0 时根节点是唯一的,不可能存在多个根结点。
- m > 0 时,子树的个数没有限制,但它们一定是互不相交的。
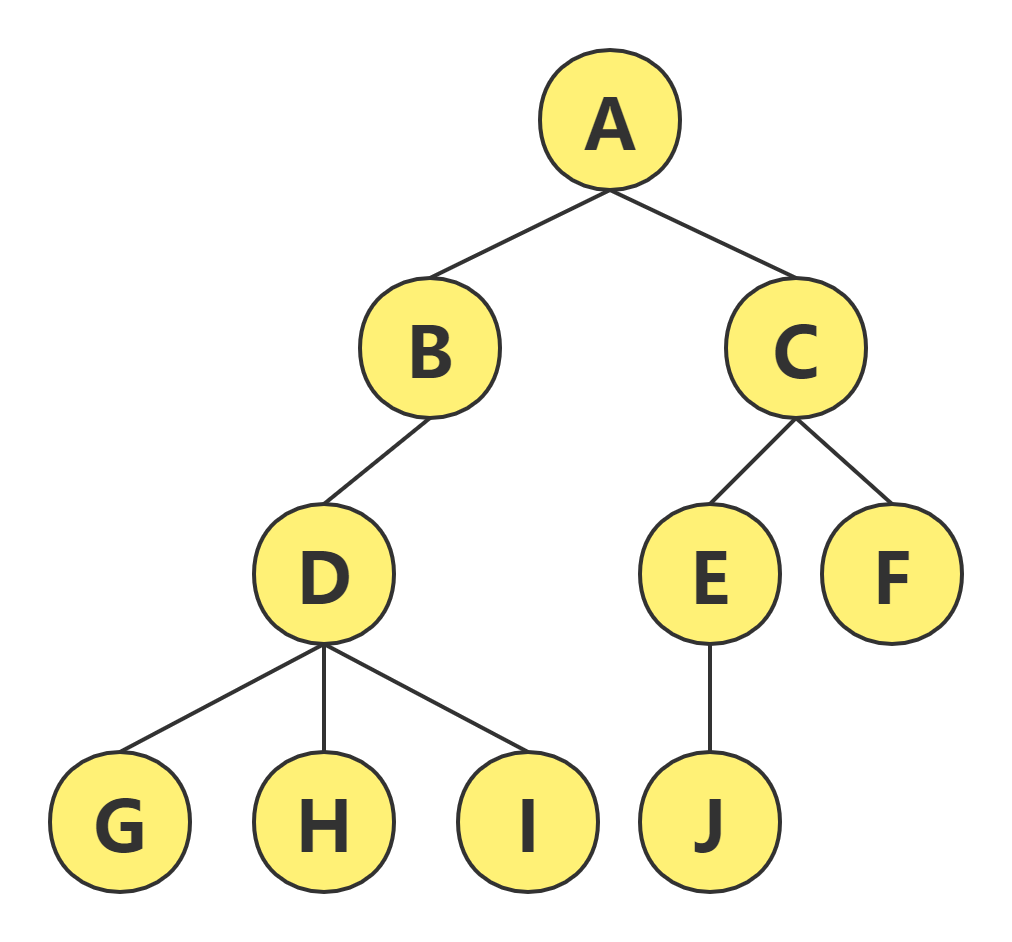
树 ( Tree ) 是 n ( n ≥ 0 ) 个结点的有限集。n = 0 时称为空树。
在任意一颗非空树中:

 7972
7972
 2142
2142
 4452
4452
 3032
3032
 1305
1305
 372
372

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


