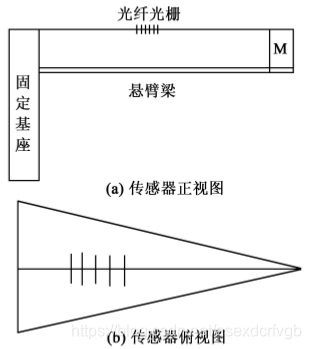
振动传感器示意图
等腰三角形悬臂梁系统参数分析
振动传感器的理论分析 当振动传感器在竖直方向上振动时,由牛顿定律可得
a=FMeff=KeffΔLMeffa=\dfrac{F}{M_{eff}}=\dfrac{K_{eff}\Delta L}{M_{eff}}a=MeffF=MeffKeffΔL
式中:aaa为加速度;FFF为力;ΔL\Delta LΔL为光纤光栅的变化量;MeffM_{eff}Meff为传感系统的等效质量;KeffK_{eff}Keff为传感系统的等效刚度。它们的计算式分别为
Meff=m+13m1M_{eff}=m+\dfrac{1}{3}m_{1}Meff=m+31m1
Keff=bh3E6L3K_{eff}=\dfrac{bh^3E}{6L^3}Keff=6L3bh3E
式中:m1m_1m1为悬臂梁的质量; mmm为质量块的质量;bbb为悬臂梁的底边宽度;LLL为悬臂梁的长度;hhh为悬臂梁的厚度;EEE为弹性模量。 光纤光栅的轴向应变为
ε=ΔLL\varepsilon=\dfrac{\Delta L}{L}ε=LΔL
当作用在光纤光栅中心波长的漂移量满足:
ΔλB=λB(1−Pe)ε\Delta \lambda_{B}=\lambda_B(1-P_{e})\varepsilonΔλB=λB(1−Pe)ε
式中:λB\lambda_{B}λB 为光纤光栅的中心波长;PeP_{e}Pe为光纤的有效弹光系数。
传感器的灵敏度为:
S=ΔλBa=λB(1−Pe)MeffKeffLS=\dfrac{\Delta\lambda_B}{a}=\dfrac{\lambda_B(1-P_e)M_{eff}}{K_{eff}L}S=aΔλB=KeffLλB(1−Pe)Meff
传感器的固有频率为
fn=12πKeffMefff_n=\dfrac{1}{2\pi}\sqrt{\dfrac{K_{eff}}{M_{eff}}}fn=2π1MeffKeff
一、根据结构参数求解固有频率和灵敏度:
首先明确:
重力加速度在SI单位制下的单位是米/秒2米/秒^2米/秒2
牛顿NNN在SI单位制下的单位是加在质量为1kg1kg1kg物体上产生1米/秒21米/秒^21米/秒2的加速度的力为1N1N1N
帕(Pa)在SI单位制下的单位是加在面积为1平方米1平方米1平方米的1N1N1N的力产生1Pa1Pa1Pa的压强
灵敏度在SI单位制下的单位是1米/秒21米/秒^21米/秒2的加速度下产生的单位为pmpmpm位移量
所以,明确我们的结构参数
硅的密度ρ=2328.3kg/m3\rho=2328.3kg/m^3ρ=2328.3kg/m3,弹性模量E=1.9×1011PaE=1.9\times10^{11}PaE=1.9×1011Pa
L=0.035m,b=0.01m,h=0.005mL=0.035m,b=0.01m,h=0.005mL=0.035m,b=0.01m,h=0.005m
m1=L×b×h×ρm1=L\times b \times h\times \rhom1=L×b×h×ρ
m=0.01kgm=0.01kgm=0.01kg
λB=1540462pm\lambda_B=1540462pmλB=1540462pm
光纤的有效弹光系数Pe=0.22P_e=0.22Pe=0.22
光纤光栅的弹性模量E2=0.73PaE_2=0.73PaE2=0.73Pa
由结构参数求解固有频率得:
fn≈48Hzf_n\approx 48Hzfn≈48Hz
S≈376.9pm/gS\approx 376.9pm/gS≈376.9pm/g
二、绘制光谱改变量-激励源频率曲线图
实验中, 固定加速度值,振动台产生10-200hz的激励, 每间隔5Hz改变一次输出频率。这很明显是受迫振动:
由大学物理(杨晓雪)下册第11章可知:
系统在周期性外力的作用下,按外力的周期进行振动,这种振动称为受迫振动,这个周期性外力称为强迫力。假设这个强迫力按余弦规律变化,即:
F(t)=F0coswtF(t)=F_0coswtF(t)=F0coswt
式中,F0F_0F0为强迫力的力幅,www为强迫力的角频率。做受迫振动的系统在弹性力、阻力和强迫力的作用下振动,根据牛顿第二定律,有
md2xdt2=−kx−γdxdt+F0coswtm\dfrac{d^2x}{dt^2}=-kx-\gamma\dfrac{dx}{dt}+F_0coswtmdt2d2x=−kx−γdtdx+F0coswt
令w02=km,2β=γm,f0=F0mw_0^2=\dfrac{k}{m},2\beta=\dfrac{\gamma}{m},f_0=\dfrac{F_0}{m}w02=mk,2β=mγ,f0=mF0,则上式为:
d2xdt2+2βdxdt+w02x=f0coswt\dfrac{d^2x}{dt^2}+2\beta\dfrac{dx}{dt}+w_0^2x=f_0coswtdt2d2x+2βdtdx+w02x=f0coswt
这个微分方程的解为
x=A0e−βtcos(w02−β2t+φ0)+Acos(wt+a)x=A_0e^{-\beta t}cos(\sqrt{w_0^2-\beta^2}t+\varphi_0)+Acos(wt+a)x=A0e−βtcos(w02−β2t+φ0)+Acos(wt+a)
这个解表明,受迫振动可分为两个振动的叠加。第一项表示振动系统最初含有的阻尼振动,这个振动随时间t很快衰减兵小时,所以它对受迫振动的影响是短暂的。第二项则表示一个稳定的谐振动,只要强迫力继续作用,系统就继续做这个振动。经过一段时间后,第一项衰减到可以忽略不计,受迫振动进入稳定的等振幅振动,则表达式为
x=Acos(wt+a)x=Acos(wt+a)x=Acos(wt+a)
上式表明,稳定时受迫振动的频率与强迫力的频率相同。式子中AAA,aaa为受迫振动的振幅和相位,分别为:
A=f0(w02−w2)2+4β2w2A=\dfrac{f_0}{\sqrt{(w_0^2-w^2)^2+4\beta^2w^2}}A=(w02−w2)2+4β2w2f0
a=arctan−2βww02−w2a=arctan\dfrac{-2\beta w}{w_0^2-w^2}a=arctanw02−w2−2βw,可见受迫振动的振幅大小与外力的幅值成正比。
补充:等腰三角形质心的推导:
质心的推导公式:
xc=∫xds∫dsx_c=\dfrac{\int{xds}}{\int{ds}}xc=∫ds∫xds
yc=∫yds∫dsy_c=\dfrac{\int{yds}}{\int{ds}}yc=∫ds∫yds
推导等腰三角形的质心:
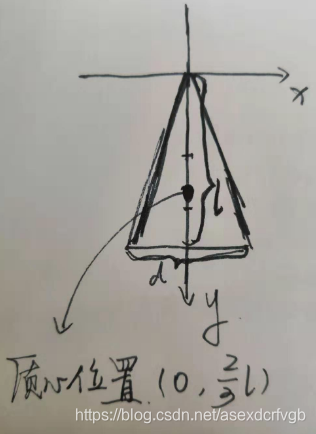
推导:
yc=∫0lyydldy∫0lydldy=∫0ly2dy∫0lydy=y33∣0ly22∣0l=23ly_c=\dfrac{\int_{0}^{l}y\dfrac{yd}{l}dy}{\int_{0}^{l}\dfrac{yd}{l}dy}=\dfrac{\int_0^ly^2dy}{\int_0^lydy}=\dfrac{\dfrac{y^3}{3}|_0^l}{\dfrac{y^2}{2}|_0^l}=\dfrac{2}{3}lyc=∫0llyddy∫0lylyddy=∫0lydy∫0ly2dy=2y2∣0l3y3∣0l=32l




 本文深入探讨了振动传感器的工作原理,通过等腰三角形悬臂梁系统参数分析,详细阐述了传感器的固有频率与灵敏度计算方法,并介绍了受迫振动下的响应特性。
本文深入探讨了振动传感器的工作原理,通过等腰三角形悬臂梁系统参数分析,详细阐述了传感器的固有频率与灵敏度计算方法,并介绍了受迫振动下的响应特性。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








