链表快速排序quick-sort（递归+迭代）

递归版

直接上代码。

static void list_qsort(struct list_head *head)
{
    struct list_head list_less, list_greater;
    struct listitem *pivot;
    struct listitem *item = NULL, *is = NULL;

    if (list_empty(head) || list_is_singular(head))
        return;

    INIT_LIST_HEAD(&list_less);
    INIT_LIST_HEAD(&list_greater);

	//取出第一个节点
    pivot = list_first_entry(head, struct listitem, list);
	//从原链表中删除
    list_del(&pivot->list);

	// item用于遍历， is内部使用的临时变量
    list_for_each_entry_safe (item, is, head, list) {
        if (cmpint(&item->i, &pivot->i) < 0)
            list_move_tail(&item->list, &list_less);
        else
            list_move(&item->list, &list_greater);
    }

    list_qsort(&list_less);
    list_qsort(&list_greater);

    list_add(&pivot->list, head);
    list_splice(&list_less, head);
    list_splice_tail(&list_greater, head);
}


list_add / list_add_tail
将指定的 node 插入 linked list head 的

先将list节点从原链表中删除，然后将这个节点，添加到后边链表的开头/结尾
list_move / list_move_tail

list_splice / list_splice_tail(struct list_head *list, struct list_head *head) (splice拼接)
将 list 的所有 node 都插入到 head 的开头/结尾。注意 list 链表本身仍维持原貌。

 
 

非递归版

原文地址：
https://alienryderflex.com/quicksort/

这篇文章实在太吊了，现简单陈列如下，作者比较了两种版本的实现。
流传甚广的维基百科版：

void swap(int *a, int *b)
{
  int t=*a; *a=*b; *b=t;
}
void sort(int arr[], int beg, int end)
{
  if (end > beg + 1)
  {
    int piv = arr[beg], l = beg + 1, r = end;
    while (l < r)
    {
      if (arr[l] <= piv)
        l++;
      else
        swap(&arr[l], &arr[--r]);
    }
    swap(&arr[--l], &arr[beg]);
    sort(arr, beg, l);
    sort(arr, r, end);
  }
}
作者说，把swap加上inline关键字，可以减少调用函数的栈开支。

作者自己的版本：

//  quickSort
//
//  This public-domain C implementation by Darel Rex Finley.
//
//  * Returns YES if sort was successful, or NO if the nested
//    pivots went too deep, in which case your array will have
//    been re-ordered, but probably not sorted correctly.
//
//  * This function assumes it is called with valid parameters.
//
//  * Example calls:
//    quickSort(&myArray[0],5); // sorts elements 0, 1, 2, 3, and 4
//    quickSort(&myArray[3],5); // sorts elements 3, 4, 5, 6, and 7

bool quickSort(int *arr, int elements) {

  #define  MAX_LEVELS  1000

  int  piv, beg[MAX_LEVELS], end[MAX_LEVELS], i=0, L, R ;

  beg[0]=0; end[0]=elements;
  while (i>=0) {
    L=beg[i]; R=end[i]-1;
    if (L<R) {
      piv=arr[L]; if (i==MAX_LEVELS-1) return NO;
      while (L<R) {
        while (arr[R]>=piv && L<R) R--; if (L<R) arr[L++]=arr[R];
        while (arr[L]<=piv && L<R) L++; if (L<R) arr[R--]=arr[L]; }
      arr[L]=piv; beg[i+1]=L+1; end[i+1]=end[i]; end[i++]=L; }
    else {
      i--; }}
  return YES; }

Advantages of my code over the Wikipedia code: 优势

1. FUNCTION CALLS My implementation avoids function calls. Calling (and returning from) a function is time-consuming, and not because the content of the function takes time to execute — just getting into the function, and back out of it, uses processor time.

2. STACK My implementation does not use the stack to store data. Recursive functions look neat and simple in part because they don’t have to have big arrays like my beg[] and end[]. But all they’re really doing is using the stack as their own private array. This is much slower than using a real array, and could cause stack overflow on some systems, crashing the app that called the quicksort. My implementation simply returns NO if this kind of failure occurs.

3. SWAP VARIABLE In any one pivot round, the Wikipedia version can pass items through a swap variable many times. My code passes only one item (the pivot) through a swap variable, and only once per round.

4. MULTIPLE MOVES In any one pivot round, the Wikipedia version can move the same item more than once in the list. My code never moves an item to a new position in the list more than once per round.

5. UNNECESSARY MOVES In any one pivot round, the Wikipedia version will sometimes move items to new positions in the list even though they were already on the correct side of where the pivot item was going to wind up. My code never moves an item if its current position is on the correct side of the pivot’s destination.

6. SELF-SWAPS In each pivot round, the Wikipedia version has about a 50% chance of swapping one of the list items with itself. (And this swap incurs the costs described above in #1, #2, and #3.)

(Note that the benefits of all six advantages are greatly increased if the items being sorted are substantially sized data structures, as opposed to simple integers as in these code examples.)

Limitations of my code vs. the Wiki code:劣势

1. COMPARISONS My code performs more comparisons, on average, than the Wiki version. Wiki does 30% fewer comparisons by my (very rough) estimate.

 
 
非常给力的图示来了，
作者自己的版本：

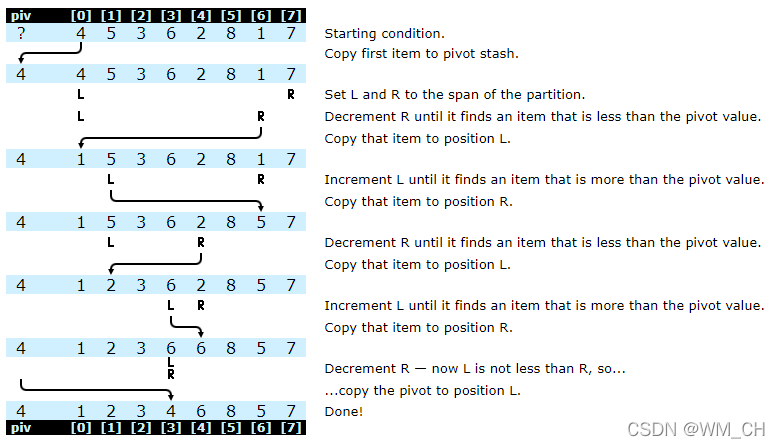
数字 3, 8, 7 没有动位置. 其他数字只移动了一次，而且和 pivot（支点） 只比较了一次。
维基百科版：

在数据值3、8和7中(它们都不需要移动的)，只有3没动，8被移动了两次。Swap 变量被使用了五次。

 
 
最后作者又来了一个无敌版，从来不会失败的版本（永远都不会跑到 MAX_LEVELS ）：

//  quickSort
//
//  This public-domain C implementation by Darel Rex Finley.
//
//  * This function assumes it is called with valid parameters.
//
//  * Example calls:
//    quickSort(&myArray[0],5); // sorts elements 0, 1, 2, 3, and 4
//    quickSort(&myArray[3],5); // sorts elements 3, 4, 5, 6, and 7

void quickSort(int *arr, int elements) {

  #define  MAX_LEVELS  300

  int  piv, beg[MAX_LEVELS], end[MAX_LEVELS], i=0, L, R, swap ;

  beg[0]=0; end[0]=elements;
  while (i>=0) {
    L=beg[i]; R=end[i]-1;
    if (L<R) {
      piv=arr[L];
      while (L<R) {
        while (arr[R]>=piv && L<R) R--; if (L<R) arr[L++]=arr[R];
        while (arr[L]<=piv && L<R) L++; if (L<R) arr[R--]=arr[L]; }
      arr[L]=piv; beg[i+1]=L+1; end[i+1]=end[i]; end[i++]=L;
      if (end[i]-beg[i]>end[i-1]-beg[i-1]) {
        swap=beg[i]; beg[i]=beg[i-1]; beg[i-1]=swap;
        swap=end[i]; end[i]=end[i-1]; end[i-1]=swap; }}
    else {
      i--; }}}

This might be slightly slower than the first one, but it will never fail because it always performs the smaller partition first. Hence, the only way it could run into the limit is if the to-be-sorted array was at least 2^MAX_LEVELS elements in size. Since 2^300 is greater than 10^90, and there are only about 1080 fundamental particles in this universe from which a human-made computer can be built, no larger limit will ever be needed.

(Note: Someone reminded me that a typically 64-bit index variable can index only 2^64 items, not 2^300. That’s true, but if you’re using a 64-bit computer, you’re probably not going to have an array of more than 2^64 elements anyway, even if each element was only one byte.)

------------------回到我们讨论的非递归版本的快速排序----------------------
直接看代码：

static void list_qsort_no_recursive(struct list_head *head) {
    struct listitem *begin[MAX_LEN], *end[MAX_LEN], *L, *R;
    struct listitem pivot;
    int i = 0;

    begin[0] = list_first_entry(head, struct listitem, list);
    end[0] = list_last_entry(head, struct listitem, list);
    while (i >= 0) {
        L = begin[i];
        R = end[i];
        if (L != R && &begin[i]->list != head) {
            // pivot is the actual address of L
            pivot = *begin[i];
            if (i == MAX_LEN - 1) {
                assert(-1);
                return;
            }
            while (L != R) {
                while (R->i >= pivot.i && L != R)
                    R = list_entry(R->list.prev, struct listitem, list);
                if (L != R) {
                    L->i = R->i;
                    L = list_entry(L->list.next, struct listitem, list);
                }

                while (L->i <= pivot.i && L != R)
                    L = list_entry(L->list.next, struct listitem, list);
                if (L != R) {
                    R->i = L->i;
                    R = list_entry(R->list.prev, struct listitem, list);
                }
            }
            L->i = pivot.i;
            begin[i + 1] = list_entry(L->list.next, struct listitem, list);
            end[i + 1] = end[i];
            end[i++] = L;
        } else
            i--;
    }
}

 
 
完。