A. 升序序列
题面
给定一个长度为 N N N 的正整数序列 A 1 , A 2 , … , A N A_1, A_2, \dots, A_N A1,A2,…,AN。现在希望将该序列变为升序排列。所谓升序排列,是指对于所有的 i i i( 1 ≤ i ≤ N − 1 1 \leq i \leq N - 1 1≤i≤N−1),都有 A i ≤ A i + 1 A_i \leq A_{i+1} Ai≤Ai+1。
为了将序列 A A A 排成升序,可以对序列执行以下操作若干次(可为零次):
- 对于某个 i i i( 1 ≤ i ≤ N 1 \leq i \leq N 1≤i≤N),将 A i A_i Ai 乘以 2 2 2。
你的任务是以最小的操作次数将序列 A A A 排成升序,并输出所需的最小操作次数。
输入格式
第一行输入一个整数
N
N
N。
第二行输入
N
N
N 个整数,表示
A
1
,
A
2
,
…
,
A
N
A_1, A_2, \dots, A_N
A1,A2,…,AN,以空格分隔。
输出格式
输出一个整数,表示将序列变为升序所需的最小操作次数。
输入输出样例 #1
输入 #1
5
3 1 4 1 5
输出 #1
4
输入输出样例 #2
输入 #2
5
3 1 5 1 5
输出 #2
6
输入输出样例 #3
输入 #3
5
1 2 3 4 5
输出 #3
0
说明/提示
样例 1 说明
对 A 2 A_2 A2 和 A 4 A_4 A4 各执行两次操作后,序列变为 [ 3 , 4 , 4 , 4 , 5 ] [3, 4, 4, 4, 5] [3,4,4,4,5]。
样例 2 说明
对 A 2 A_2 A2 操作两次, A 4 A_4 A4 操作三次, A 5 A_5 A5 操作一次,最终序列为 [ 3 , 4 , 5 , 8 , 10 ] [3, 4, 5, 8, 10] [3,4,5,8,10]。
约束条件
- 所有给定的数均为整数。
- 1 ≤ N ≤ 250 000 1 \leq N \leq 250\,000 1≤N≤250000
- 1 ≤ A i ≤ 1 000 000 1 \leq A_i \leq 1\,000\,000 1≤Ai≤1000000,其中 1 ≤ i ≤ N 1 \leq i \leq N 1≤i≤N
子问题
- (12 分)对于所有 i i i( 1 ≤ i ≤ N 1 \leq i \leq N 1≤i≤N), A i = 1 A_i = 1 Ai=1 或 A i = 2 A_i = 2 Ai=2
- (10 分)对于所有 i i i( 1 ≤ i ≤ N 1 \leq i \leq N 1≤i≤N),存在非负整数 k i k_i ki,使得 A i = 2 k i A_i = 2^{k_i} Ai=2ki
- (11 分) N ≤ 10 N \leq 10 N≤10
- (19 分)对于所有 i i i( 1 ≤ i ≤ N 1 \leq i \leq N 1≤i≤N), A i = 2 A_i = 2 Ai=2 或 A i = 3 A_i = 3 Ai=3
- (20 分)对于所有 i i i( 1 ≤ i ≤ N − 1 1 \leq i \leq N - 1 1≤i≤N−1), A i ≥ A i + 1 A_i \geq A_{i+1} Ai≥Ai+1
- (28 分)无额外限制条件
思路
暴力
首先想到暴力
显然,如果出了这种数据,就会爆long long
1000000 999999 999998 ···
数值接近成倍增加,开了long long还是见祖宗
优化
可以想到用科学计数法
代码思路:
- 对每个数取以 2 为底的对数,这样 “乘以 2” 的操作就转化为 “加 1” 的操作
- 从左到右遍历序列,确保每个元素的对数值(加上乘法次数)不小于前一个元素的对数值
- 计算需要增加的次数(即需要乘以 2 的次数)并累加
代码
#include<bits/stdc++.h>
using namespace std;
// 处理浮点数精度问题的小量
const double EPS = 1e-10;
int main() {
int n;
cin >> n;
long long total_ops = 0;
// 存储上一个元素经过乘法操作后的log2值
double prev_log = 0.0;
for (int i = 0; i < n; ++i) {
int x;
cin >> x;
// 计算当前元素的log2值
double curr_log = log2(x);
// 如果是第一个元素,直接设置为参考值
if (i == 0) {
prev_log = curr_log;
continue;
}
// 当前元素的log值小于前一个元素的log值,需要乘以2
if (curr_log < prev_log - EPS) {
// 计算需要乘以2的次数(向上取整)
double diff = prev_log - curr_log;
long long k = (long long)ceil(diff - EPS);
total_ops += k;
// 更新当前元素经过k次乘法后的log值
curr_log += k;
}
// 更新参考值为当前元素的log值
prev_log = curr_log;
}
cout << total_ops;
return 0;
}
B. 最大与求和
题面
无向连通图 G G G 有 n n n 个点, n − 1 n-1 n−1 条边。点从 1 1 1 到 n n n 依次编号,编号为 i i i 的点的权值为 W i W_i Wi,每条边的长度均为 1 1 1。图上两点 ( u , v ) (u, v) (u,v) 的距离定义为 u u u 点到 v v v 点的最短距离。对于图 G G G 上的点对 ( u , v ) (u, v) (u,v),若它们的距离为 2 2 2,则它们之间会产生 W v × W u W_v \times W_u Wv×Wu 的联合权值。
请问图 G G G 上所有可产生联合权值的有序点对中,联合权值最大的是多少?所有联合权值之和是多少?
输入格式
第一行包含 1 1 1 个整数 n n n。
接下来 n − 1 n-1 n−1 行,每行包含 2 2 2 个用空格隔开的正整数 u , v u,v u,v,表示编号为 u u u 和编号为 v v v 的点之间有边相连。
最后 1 1 1 行,包含 n n n 个正整数,每两个正整数之间用一个空格隔开,其中第 i i i 个整数表示图 G G G 上编号为 i i i 的点的权值为 W i W_i Wi。
输出格式
输出共 1 1 1 行,包含 2 2 2 个整数,之间用一个空格隔开,依次为图 G G G 上联合权值的最大值和所有联合权值之和。由于所有联合权值之和可能很大,输出它时要对 10007 10007 10007 取余。
输入输出样例 #1
输入 #1
5
1 2
2 3
3 4
4 5
1 5 2 3 10
输出 #1
20 74
说明/提示
样例解释
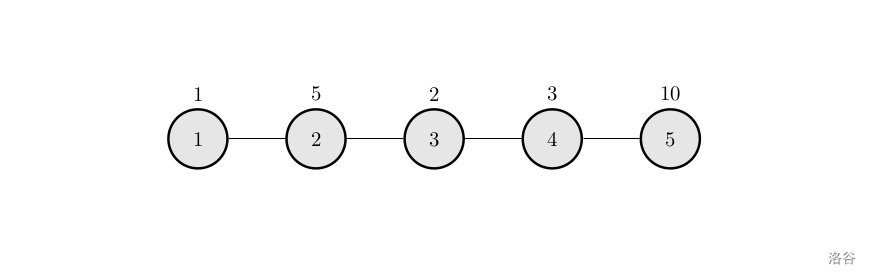
本例输入的图如上所示,距离为 2 2 2 的有序点对有 ( 1 , 3 ) (1,3) (1,3) 、 ( 2 , 4 ) (2,4) (2,4) 、 ( 3 , 1 ) (3,1) (3,1) 、 ( 3 , 5 ) (3,5) (3,5)、 ( 4 , 2 ) (4,2) (4,2) 、 ( 5 , 3 ) (5,3) (5,3)。
其联合权值分别为 2 , 15 , 2 , 20 , 15 , 20 2,15,2,20,15,20 2,15,2,20,15,20。其中最大的是 20 20 20,总和为 74 74 74。
数据说明
- 对于 30 % 30\% 30% 的数据, 1 < n ≤ 100 1 < n \leq 100 1<n≤100;
- 对于 60 % 60\% 60% 的数据, 1 < n ≤ 2000 1 < n \leq 2000 1<n≤2000;
- 对于 100 % 100\% 100% 的数据, 1 < n ≤ 2 × 10 5 1 < n \leq 2\times 10^5 1<n≤2×105, 0 < W i ≤ 10000 0 < W_i \leq 10000 0<Wi≤10000。
保证一定存在可产生联合权值的有序点对。
思路
关键洞察
距离为 2 的点对必然有一个共同的中间节点。也就是说,对于任意两个节点 u 和 v,如果它们之间的距离为 2,那么存在一个节点 w,使得:
- u 和 w 相连
- v 和 w 相连
- u ≠ v
因此,我们可以遍历每个节点作为中间节点,考虑它的所有邻居节点之间的配对。
-
图表示:使用邻接表存储树结构
-
遍历中间节点:对于每个节点 u,如果它有至少 2 个邻居
-
处理邻居节点:
- 最大值计算:找出 u 的邻居中权值最大的两个节点,它们的乘积可能是候选最大值
- 总和计算:计算所有邻居节点两两配对的权值乘积之和
-
数学优化:
对于总和计算,使用数学恒等式:
- 所有有序点对 (v, w) 的权值乘积之和 = (所有邻居权值之和)2 - 所有邻居权值平方之和
- 这是因为: ( ∑ w i ) 2 = ∑ w i 2 + 2 ∑ i ≠ j w i w j \left(\sum w_i\right)^2 = \sum w_i^2 + 2\sum_{i \neq j} w_i w_j (∑wi)2=∑wi2+2i=j∑wiwj
代码
#include<bits/stdc++.h>
using namespace std;
const int MOD = 10007;
const int MAXN = 200005;
vector<int> graph[MAXN];
long long w[MAXN];
int main() {
int n;
cin >> n;
for (int i = 0; i < n - 1; i++) {
int u, v;
cin >> u >> v;
graph[u].push_back(v);
graph[v].push_back(u);
}
for (int i = 1; i <= n; i++) {
cin >> w[i];
}
long long max_val = 0;
long long total_sum = 0;
for (int u = 1; u <= n; u++) {
if (graph[u].size() < 2) continue;
long long sum = 0;
long long sum_sq = 0;
long long max1 = 0, max2 = 0;
for (int v : graph[u]) {
sum = (sum + w[v]) % MOD;
sum_sq = (sum_sq + w[v] * w[v]) % MOD;
if (w[v] > max1) {
max2 = max1;
max1 = w[v];
}
else if (w[v] > max2) {
max2 = w[v];
}
}
max_val = max(max_val, max1 * max2);
total_sum = (total_sum + (sum * sum - sum_sq) % MOD) % MOD;
}
cout << max_val << " " << total_sum % MOD << endl;
return 0;
}
C. 子串
题面
给定一个由小写英文字母组成、长度为 N N N 的字符串 S S S,以及 Q Q Q 个查询。请依次处理这些查询。
查询有以下两种类型:
1 x c:将 S S S 的第 x x x 个字符替换为字符 c c c。2 l r:将 S S S 按照字符的升序排列得到字符串 T T T。如果 S S S 的第 l l l 个字符到第 r r r 个字符组成的子串是 T T T 的子串,则输出Yes,否则输出No。
什么是子串?
S
S
S 的子串是指从
S
S
S 的开头删除
0
0
0 个或多个字符、从末尾删除
0
0
0 个或多个字符后得到的字符串。例如,ab 是 abc 的子串,但 ac 不是 abc 的子串。
输入格式
输入按以下格式从标准输入给出。其中, query i \text{query}_i queryi 表示第 i i i 个查询。
N N N S S S Q Q Q
query 1 \text{query}_1 query1
query 2 \text{query}_2 query2
⋮ \vdots ⋮
query Q \text{query}_Q queryQ
输出格式
请按照题目要求依次处理每个查询。
输入输出样例 #1
输入 #1
6
abcdcf
4
2 1 3
2 2 6
1 5 e
2 2 6
输出 #1
Yes
No
Yes
说明/提示
限制条件
- 1 ≤ N ≤ 10 5 1 \leq N \leq 10^5 1≤N≤105
- S S S 是由小写英文字母组成的长度为 N N N 的字符串
- 1 ≤ Q ≤ 10 5 1 \leq Q \leq 10^5 1≤Q≤105
- 对于第 1 种类型的查询, 1 ≤ x ≤ N 1 \leq x \leq N 1≤x≤N
- 对于第 1 种类型的查询, c c c 是小写英文字母
- 对于第 2 种类型的查询, 1 ≤ l ≤ r ≤ N 1 \leq l \leq r \leq N 1≤l≤r≤N
样例解释 1
- 对于第 1 个查询,将
S
S
S 按字符升序排列得到的字符串
T
T
T 是
abccdf。 S S S 的第 1 1 1 到第 3 3 3 个字符组成的字符串是abc,它是 T T T 的子串,因此输出Yes。 - 对于第 2 个查询,将
S
S
S 按字符升序排列得到的字符串
T
T
T 是
abccdf。 S S S 的第 2 2 2 到第 6 6 6 个字符组成的字符串是bcdcf,它不是 T T T 的子串,因此输出No。 - 第 3 个查询将
S
S
S 的第
5
5
5 个字符替换为
e,此时 S S S 变为abcdef。 - 对于第 4 个查询,将
S
S
S 按字符升序排列得到的字符串
T
T
T 是
abcdef。 S S S 的第 2 2 2 到第 6 6 6 个字符组成的字符串是bcdef,它是 T T T 的子串,因此输出Yes。
思路
啊!我考试时写的暴力样例都过了,竟然一分也没拿,数据太欺负人了。

那么现在请欣赏我的零分代码:
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
string s;
cin>>s;
int q;
cin>>q;
while(q--){
int y;
cin>>y;
if(y==1){
int x;
char c;
cin>>x>>c;
s[x-1]=c;
}
else{
int l,r;
cin>>l>>r;
l--,r--;
string t=s;
sort(t.begin(),t.end());
bool flag=true;
for(int i=0;i<t.size()-(r-l);i++){
flag=true;
if(s[l]!=t[i])continue;
for(int j=l+1,yy=i+1;j<=r;j++,yy++){
if(s[j]!=t[yy]){
flag=false;
break;
}
}
if(flag==true)break;
}
if(flag)cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
}
return 0;
}
好了,不闹了,还是讲正解吧。
你想看的正解:
充要条件
对于查询 2 l r,S[l..r] 是排序后字符串 T 的子串当且仅当:
- 非递减性:
S[l..r]是非递减的 - 字符连续性:对于所有字符
x满足min_char < x < max_char,x在S[l..r]中的出现次数等于它在整个字符串中的出现次数
高效维护
-
非递减性检查:
- 定义差分数组:
d[i] = |S[i] - S[i-1]|(对于i ≥ 2) S[l..r]非递减 ?sum(d[l+1..r]) = S[r] - S[l]- 用 Fenwick Tree 维护
d[i]的前缀和
- 定义差分数组:
-
字符计数:
- 用 26 个 Fenwick Tree 维护每个字母的出现次数
- 维护全局计数数组
tot[26]
-
修改操作:
- 更新字符计数:旧字符减1,新字符加1
- 更新差分数组:修改位置
x会影响d[x]和d[x+1]
好了,最后上代码。
代码
提前声明:码量大,请原谅。
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
// Fenwick Tree 模板
template<typename T>
struct Fenw {
int n;
vector<T> tree;
Fenw(int n) : n(n), tree(n + 1) {}
void update(int i, T val) {
for (; i <= n; i += i & -i) {
tree[i] += val;
}
}
T query(int i) {
T res = 0;
for (; i > 0; i -= i & -i) {
res += tree[i];
}
return res;
}
T query(int l, int r) {
return query(r) - query(l - 1);
}
};
int n, q;
string s;
Fenw<int> *d_tree; // 维护差分绝对值
Fenw<int> *char_trees[26]; // 26个字符的计数树
int tot[26]; // 全局字符计数
int a[N]; // 字符数值表示
// 初始化
void init() {
cin >> n >> s >> q;
s = " " + s;
// 初始化 Fenwick Trees
d_tree = new Fenw<int>(n);
for (int i = 0; i < 26; i++) {
char_trees[i] = new Fenw<int>(n);
}
// 初始化数组和树
for (int i = 1; i <= n; i++) {
a[i] = s[i] - 'a';
tot[a[i]]++;
char_trees[a[i]]->update(i, 1);
if (i > 1) {
int diff = abs(a[i] - a[i-1]);
d_tree->update(i, diff);
}
}
}
// 处理修改操作
void handle_update(int x, char c_char) {
int new_char = c_char - 'a';
int old_char = a[x];
if (old_char == new_char) return;
// 更新全局计数
tot[old_char]--;
tot[new_char]++;
// 更新字符计数树
char_trees[old_char]->update(x, -1);
char_trees[new_char]->update(x, 1);
// 更新差分数组(影响位置 x 和 x+1)
if (x > 1) {
int old_diff = abs(a[x] - a[x-1]);
int new_diff = abs(new_char - a[x-1]);
d_tree->update(x, new_diff - old_diff);
}
if (x < n) {
int old_diff = abs(a[x+1] - a[x]);
int new_diff = abs(a[x+1] - new_char);
d_tree->update(x + 1, new_diff - old_diff);
}
a[x] = new_char;
s[x] = c_char;
}
// 处理查询操作
bool handle_query(int l, int r) {
if (l == r) return true; // 单字符总是非递减
// 检查非递减性
int expected_diff = a[r] - a[l];
int actual_diff_sum = d_tree->query(l + 1, r);
if (actual_diff_sum != expected_diff) {
return false;
}
// 检查字符连续性
int min_char = 26, max_char = -1;
for (int c = 0; c < 26; c++) {
int cnt = char_trees[c]->query(l, r);
if (cnt > 0) {
min_char = min(min_char, c);
max_char = max(max_char, c);
}
}
for (int c = min_char + 1; c < max_char; c++) {
int seg_cnt = char_trees[c]->query(l, r);
if (seg_cnt != tot[c]) {
return false;
}
}
return true;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
init();
while (q--) {
int type;
cin >> type;
if (type == 1) {
int x; char c;
cin >> x >> c;
handle_update(x, c);
}
else {
int l, r;
cin >> l >> r;
cout << (handle_query(l, r) ? "Yes\n" : "No\n");
}
}
// 释放内存
delete d_tree;
for (int i = 0; i < 26; i++) {
delete char_trees[i];
}
return 0;
}
时间复杂度: O ( Q × ( 26 + l o g N ) ) O(Q×(26 + log N)) O(Q×(26+logN))
D. 三色划分
思路
这是不是你的第一眼思路(好吧,是我的):
这不就是简单地 D F S DFS DFS 吗,随手做。
七分钟后打出了这样的代码:
#include<bits/stdc++.h>
using namespace std;
int n,a[305],maxn,ans,r,g,b;
void dfs(int x){
if(x==n+1){
if(r!=0&&g!=0&&b!=0){
if(r+g>b&&r+b>g&&g+b>r)
ans++;
}
return;
}
if(r+a[x]<=maxn){
r+=a[x];
dfs(x+1);
r-=a[x];
}
if(g+a[x]<=maxn){
g+=a[x];
dfs(x+1);
g-=a[x];
}
if(b+a[x]<=maxn){
b+=a[x];
dfs(x+1);
b-=a[x];
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
maxn+=a[i];
}
maxn=(maxn-1)/2;
dfs(1);
cout<<ans;
return 0;
}
获得成就:TLE
好了,写完 DFS 之后就知道要用 DP 了。
正难则反才是进步的过程。
1. 正难则反
直接计算满足条件的方案数比较困难,我们采用容斥原理:
- 总方案数:3?(每个数有3种选择)
- 减去不满足条件的方案数
- 得到满足条件的方案数
2. 三角形条件
三个正数 R, G, B 能构成三角形的充要条件是:
R + G > B
R + B > G
G + B > R
这个条件等价于:
R, G, B < (R + G + B) / 2
设总和 S = R + G + B,则条件为:
R < S/2, G < S/2, B < S/2
3. 不合法的情况
不合法的情况就是至少有一个颜色的和 ≥ S/2(上取整)。由于三个数的和为S,最多只能有一个颜色的和 ≥ S/2(否则两个颜色的和就会超过S,矛盾)。
4. 计算不合法方案数
对于每种颜色(红、绿、蓝),计算该颜色的和 ≥ S/2 的方案数。由于三种颜色对称,我们只需要计算一种颜色,然后乘以3。
红色不合法方案数计算:
使用动态规划(背包):
f[j]:红色和为 j 的方案数- 对于每个数,有三种选择:
- 染红色:贡献 a?
- 染绿色:不贡献(但有两种选择:绿或蓝)
- 染蓝色:不贡献
状态转移方程:
f[j] = 2 × f[j] + f[j - a?]
5. 去重处理
当 S 为偶数时,可能存在 R = G = S/2 的情况,这种情况在计算红色和绿色不合法时被重复计算了两次,需要减去。
使用另一个DP数组 g[j] 来计算红色和恰好为 j 的方案数(用于去重)。
算法步骤
- 计算总方案数:3?
- 初始化DP数组:
f[0] = 1,g[0] = 1 - 动态规划:
- 对于每个数,更新
f数组(至少装满) - 对于每个数,更新
g数组(恰好装满)
- 对于每个数,更新
- 计算不合法方案数:
- 红色不合法:∑f[j],其中 j ≥ ?S/2?
- 乘以3(三种颜色对称)
- 减去重复计算的部分(如果S为偶数)
- 得到答案:总方案数 - 不合法方案数
代码
#include <bits/stdc++.h>
using namespace std;
const int MOD = 998244353;
const int N_MAX = 305;
const int S_MAX = 90005;
int a[N_MAX];
int f[S_MAX];
int g[S_MAX];
inline int addmod(int x, int y) {
x += y;
if (x >= MOD) x -= MOD;
return x;
}
inline int submod(int x, int y) {
x -= y;
if (x < 0) x += MOD;
return x;
}
inline int mulmod(long long x, long long y) {
return (int)((x * y) % MOD);
}
int main() {
int n;
cin >> n;
int S = 0;
for (int i = 1; i <= n; ++i) {
cin >> a[i];
S += a[i];
}
// 初始化
memset(f, 0, sizeof(f));
memset(g, 0, sizeof(g));
f[0] = 1;
g[0] = 1;
long long pow3 = 1;
// 计算至少装满和恰好装满的DP
for (int i = 1; i <= n; ++i) {
int v = a[i];
pow3 = mulmod(pow3, 3);
// 至少装满DP: f[j]表示红色和至少为j的方案数
// 每个数有三种选择:红(贡献v)、绿(不贡献)、蓝(不贡献)
// 所以转移为:f[j] = 2 * f[j] + f[j - v]
for (int j = S; j >= 0; --j) {
f[j] = mulmod(2, f[j]);
if (j >= v) {
f[j] = addmod(f[j], f[j - v]);
}
}
// 恰好装满DP: g[j]表示红色和恰好为j的方案数
for (int j = S; j >= v; --j) {
g[j] = addmod(g[j], g[j - v]);
}
}
// 计算不合法方案数
int half = (S + 1) / 2;
long long bad = 0;
for (int j = half; j <= S; ++j) {
bad = addmod(bad, f[j]);
}
bad = mulmod(bad, 3); // 三种颜色对称
// 如果S是偶数,需要减去重复计算的部分
if (S % 2 == 0) {
long long overlap = g[S / 2];
overlap = mulmod(overlap, 3); // 三种颜色对称
bad = submod(bad, overlap);
}
long long ans = submod(pow3, bad);
cout << ans;
return 0;
}
留下点什么再走吧(只要别踩)




















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








