
📐 1. 线性相关性基础概念回顾
-
线性相关 (Linearly Dependent): 如果一个向量组中至少有一个向量可以被组内其他向量线性表示,那么这个向量组是线性相关的。
-
线性无关 (Linearly Independent): 如果向量组中的任何一个向量都不能被组内其他向量线性表示,那么这个向量组是线性无关的。
📚 2. 定理讲解
- 原无关加上β变相关,则β唯一表示
- 多出来的向量可以由少的向量组线性表示,即这些多出来的向量是冗余的,可以表示为其他向量的线性组合。那么这个多的向量组一定是线性相关的。
- 相关Ak=0(k≠0) |A|=0 r<m
- 部分相关整体相关,整体无关部分无关
- 原无关延长无关,相关缩短相关
- 非0向量之间正交必然无关,
- 0和任何正交,相关
定理 1 (整体与部分)
向量组与其**子集(部分)或超集(整体)**之间线性相关性的关系,这是最常用的判定规则。
-
Part 1 (部分相关 ⇒ 整体相关):
若 α,β 线性相关,则 α,β,γ 必线性 相关。
-
解释: 如果一个向量组的部分(子集)已经线性相关了,意味着子集中的某个向量可以被子集中的其他向量表示。将这个子集放入一个更大的整体(超集)后,这个表示关系依然成立,所以整个超集当然也是线性相关的。
-
-
Part 2 (整体无关 ⇒ 部分无关):
若 α,β,γ 线性无关,则 α,β 必线性 无关。
-
解释: 如果一个向量组的整体(超集)是线性无关的,这意味着整体中的任何一个向量都不能被其他向量线性表示。那么取它的任何部分(子集),子集中的向量之间自然也不可能存在线性表示关系,所以这个子集也是线性无关的。
-
定理 2 (分块向量组:局部与整体的关系)

习题










定理3(以少表多,多的相关)



非0向量之间正交必然无关,

习题
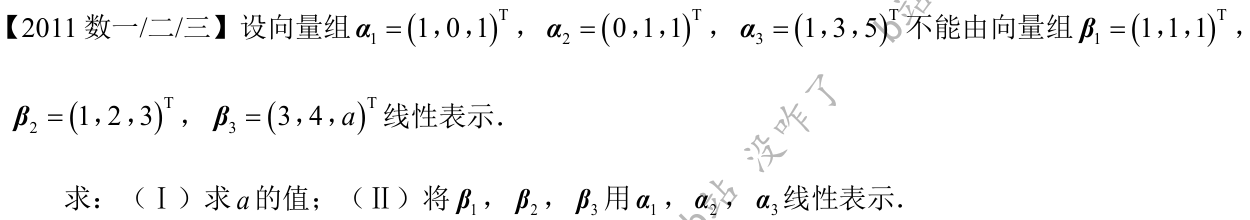


p1p2p3用a1a2a3表示:

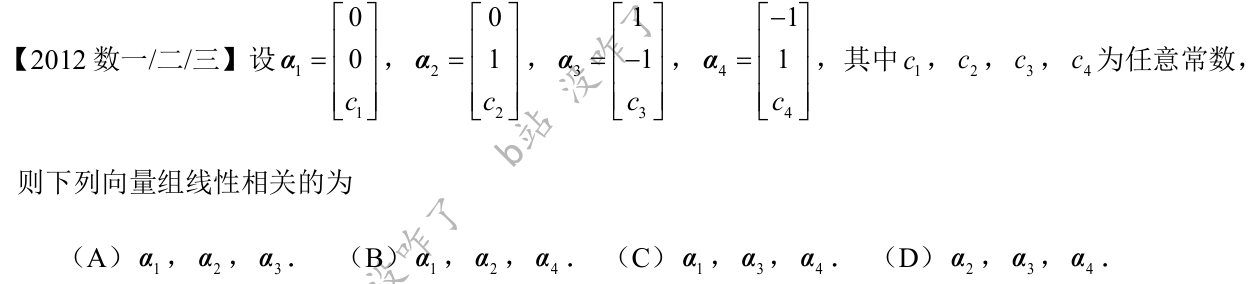
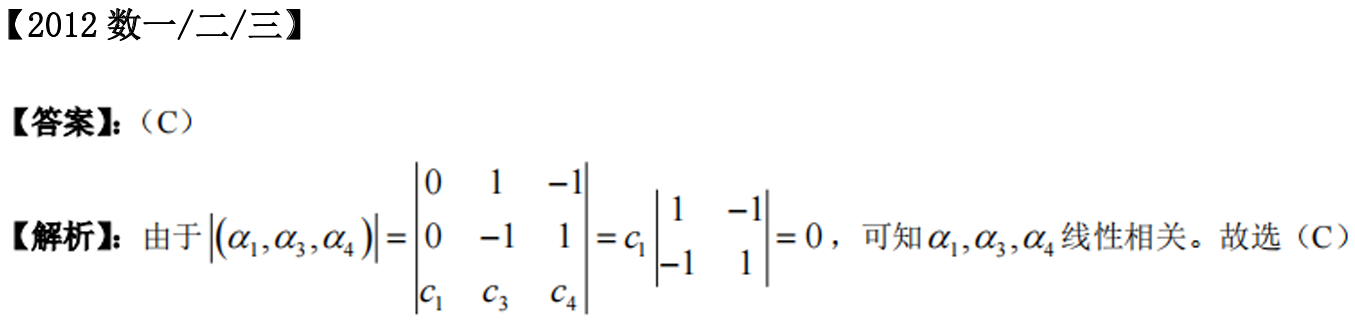




























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








